Second- Order and Wide-Sense Stationary Process

SECOND-ORDER AND WIDE-SENSE STATIONARY PROCESS

(a) Second-order stationary process

A process is said to be second order stationary, if the 2^nd order density function satisfies.

eeeeeeeeeee

(b) "A random process X (t) is said to be wide-sense stationary if it satisfies the conditions

(i) E [X (t)] = constant

(ii) R (t₁, t₂) = E [X(t₁) X(t₂)] = R(t₁ - t₂)

Note: All SSS process is a WSS process but the converse is not true. i.e., Every WSS process need not be a SSS process.

(c) Jointly Wide-Sense stationary processes :

Two random processes X (t) and Y (t) are called jointly wide-sense stationary if

(i) X(t) is a WSS process

(ii) Y(t) is a WSS process

(iii) R(t₁, t₂) = E[X(t₁) Y(t₂)] = R(t₁ - t₂)

(d) N-th order stationary.

The stationary concept can be defined by considering any number of random variables of the process.

Definition : Stationary to order N.

In general, a process is stationary to order N, if for N random variables of the process considered at times t₁, t₂, ... t_N, their N-th order joint density function is invariant with time origin shift.

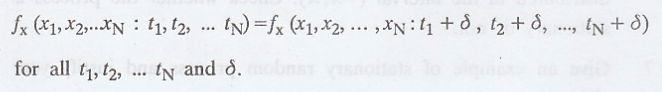
Comparison of SSS and WSS processes :

Note :

1. A second-order stationary process is also a first order-stationary.

2. The second-order densities of a SSS process are functions τ = t₁ - t₂

Theorem.

If a random process X(t) is WSS then it must also be covariance stationary. [AU 2003]

Proof :

Given: X (t) is WSS

(i) E[X(t)] = µ = a constant.

(ii) R(t₁, t₂) = a function of (t₁ - t₂)

The autocovariance function is given by

which depends only on the time difference.

Hence, X (t) is covariance stationary.

I. Example for Stationary of second order

Example 3.3.1

A random process is described by X(t) = A sin t + B cos t where A and B are independent random variables with zero mean and equal variances (or equal S.D). Show that the process is stationary of second order.

Solution:

Given: X (t) = A sin t + B cos t ........(1)

E[A] = 0, E[B] = 0 ...........(2)

Hence, the process X (t) is stationary of second order.

II. Example for WSS process [Uniform distribution type]

Example 3.3.2

Show that the random process X (t) = A cos (ωt + θ) is wide sense stationary it A & ω are constant and 'θ' is uniformly distributed random variable in (0, 2л). [A.U. N/D, 2003, 2005] [A.U. M/J 2007] [A.U Trichy A/M 2010] [A.U A/M 2010] [A.U CBT Dec. 2009] [A.U Tvli A/M 2009] [A.U N/D 2011, A/M 2014, N/D 2015 R-8, N/D 2015 R-13] [A.U M/J 2016 R13 RP] [A.U N/D 2017 (RP) R-13] [A.U A/M 2018 (R13, R08)] [A.U A/M 2019 (RP) R-13]

Solution :

Given X(t) = A cos (ωt + θ),

where 'θ' is uniformly distributed in (0, 2л).

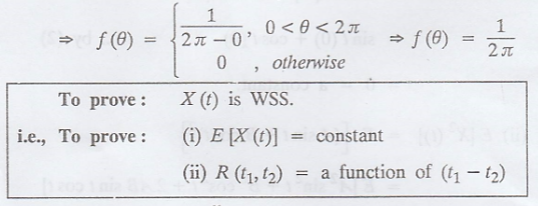
Proof :

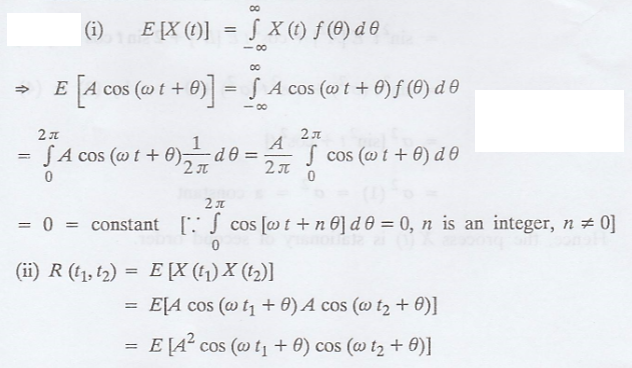
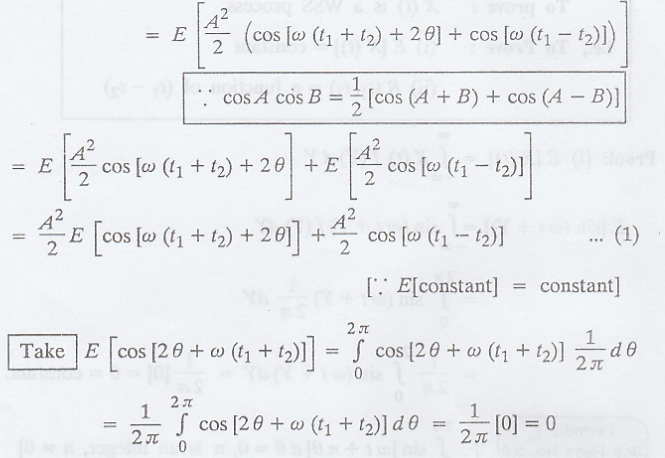
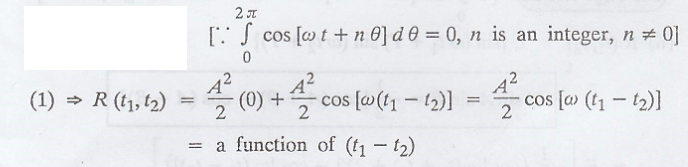
Hence, X (t) is a WSS process.

Example 3.3.3

If X (t) = sin (ωt+ Y), where Y is uniformly distributed in (0, 2π), then show that X (t) is wide-sense stationary.[AU N/D 2018 R13 RP] [A.U N/D 2009] [A.U Trichy M/J 2011] [A.U N/D 2017 R-08] [A.U A/M 2019 R-13 PQT]

Solution:

Given: X (t) = sin (ωt + Y), where 'Y' is uniformly distributed in (0, 2л)

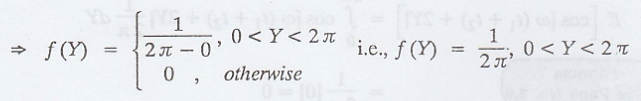
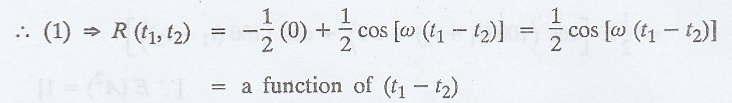
=> The autocorrelation function is a function of time difference only.

.’. X(t) is a WSS process.

Example 3.3.4

Consider the random process X(t) = A cos (100 t + θ), where A and θ are independent variables. A is a random variable with mean 0 and variance 1. θ is uniformly distributed in [-л, л]. Find mean and auto correlation and hence show that X(t) is WSS.

Solution:

Given: X(t) = A cos (100 t + θ)

E [A] = 0, Var(A) = 1 ............(1)

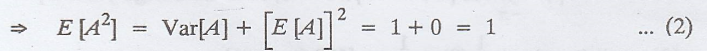
Here, 'θ' is uniformly distributed in [-л, л]

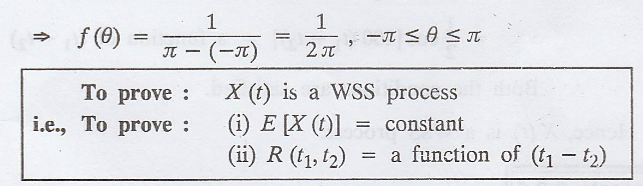
Proof :

Both the conditions are satisfied.

Hence, X (t) is a WSS process.

Example 3.3.5

Consider a random process Y(t) = X(t) cos (ω_ot + θ), where X(t) is wide sense stationary random process. θ is a random variable independent of X(t) and is distributed uniformly in (-л, л) and ω_o is a constant. Prove that Y(t) is wide-sense stationary. [A.U A/M 2003] [A.U M/J 2016 R-13 PQT]

Solution:

Given: X(t) is a WSS process.

E [X(t)] = constant.

R (t₁, t₂) = a function of (t₁ - t₂)

 

i.e., R [t₁, t₂] = E(X(t₁) X(t₂)] = a function of (t₁ - t₂) ......(1)

Given: Y(t) = X(t) cos (ω_ot + θ),

where 'θ' is uniformly distributed in (-л, л)

Proof :

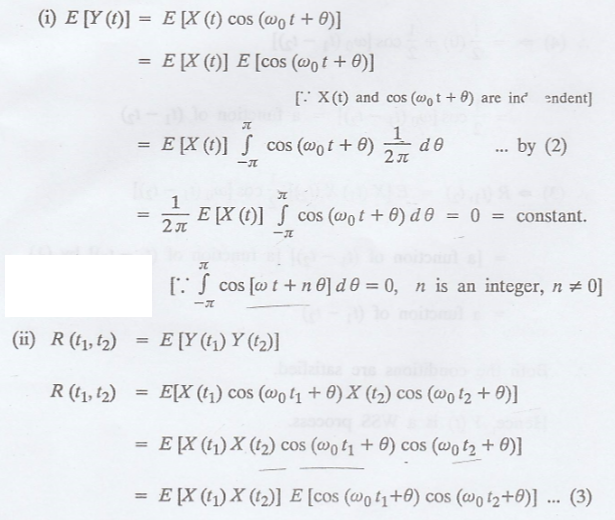
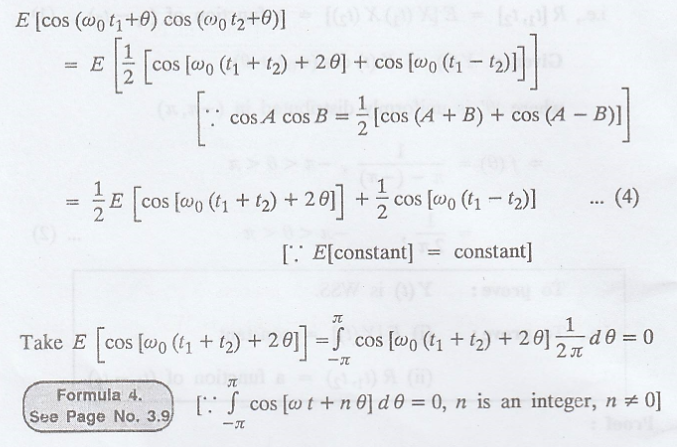
Both the conditions are satisfied.

Hence, Y(t) is a WSS process.

III. Example for not WSS process [Uniform distribution type]

Example 3.3.6

For a random process X(t) = Y sin ω t, Y is an uniform random variable in the interval -1 to +1. Check whether the process is wide sense stationary or not. [A.U N/D 2006, Trichy M/J 2011]

(OR) Verify whether the sine wave random process X (t) = Y sin ω t, Y is uniformly distributed in the interval -1 to 1 is WSS or not.

Solution:

Given: X (t) Y sin ωt,

where 'Y is uniformly distributed in -1 to 1.

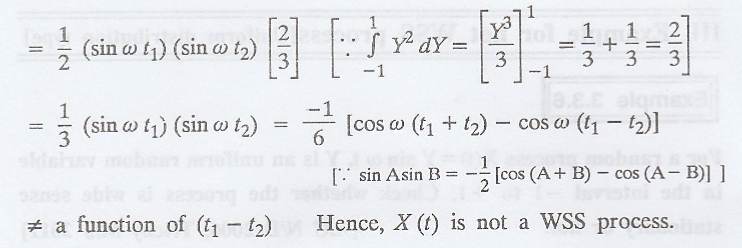
Example 3.3.7

A random process X(t) is defined as X(t) = A cos (ωt+ θ), where ω and θ are constants and A is a random variable. Determine whether X(t) is a wide sense stationary process or not. [A.U Tvli A/M 2009]

Solution:

Given: X(t) = A cos (ωt+ θ), A is a random variable.

Example 3.3.8

Verify whether the random process X(t) = A cos (ω_ot + φ) is a WSS process where φ is uniformly distributed random variable in (0, л).

Solution:

Given: X (t) = A cos (ω_ot+φ),

where 'φ' is uniformly distributed in (0, л).

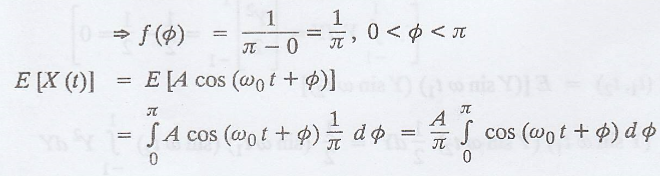
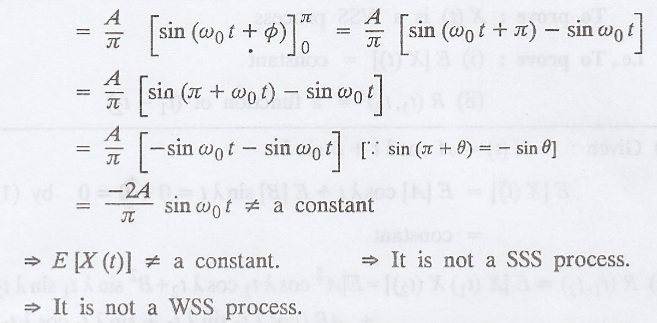
IV. Example for WSS process [Normal distribution type]

Example 3.3.9

If X(t) = A cos λt + B sin λt, where A and B are two independent normal random variables with E(A) = E(B) = 0, E(A²) = E(B²) = σ², and λ is a constant, prove that {X(t)} is a strict sense stationary process of order 2.

[OR] If X (t) = A cos λt + B sin λ t, t ≥ 0 is a random process where A and B are independent N (0, σ²) random variables, examine the WSS process of X(t). [OR] Show that the random process X (t) = A cos λ t + B sin λt is WSS if A and B are random variables such that E(A) = E(B) = 0, E(A²) = E(B²) and E[AB] = 0 [A.U. N/D 2006, M/J 2007, N/D 2007, Trichy M/J 2011] [A.U CBT A/M 2011, CBT N/D 2011, Tvli M/J 2011] [A.U M/J 2013, A/M 2015 R8, A/M 2015 (RP) R8, R13] [A.U N/D 2017 (RP) R8] [A.U N/D 2018 R-13 PQT]

Solution :

Given: E[A] = 0, E[B] = 0 .................(1)

E[AB] = E[A] E[B] = (0) (0) = 0 .................(2)

['.' A and B are independent]

E[A²] = E[B²] = σ² = k .................(3)

Example 3.3.10

Given a random variable y with characteristic function φ(ω)=E[e^iωy] and a random process defined by X(t)= cos [λt+y], show that {X(t)} is stationary in the wide sense of φ(1) = φ(2) = 0. [A.U. A/M. 2003] [A.U A/M 2005] [A.U M/J 2009] [A.U CBT Dec. 2009]

Solution :

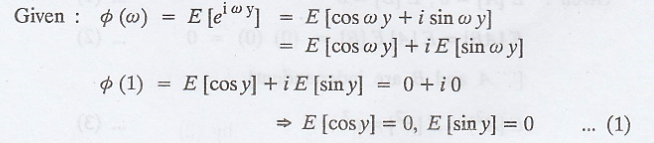
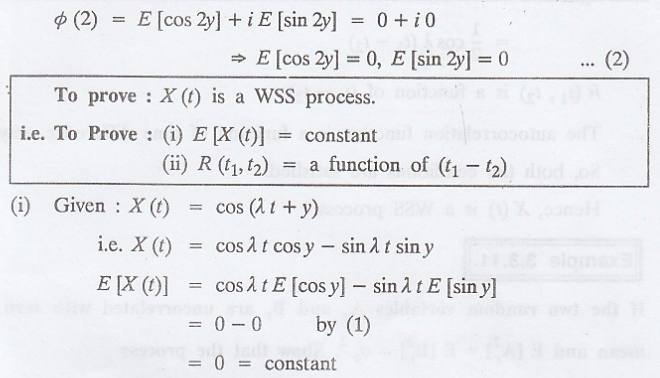
Proof:

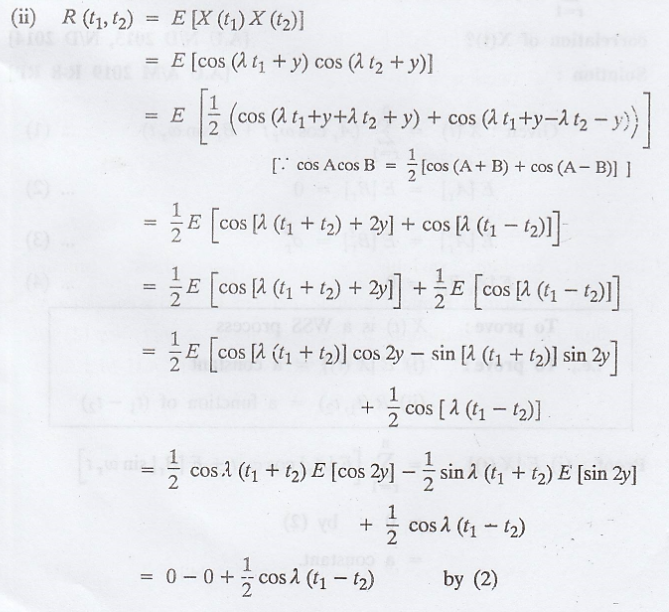
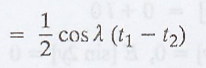
R (t₁, t₂) is a function of (t₁ - t₂)

The autocorrelation function is a function of time difference only.

So, both the conditions are satisfied.

Hence, X(t) is a WSS process.

Example 3.3.11.

If the two random variables Ar and Br are uncorrelated with zero mean and 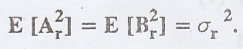 Show that the process 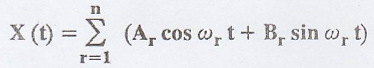 is WSS. What are mean and auto correlation of X(t)? [A.U N/D 2013, N/D 2014] [A.U A/M 2019 R-8 RP]

Solution :

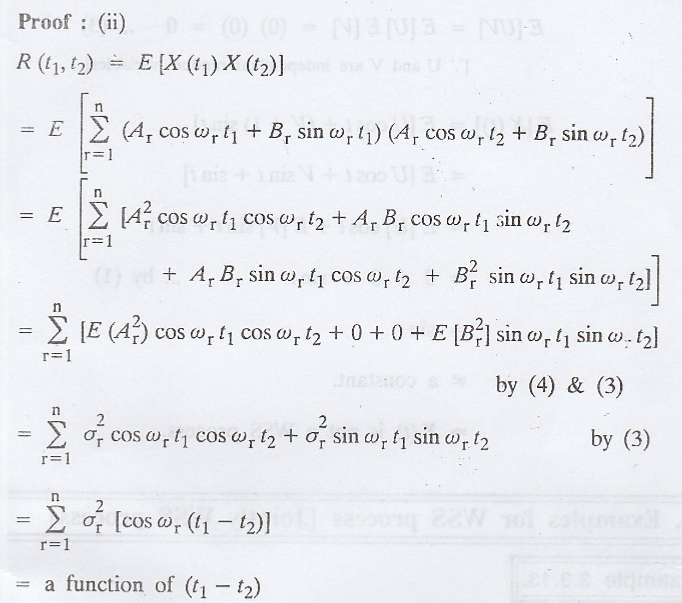
.'. Both the conditions are satisfied.

Hence, X (t) is a WSS process.

V. Example for not WSS Process [Normal distribution type]

Example 3.3.12.

Consider a random process X(t) defined by X(t) = U cost + (V+1) sin t, where U and V are independent random variables for which E[U] = E[V] = 0, E[U²] = E[V²] = 1. Is X(t) is WSS? Explain your answer.[AU A/M. 2008]

Solution:

Given: X(t) = U cost + (V+1) sint,

E[U] = E[V] = 0 ..................(1)

E[U²] = E[V²] = 1 ..................(2)

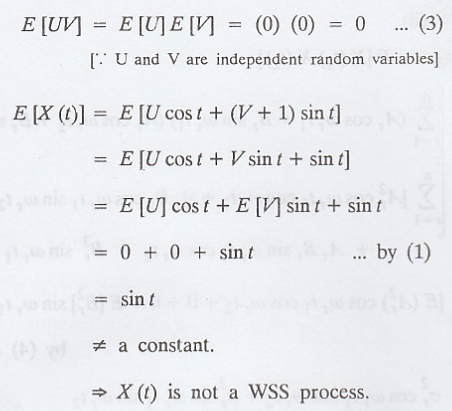
VI. Examples for WSS process [Jointly WSS process]

Example 3.3.13.

Two random process X(t) and Y(t) are defined by X(t) = A cos ωt + B sin ωt and Y(t) = B cos ωt- A sin ωt. Show that X(t) and Y(t) are jointly wide-sense stationary, if A and B uncorrelated random variables with zero means and the same variances and ω is constant. [A.U. A/M 2003] [A.U. Model] [A.U CBT N/D 2010] [A.U A/M 2014] [A.U N/D 2018 R-13 RP]

[OR] Let the two random processes X (t) and Y(t) be defined as X(t) = A cos ωt+ B sin ωt, Y(t) = B cos ωt - A sin ωt, where A and B are random variables, ω is a constant. If E[A] = E[B] = 0, E[AB] = 0 and E[A²] = E[B²] = k, prove that X(t) and Y(t) are jointly wide-sense stationary.

Solution:

Given:

X(t) = A cos ωt + B sin ωt

Y(t) = B cos ωt - A sin ωt

.'. Both the conditions are satisfied.

{X(t)} and {Y(t)} are jointly WSS process.

Example 3.3.14

If X(t) = 5 cos (10t + θ) and Y(t) = 20 sin (10t + θ), where θ is a random variable uniformly distributed in (0, 2л), prove that the process {X(t)} and {Y(t)} are jointly wide-sense stationary.

Solution:

Given: X(t) = 5 cos (10t + θ)

Y(t) = 20 sin (10t + θ)

where 'θ' is uniformly distributed in (0, 2л)

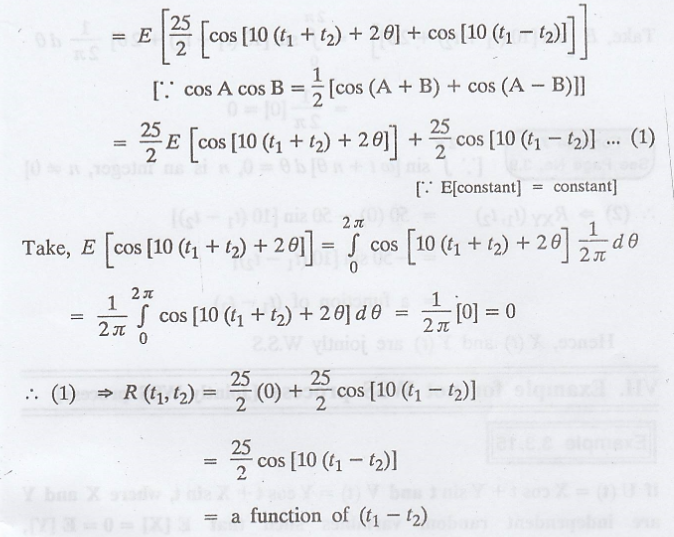
.'. Both the conditions are satisfied.

Hence, X (t) is a WSS process.

Similarly, Y(t) is a WSS process.

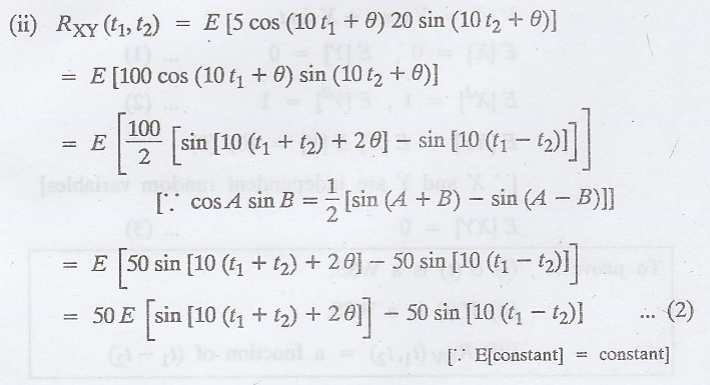
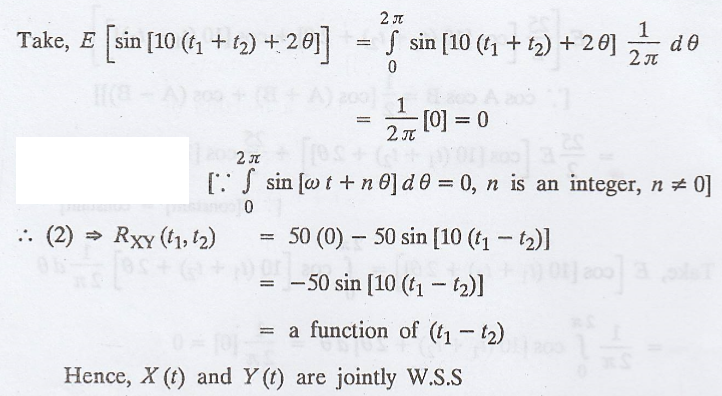
VII. Example for not WSS process [Jointly WSS process]

Example 3.3.15

If U(t) = X cost + Y sint and V(t) = Y cos t + X sin t, where X and Y are independent random variables such that E[X] = 0 = E[Y], E[X²] = E[Y²] = 1, show that {U(t)} and {V(t)} are individually stationary in the wide-sense, but they are not jointly wide-sense stationary.

Solution:

Given: U(t) = X cos t + Y sin t

V(t)  = Y cos t + X sin t

E[X] = 0, E[Y] = 0 ..............(1)

E[X²] = 1, E[Y²] = 1 ..............(2)

E[XY] = E[X] E[Y] = (0) (0) [ X and Y are independent random variables]

E [XY] = 0 ..............(3)

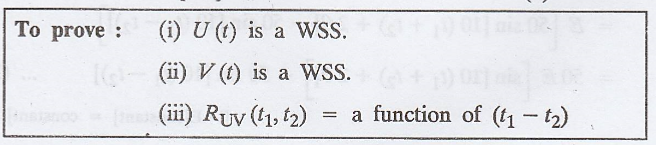
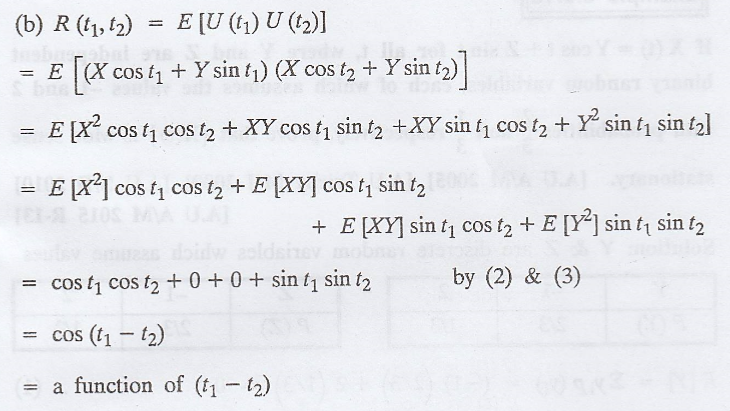
= a function of (t₁ - t₂)

(Hence, U(t) is a WSS process.

(ii) Similarly, V(t) is a WSS process.

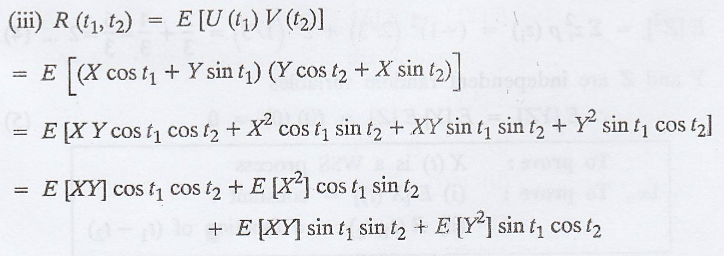
Hence, U(t) and V(t) are individually WSS process, but not jointly WSS process.

VIII. Example for WSS process[Discretre random variable type]

Example 3.3.16

If X(t) = Y cos t + Z sin t for all t, where Y and Z are independent binary random variables, each of which assumes the values -1 and 2 with probabilities 2/3 and 1/3 respectively, prove that {X(t)} is wide sense stationary. [A.U A/M 2005] [A.U Trichy M/J 2009] [A.U N/D 2010] [A.U A/M 2015 R-13]

Solution:

Y & Z are discrete random variables which assume values

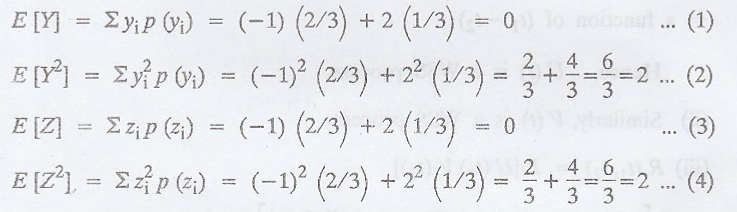
Y and Z are independent random variables

Example 3.3.17

Assume a random process X(t) with sample functions X(t, s₁) = cos t, X(t, s₂) = - cos t, X(t, s₃) = sin t, X (t, s₄) = -sin t which are equally likely, show that X(t) is WSS process. [A.U N/D 2017 R-08]

Solution :

Given: P[X(t, S₁)] = P[X(t, s₂)] = P[X(t, S₃)] = P[X(t, S₄)] = 1/4

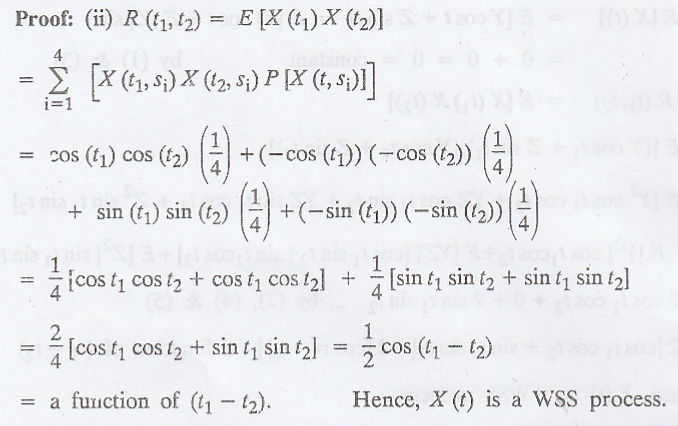
IX. Example for not WSS process [discrete random variable type]

Example 3.3.18

A random process X(t) is characterized by four sample functions (i) X(t, s₁) = -1, (ii) X(t, s₂) = -2, (iii) X (t, s₃) = 3, (iv) X(t, S₄) = t. Assume that the sample functions are equally likely. Find the auto-correlation function and check whether it is WSS process or not.

Solution :

Given: P[X(t, s1)] = P[X(t, s2)] = P[X(t, s3)] = P[X(t, s4)] = 1/4

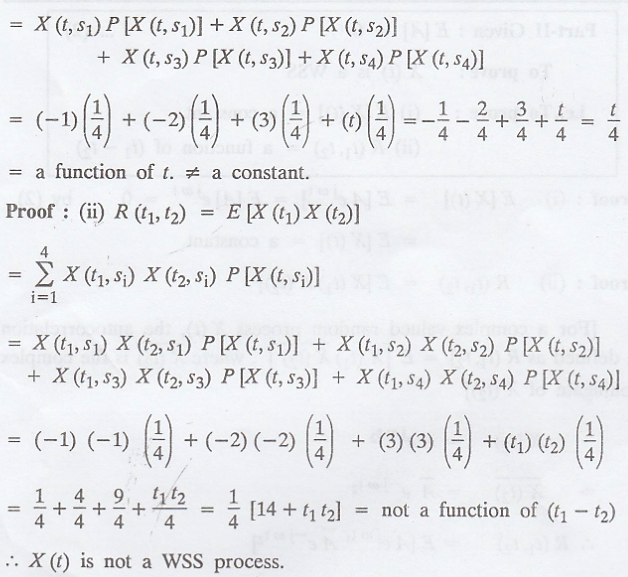
X. Example for WSS process [Complex valued type]

Example 3.3.19

Show that the random process X(t) = A e ^{j ω t} is WSS if and only if E[A] = 0

Solution :

Proof :  

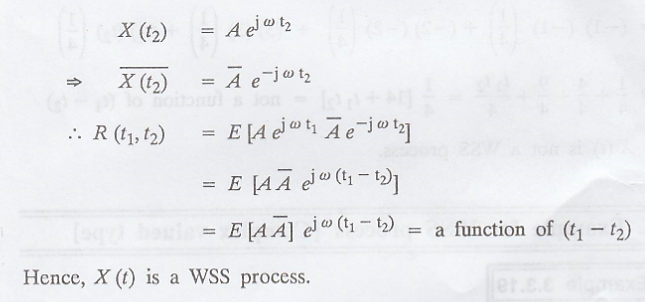
EXERCISE 3.3

1. If X(t) = Y cos ωt + Z sin ωt where Y and Z are two independent normal random variables with E[Y] = E[Z] = 0, E[Y²] = E[Z²] = σ² and ω is a constant. Prove that X(t) is a SSS of order 2. [A.U A/M 2015 (RP) R8]

2. Show that the random process X(t) = A sin (ωt + φ), where A and ω are constants, φ is a random variable uniformly distributed in (0, 2л) is WSS.

3. Show that the random process X(t) = 100 sin (ωt + φ) is WSS, where ω is a constant and φ is uniformly distributed in (0, 2л)

4. If X(t) = cos (λt + y) where y is uniformly distributed random variable in (-л, л). Show that X (t) is WSS.

5. If X (t) = U cos t + V sin t where U and V are independent random variables each of which assumes the values -2 and 1 with probabilities 1/3 and 2/3 respectively. Show that X(t) is covariance stationary (WSS). [A.U N/D 2015 R8]

6. Show that the random process X(t) = A cos t + B sin t, -∞ < t < ∞, is a WSS process, where A and B are independent random variables each of which has a value -2 with probability 1/3 and a value 1 with probability 2/3 [AU A/M. 2011] [A.U N/D 2015 R13 RP]

7. Let X(t) = Y cos t + Z sin t for all t, where Y and Z are independent binary random variables each of which assumes the values -1 and 1 which are equally likely, then prove that X(t) is WSS. [A.U. Tvli. M/J 2011]

8. Consider a random process X(t) = A cos(50t + φ), where A and φ are independent random variables. A is a random variable with zero mean and variance 1. φ is uniformly distributed in (-л, л) show that X (t) is WSS. [A.U. A/M 2004]

9. If X(t) = 2 cos (5t + θ), Y(t) = 5 cos (5 t + θ), where is θ a random variable uniformly distributed in (0, 2л), prove that the process X(t) and Y(t) are jointly WSS.

10. Consider a random process Z(t) = X₁ cos ω_ot - X₂ sin ω_ot, where X₁ and X₂ are independent Gaussian random variables with zero mean and variance σ². Find E[Z] and E[Z²]

11. The random process X(t) = sin(ωt + y), where y is a random variable uniformly distributed in (0, 2л). Prove that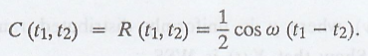 

12. If X(t) = R cos (ωt + φ) where R and φ are independent random variables with E[R] = 2 and V(R) = 6 and φ is uniformly distributed in (-л, л). Рrove that X(t) is WSS process.

13. Consider the random process X(t) = cos (t + φ) where φ is a random variable with density function f(φ) = 1/π, -π/2 < φ < π/2, check whether or not the process is wide-sense stationary. [A.U. N/D 2010]

14. Let X(t) be a WSS process with auto correlation RXX(τ) = A e ^{– α | τ |}. Find the second moment of the random variable Y = X(5) - X(2).