Random Process and Linear Algebra: Unit I: Probability and Random Variables,,
Sample spaces having equally likely outcomes
Problems of Type P(A) = n(A)/n(S)
If we assume that all outcomes of an experiment are equally likely to occur, then the probability of any event E equals the proportion of outcomes in the sample space that are contained in E. P (E) = number of points in E / number of points in S
Sample spaces having equally likely outcomes.
If we assume that all outcomes of an
experiment are equally likely to occur, then the probability of any event E
equals the proportion of outcomes in the sample space that are contained in E.
P (E) = number of points in E / number
of points in S
TYPE 1(a) P(A) = n(A)/n(S)
Example 1.1.1
Find the probability that exactly one
head appears in a single throw of a fair coin.
Solution:
Formula P(A) = n(A)/n(S)
Here A be the event of getting exactly
one head in a single throw of a fair coin.
S --> Sample space = {H, T}
n(S) = 2
n(A) = 1
.'. P(A) = n(A)/n(S) = 1/2
Example 1.1.2
If two dice are rolled, what is the
probability that the sum of the upturned faces will be equal to 7?
Solution :
The number of total outcomes is n(S) =
36
Let A = {Sum of the upturned faces will
equal 7} = {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}
n(A) = 6
It is assumed that all the 36 possible
outcomes are equally likely.
.'. P(A) = n(A)/n(S) = 6/36 = 1/6
Example 1.1.3
From a pack of 52 cards two cards are
drawn the first being replaced before the second is drawn. Find the probability
that the first one is a diamond and second is a king.
Solution:
Let A be an event of drawing a diamond.
P (A) = n(A)/n(S) = 13/52 = 1/4
Let B be an event of drawing a king.
P(B) = n(B)/n(S) = 4/52 = 1/13
A and B are independent events.
Hence P (A ∩ B) = P(A).P(B) = (1/4)
(1/13) = 1/52
Example 1.1.4
A bag contains 5 white and 10 red balls.
Three balls are taken out at random. Find the probability that all the three
balls drawn red.
Solution :
Total number of balls = 15
S = {Three balls are taken out of 15}
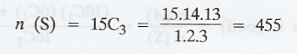
Number of red balls = 10
A = {Three balls which are red}
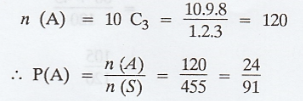
Example 1.1.5
If 3 balls are "randomly
drawn" from a bowl containing 6 white and 5 black balls, what is the
probability that one of the drawn balls is white and the other two black ?
Solution :
The total number of balls = 11
Among this 3 balls are randomly selected
from the bowl.
.'. Total number of possible outcomes =
n(S) = 11C3 = 11.10.9 / 1.2.3 = 165
The number of favourable outcomes
(i.e., 1 is white and the other two are
black) = n(A) = 6C1 x 5C2
= 6 x (5.4/1.2) = 6 x 10 = 60
Hence the required probability P(A) =
n(A)/n(S) = 60/165 = 4/11
Example 1.1.6
A lot of integrated circuit chips consists of 10 good, 4 with minor defects and 2 with major defects. Two chips are randomly chosen from the lot. What is the probability that atleast one chip is good? [A.U M/J 2017]
Solution :
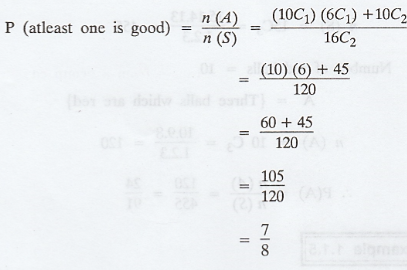
Example 1.1.7
A committee of 5 persons is to be
selected randomly from a group of 5 men and 10 women. (a) Find the probability
that the committee consists of 2 men and 3 women. (b) Find the probability that
the committee consists of all women.
Solution :
(a) The number of total outcomes is
given by n(S) = 15C5
It is assumed that "random
selection" means that each of the outcomes is equally likely.
Let A = {The committee consists of 2 men
and 3 women}
Then n(A) = (5C2) (10C3)
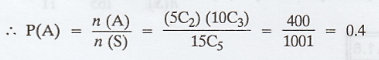
(b) Let B = {the event that the
committee consists of all women}
n(B) = (5C0) (10C5)
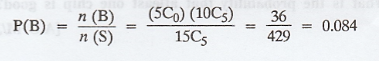
Example 1.1.8
Four persons are chosen at random from a
group containing 3 men, 2 women and 4 children. Show that the chance that
exactly two of them will be children is 10/21. [A.U N/D 2006]
Solution :
Total number of persons = 9
4 persons can be chosen out of 9 persons
9C4 ways = 9.8.7.6 / 1.2.3.4 = 126 ways
The number of ways of choosing 2
children out of 4 children = 4C2 ways = 4.3 / 1.2 = 6 ways
The remaining two persons can be choosen
from 5 persons (3 men + 2 women) = 5C2 ways
= 5.4 / 1.2 = 10 ways
.'. The number of favourable case = 4C2
× 5C2 ways = 6 × 10 ways = 60 ways.
Required probability = 60/126 = 10/21
Example 1.1.9
Four persons are chosen at random from a
group containing 3 men, 2 women and 4 children. Show that the chance that
exactly two of them will be children is 10/21. [A.U N/D 2006]
Solution :
Total number of persons = 9
4 persons can be chosen out of 9 persons
= 9C4 ways = 9.8.7.6 / 1.2.3.4 = 126 ways
The number of ways of choosing 2
children out of 4 children = 4C2 ways = 4.3 / 1.2 = 6 ways
The remaining two persons can be choosen
from 5 persons (3 men + 2 women) = 5C2 ways = 5.4 / 1.2 = 10 ways
.'. The number of favourable case = 4C2
× 5C2 ways = 6 × 10 ways = 60 ways.
.'. Required probability = 60/126 =
10/21
Example 1.1.10
Two dice are thrown together. Find the
probability that (a) the total of the numbers on the top face is 9 and (b) the
top faces are same. [A.U. M/J 2006]
Solution :
(a) Let A be the event which gives the
sum of the top numbers as 9.
Favourable cases which gives the total
as 9 are (3, 6), (4, 5), (5, 4), (6, 3)
P(A) = 4/36 = 1/9
(b) Let B be the event which gives the
top faces are same.
Favourable cases are (1, 1), (2, 2), (3,
3), (4, 4), (5, 5) and (6, 6)
P(B) = 6/36 = 1/6
Example 1.1.11
Out of (2n + 1) tickets consecutively
numbered three are drawn at random. Find the probability that the numbers on
them are in arithmetic progression. [A.U. M/J 2006]
Solution:
Out of (2n + 1) tickets, 3 tickets can
be drawn in (2n+1)C3 ways.
.'. total number of exhaustive cases
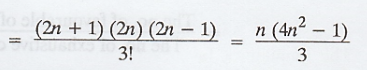
To find the favourable number of cases,
we give all possibilities in which the numbers on the drawn tickets are in A.P.
with common difference d = 1, 2, 3, ..., n-1, n (say)
If d = 1, the possibilities are
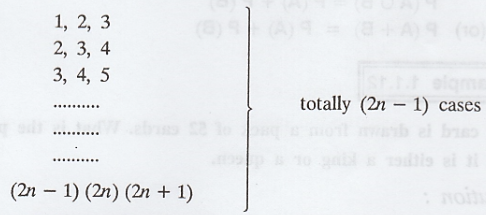
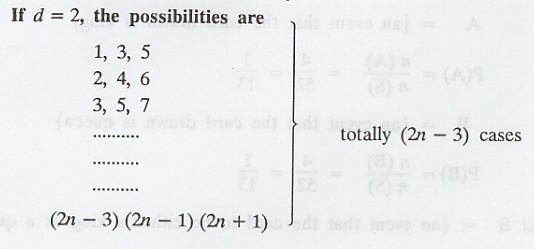
Similary, if d = n 1, then the possible
cases are
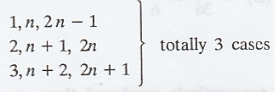
If d= n, then there is only one case as
(1, n + 1, 2n + 1)
.'. the total number of favourable cases
is (2n-1) + (2n-3) + ... + 5 + 3+1 which is an A.P. with common difference 2.
Hence favourable cases = 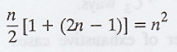
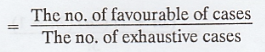
Thus the required probability = 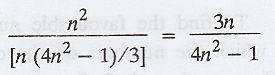
Random Process and Linear Algebra: Unit I: Probability and Random Variables,, : Tag: : Problems of Type P(A) = n(A)/n(S) - Sample spaces having equally likely outcomes
Related Topics
Related Subjects
Random Process and Linear Algebra
MA3355 - M3 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
