Signals and Systems: Unit IV: Analysis of Discrete Time Signals,,
Relationship between Z Transform and DIFT
Inverse z Transform Using Contour Integration
Inverse z Transform Using Contour Integration Steps to calculate inverse z transform using contour integration.
Inverse z Transform Using Contour Integration
Steps to calculate
inverse z transform using contour integration.
I Step:
Define the function X0(z). X0(z) is rational
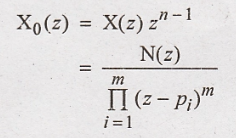
Here
m ⇒ order of the pole
II Step:
(i) If order of the pole is m = 1, residue of X0(z) at pole Pi is
gives
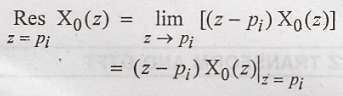
(ii)
If order of the pole is m = 2, residue of X(z) can be calculated as
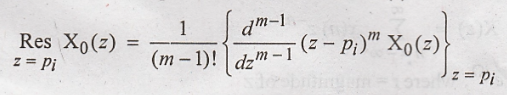
III Step:
By using residue theorem, calculate x(n) for poles inside the unit circle
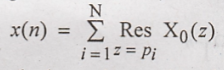
(ii)
To calculate poles outside of contour integration
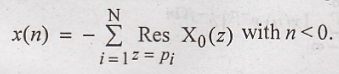
Problem 1:
Find
the inverse z transform using contour integral method.
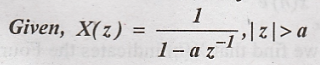
Solution:
I Step:
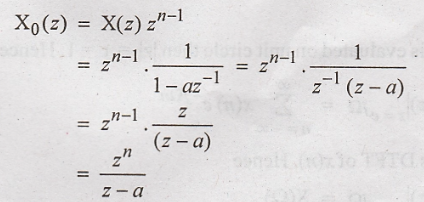
Hence
the order of pole (m = 1)
II step:
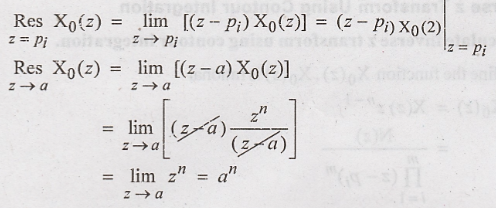
III Step:
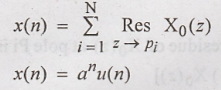
RELATIONSHIP BETWEEN Z TRANSFORM AND DTFT
z
transform of discrete time signal is given as
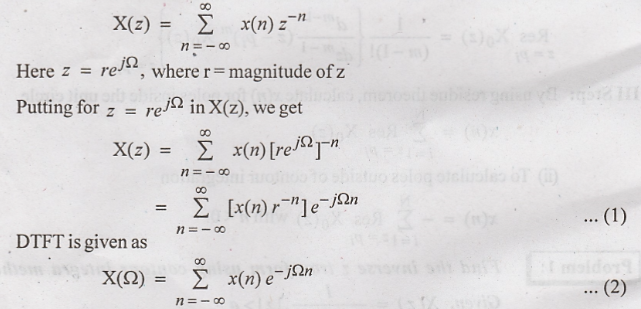
By
comparing (1) & (2), we find that X(z) indicates the Fourier transform of x(n)r-n.
If
X(z) of (1) is evaluated on unit circle then [z] = r = 1. Hence
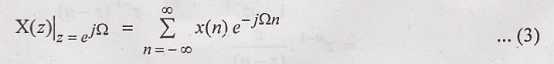
R.H.S
of (3) is DTFT of x(n). Hence
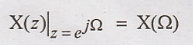
Signals and Systems: Unit IV: Analysis of Discrete Time Signals,, : Tag: : Inverse z Transform Using Contour Integration - Relationship between Z Transform and DIFT
Related Topics
Related Subjects
Signals and Systems
EC3354 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
