Regression

REGRESSION

i. Regression

Regression is a mathematical measure of the average relationship between two or more variables in terms of the original limits of the data.

ii. Lines of regression

(a) The line of regression of y on x is given by

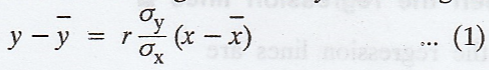
(b) The line of regression of x on y is given by

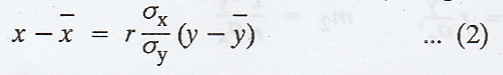
Note: Both the lines of regression passes through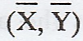 

iii. Regression coefficients

(a) Regression coefficient of y on x is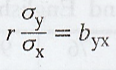 

(b) Regression coefficient of x on y is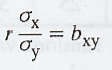 

Correlation coefficient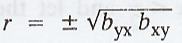 

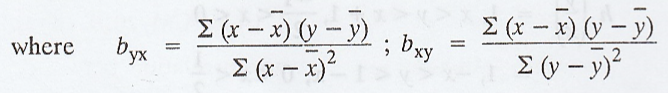
iv. Properties of Regression Lines

(a) The regression lines pass through  is the point of intersection of the regression lines.

(b) When r = 1, that is when there is a perfect, +ve correlation or when r = -1, that is when there is a perfect -ve correlation the equation (1) and (2) becomes one are the same and so the regression lines coincide

(c) When r = 0 the equations of the lines are y = ȳ and x =  which represent perpendicular lines which are parallel to the axis.

(d) The slopes of the lines are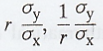 

Since the S.D's σ_x and σ_y are +ve, both the slopes are +ve if r is +ve and -ve if r is -ve. That is all the three, namely the two slopes and r are of same sign.

v. Angle between the regression lines

The slopes of the regression lines are

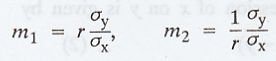
If is the angle between the lines, then

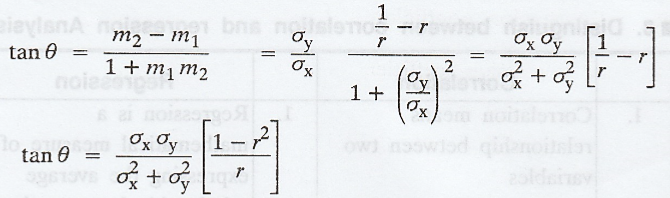
When will the two regression lines be (a) at right angles (b) Coincident? [A.U N/D 2012] [A.U A/M 2019 (R13) PQT]

Note: 1. When r = 0, that is, there is no correlation between x and y.

tan θ = ∞ (or) θ = π/2 and so the regression lines are perpendicular

2. When r 1 or -1, that is, when there is a perfect correlation, +ve or -ve, θ = 0 and so the lines coincide.

vi. Correlation coefficient is the geometric mean between the two regression coefficients

Proof :

We know that,

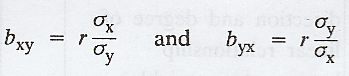
vii. If one of the regression coefficient is greater than unity the other must be less than unity.

Proof :

We know that, r² = b_xy b_yx ≤ 1 .............(1)

Assume that b_xy > 1

we have, to prove that b_yx < 1

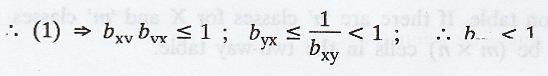
viii. Distinguish between correlation and regression Analysis

ix. Standard errors of estimate

The standard error of estimate of x is

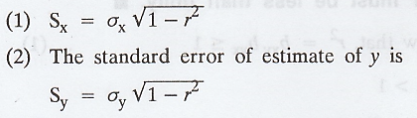
x. Correlation of Grouped data

When the number of observations is large and the variables are grouped, the data can be classified into two way frequency distribution called a correlation table. If there are 'n' classes for X and 'm' classes for Y, there will be (m x n) cells in the two-way table.

The formula for calculating the co-efficient of correlation is

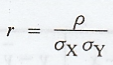
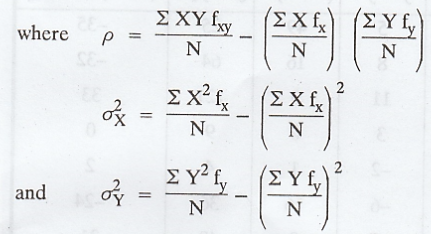
xi. Probable Error of correlation co-efficient

The probable error of correlation co-efficient is given by,

P.E. (r) = 0.6745 × S.E.

where S.E. is the standard error and is S.E. (r) = 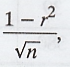where 'r' is the correlation co-efficient and 'n' is the number of observation.

Thus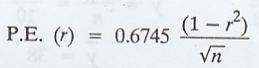 

The reason for taking the factor 0.6745 is that in a normal distribution, the range µ = ± 0.6745 covers 50% of the total area. This error enables us to find the limits within which correlation co-efficient can be expected to vary.

Example 2.3.1

From the following data, find (i) the two regression equations, (ii) the coefficient of correlation between the marks in Economics and statistics, (iii) the most likely marks in Statistics when marks in Economics are 30. [A.U M/J 2007]

Solution :

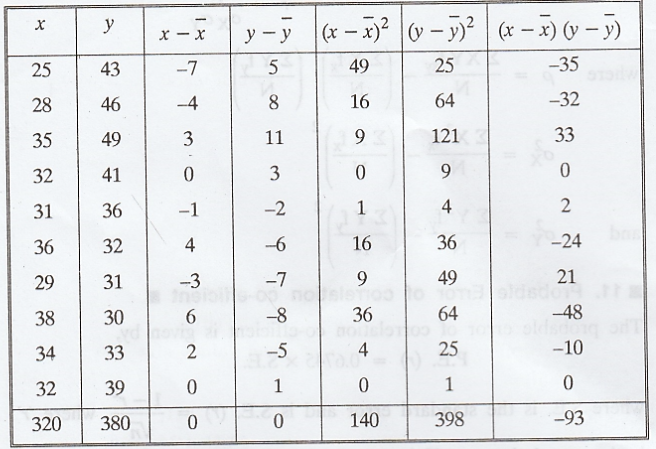
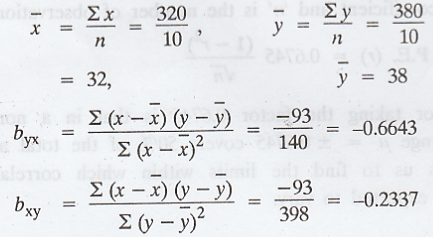
(i) Equation of the line of regression of x on y is

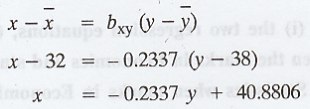
Equation of the line of regression of y on x is

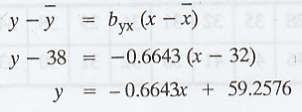
(ii) Co-efficient of correlation

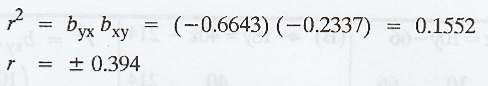
(iii) The most likely marks in statistics (y) when marks in Economics (x) are 30

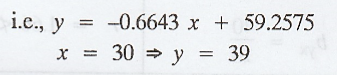
Example 2.3.2

The two lines of regression are

 The variance of x is 9. Find (i) The mean values of x and y (ii) Correlation co-efficient between x and y [AU N/D 2008] [A.U CBT M/J 2010, CBT N/D 2011, CBT A/M 2011] [A.U A/M 2015 (RP) R13] [A.U M/J 2015 R13 PQT] [A.U M/J 2016 R13 RP]

Solution :

(i) Since both the lines of regression passes through the mean values  and , the point  must satisfy the two regression lines

Hence the mean values are given by 

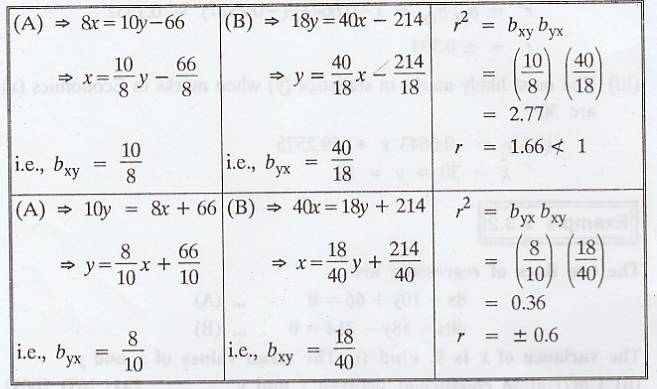
Since both the regression coefficients are positiver must be positive r = 0.6.

Example 2.3.3

The following table gives according to age x, the frequency of marks. obtained 'y' by 100 students in an intelligence test. Measure the degree of relationship between age and intelligence test.

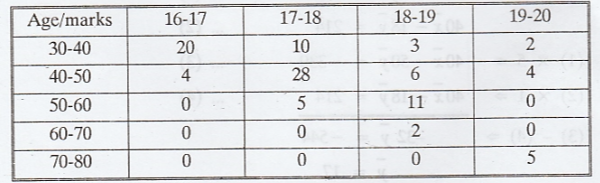
The origin is taken as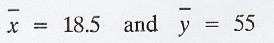 

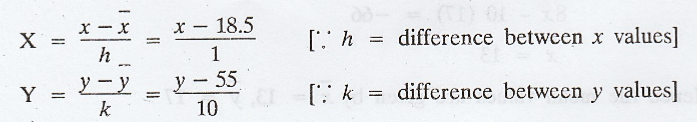
f_y -> sum of the each row

f_x -> sum of the each column

f_xy -> Given frequency

N = ∑ f_x = ∑ f_y = 100

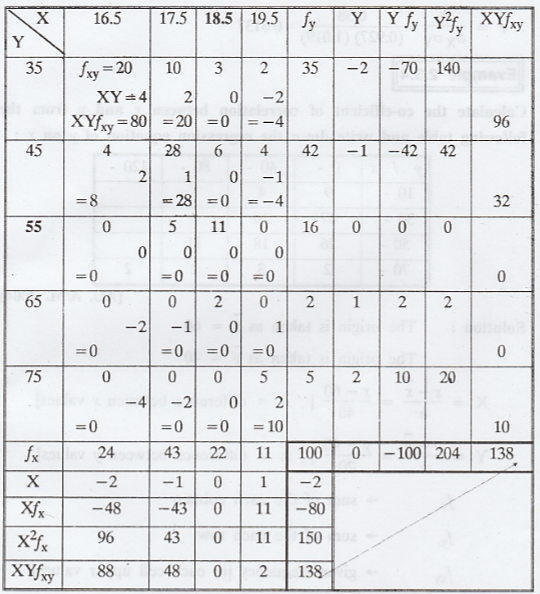
In each cell upper values are f_xy (given), middle are XY, lower are XYf_xy,

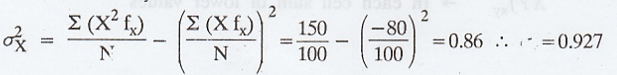
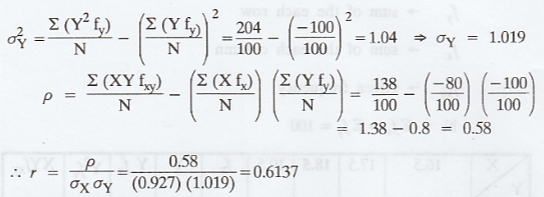
Example 2.3.4

Calculate the co-efficient of correlation between x and y from the following table and write down the regression equation of y on x :

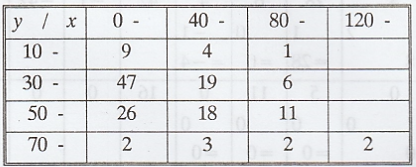[AU. A/M. 2004]

Solution :

The origin is taken as  = 60

The origin is taken as  = 40

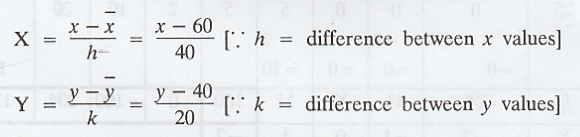
f_x -> sum of the each column

f_y -> sum of the each row

f_xy -> given frequency [in each cell upper values]

XY -> In each cell middle values

XYf_xy -> In each cell sum of lower values

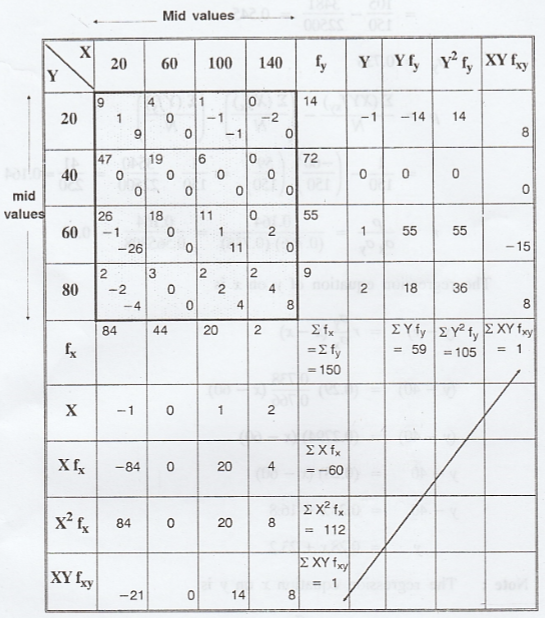
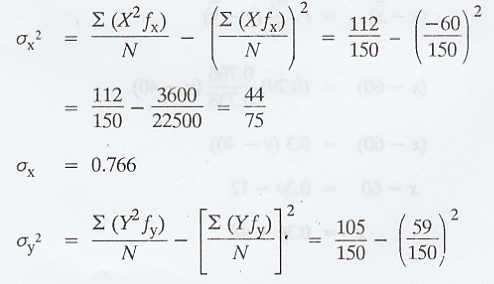
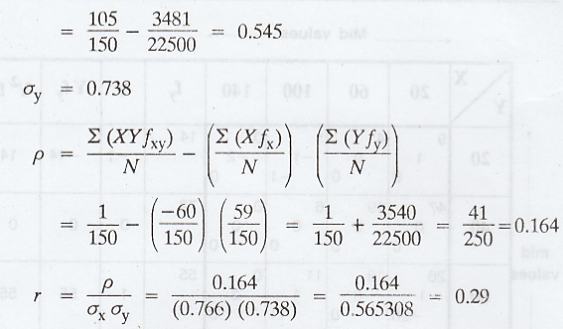
The regression equation of y on x is

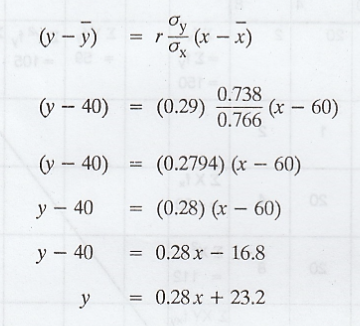
Note : The regression equation x on y is

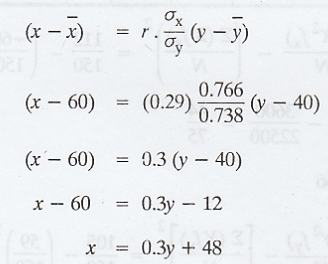
Example 2.3.5

For the following data find the most likely price at Madras corresponding to the price 70 at Bombay and that at Bombay corresponding to the price 68 at Madras.

S.D. of the difference between the price at Madras & Bombay is 3.1 ?[A.U. A/M. 2004] [A.U N/D 2017 R-08]

Solution:

Let X denote the price at Madras and Y denotes the price at Bombay.

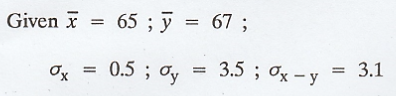
The correlation co-efficient r is given by

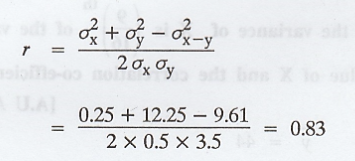
The line of regression of y on x is,

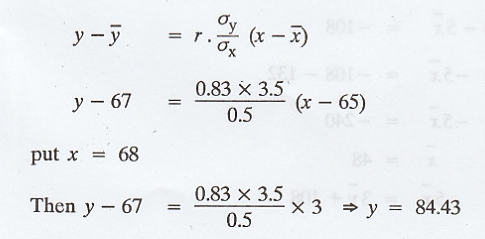
.'. Corresponding to the price 68 at Madras, the most likely price at Bombay is 84.43.

Similarly the line of regression of x on y is

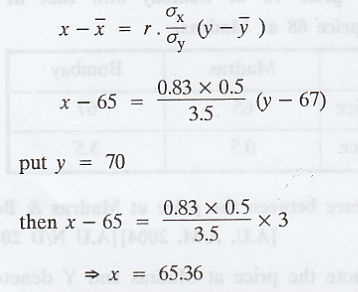
.'. Corresponding to the price 70 at Bombay, the most likely price at Madras is 65.36.

Example 2.3.6

The regression equation of X on Y is 3Y - 5X + 108 = 0. If the mean value of Y is 44 and the variance of X is (9/16)^th of the variance of Y. Find the mean value of X and the correlation co-efficient.

Solution:

 

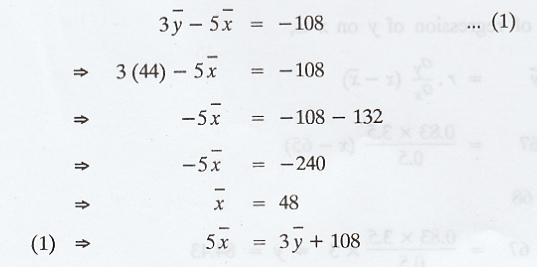
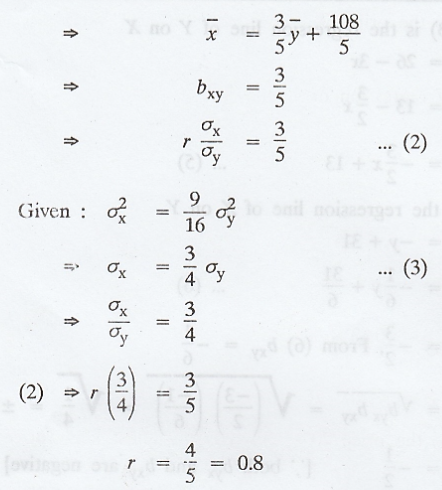
Example 2.3.7

The regression equations are 3x + 2y = 26 and 6x + y = 31. Find the correlation coefficient between X and Y. [A.U N/D 2011] [A.U N/D 2017 (RP) R-13] [A.U A/M 2019 (R17) PS]

Solution:

Given

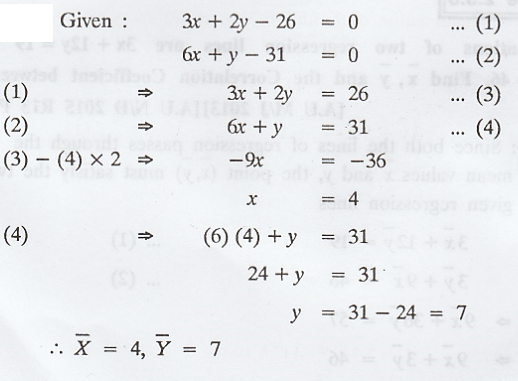
Assume that (3) is the regression line of Y on X

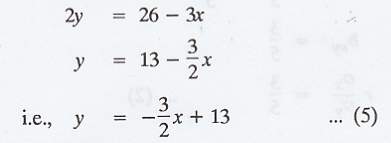
Assume that (4) is the regression line of X on Y

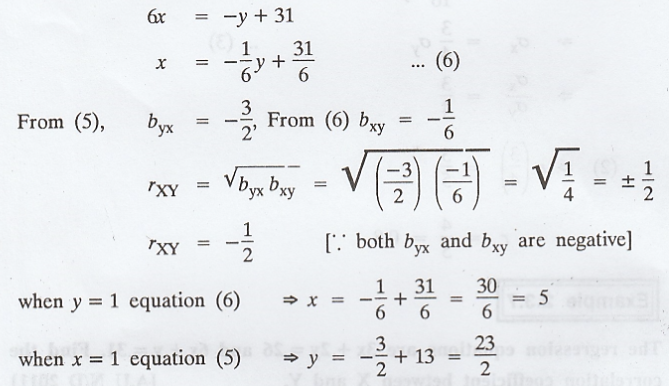
Example 2.3.8

The equations of two regression lines are 3x + 12y = 19 and 3y + 9x = 46. Find ,  and the Correlation Coefficient between X and Y. [A.U M/J 2013] [A.U N/D 2015 R13 PQT]

Solution:

Since both the lines of regression passes through the mean values , , the point must satisfy the two given regression lines

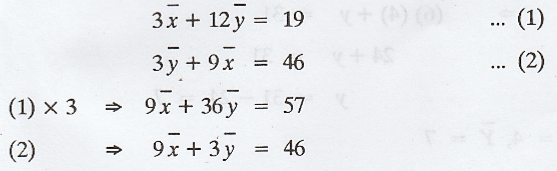
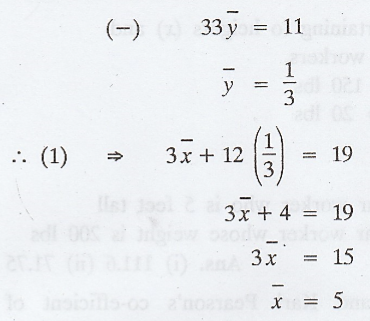
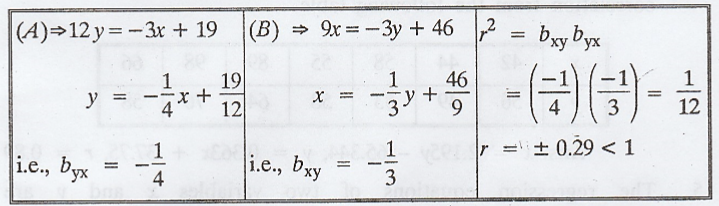
.'. r = -0.29 ['.' both the regression coefficients are negative]

EXERCISE 2.3

1. In a partially destroyed laboratory record, only the lines of regression of y on x and x on y are available as 4x - 5y + 33 = 0 and 20x - 9y = 107 respectively, calculate  and the coefficient of correlation between x and y.

Ans. r = ± 3/5

2. The following table gives the data on rainfall (x inches) and discharge in a certain river (y units). Obtain the line of regression- of y on x. Estimate from it, the discharge corresponding to a rainfall of 2 inches.

3. The following are results pertaining to heights (x) and weights (y) of 1000 industrial workers.

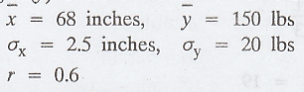
Estimate the following

(i) The weight of a particular worker who is 5 feet tall

(ii) The height of a particular worker whose weight is 200 lbs Ans. (i) 111.6 (ii) 71.75

4. Find the regression lines and Karl Pearson's co-efficient of correlation from the following table.

Ans. x = 2.195y  - 65.344, y = 0.363x + 37.75, r = 0.89

5. The regression equations of two and y are x = 0.7y+ 5.2 and y = 0.3x + 2.8. Find the means of the variables and the co-efficient of correlation between them. Ans. r = 0.458

6. The two regression lines are 3x + 2y = 26 and 6x + 3y = 31. Find the correlation co-efficient. Ans. r = -0.866

7. Given that 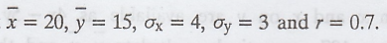 Find the two To in regression equations and find the value of y when x = 24. Ans. y = 17.1

8. The coefficient of correlation between two variables x and y is 0.8 and the regression co-efficient of y on x is 1.6. If  = 22,  = 20. Find the regression co-efficient of x on y and the two regression equations.

Ans. Regression equation of x on y: x = 0.4y + 14, Regression equation of y on x: y = 1.6x - 15.2

9. If the equations of the two lines of regression of y on x and x on y are respectively, 7x - 16y + 9= 0; 5y - 4x - 3 = 0, calculate the co-efficient of correlation,  and . [AU, May, '99]