Realization of Systems in Direct Form

Realization of Systems in Direct Form-ll

Direct form-II realization has the advantage that, it uses minimum number of integrators. Instead of using separate integrators for integrating the input and output variable separately, an intermediate variable is integrated. The following examples illustrate the procedures to obtain direct form-II realization of continuous-time system described by the transfer functions or differential equations.

Problem 4:

Realize an LTI system with the following transfer function in direct form - II

Solution:

Given:

Divide the given transfer function into two parts as follows:

Cross multiplying the above equations, we get

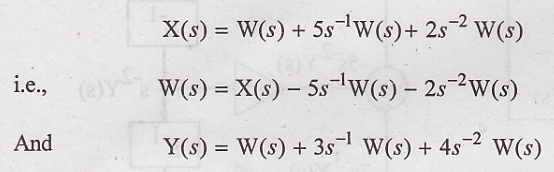
W(s) can be ralized as shown in figure 3.8(a) and Y(s) can be realized as shown in figure 3.7(b) cascading figures 3.8(a) and 3.8(b). We get the realization of H(s) as shown in figure 3.9 since the inputs and outputs of the integrators are the same, they can be treated as one as shown in figure 3.10.

Problem 5:

Realize the following system in direct form - II.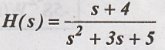 

Solution:

Given:

Transfer function is expressed in negative power of S as:

Dividing the transfer function into two parts we have

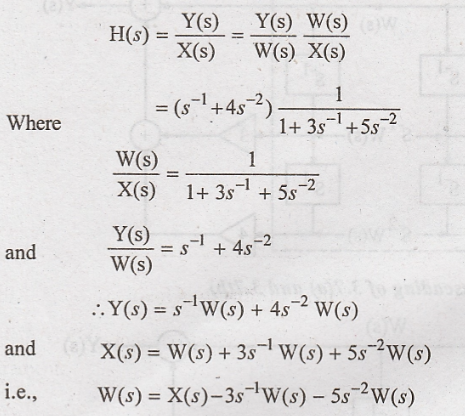
The given transfer function is realized in direct form-II as shown in figure 3.11.

Problem 6:

Realize the system described by the following differential equation in direct form-II: 

Solution:

The given differential equations is

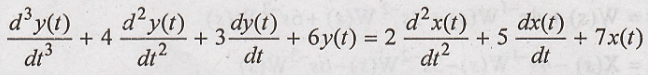
Taking Laplace transform on both sides and neglecting initial conditions, we have

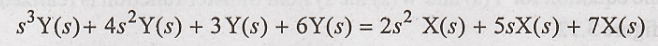
The transfer function of the system is

Using the equation for Y(s) and W(s) the system transfer function is realized as shown in the figure 3.12.

Realization of Systems in Cascade Form

In cascade form realization, the given transfer functions (of first and second order) and each of these transfer functions are realized in direct form II, and then all those realization structures are cascaded, I.e., connected in series, i.e., the output of the first one is connected to the input of the second one, the output of the second one to the input of the third and so on. The input is connected to the first one and the output is taken form the last one.

Problem 7:

Realize the system with transfer function H(s) =  in cascade form.

Solution:

The given transfer function is:

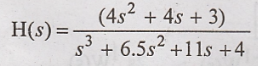
Expressing it as a product of several transfer function, we have

Each of these transfer functions can be realized in direct form-II as shown in figure.

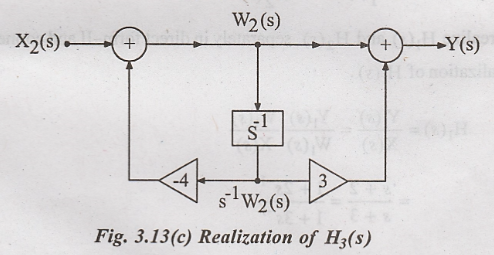
The individual realization of H₁(s), H₂(s) and H₃(s) are connected in cascade to get the cascade realization of the transfer function H(s) as shown in figure 3.14.

Problem 8:

Realize the system described by the following transfer function H(s) =  in cascade form.

Solution:

Given

In cascade form, H(s) = Y(s) / X(s)

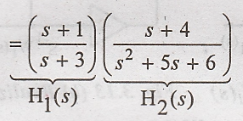
Now, realize H₁(s) and H₂(s) separately in direct form-II and connect them in cascade. Realization of H₁(s).

Let

Where,

The realization of H₁(s) is shown in figure 3.15(a)

Realization of H₂(s)

The realization of H₂(s) is shown in figure 3.15(b) is realized by cascading H₁(s) and H₂(s) as shown in figure. 3.16.

Realization of Systems in Parallel Form

In parallel form realization, the given transfer function is expressed into its partial fractions and each factor is realized structures are connected in parallel, i.e. The input is applied to each one of those structures and all the outputs are added together.

Problem 9:

Realize the system given by the following transfer function in parallel form:

H(s)=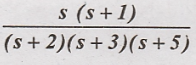 

Solution:

The given transfer function is;

In partial fraction form, it is:

Where the coefficients A, B, and C are:

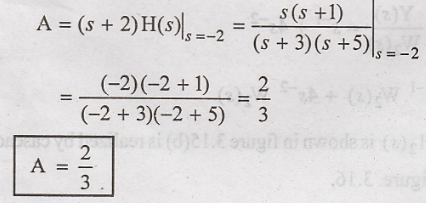
To realize H(s), realize H₁(s), H₂(s) and H₃(s) separately as shown in figure 3.17(a), 3.17(b), 3.17(c) and connect all of them in parallel as shown in figure 3.18.

Problem 10:

Realize the system with the following transfer function in parallel form:

H(s) = 

Solution:

The given transfer function is:

In partial fraction form, it is:

Now, to realize H(s) in parallel form, realize H₁(s) and H₂(s) separatery in direct form-II and connect them in parallel.

Realization of H1(s) in direct form - II

Based on the equations for W₁(s) and Y₁(s), H₁(s) is realized as shown in figure 3.19(a).

Realization of H₂(s) in direct form-II

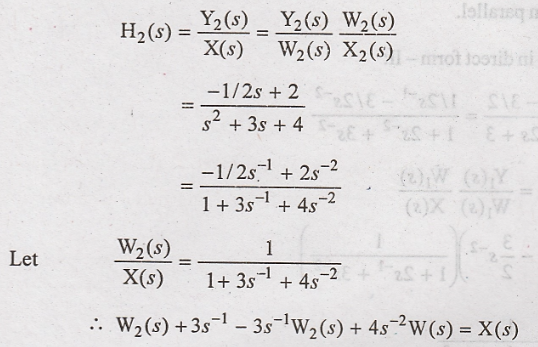
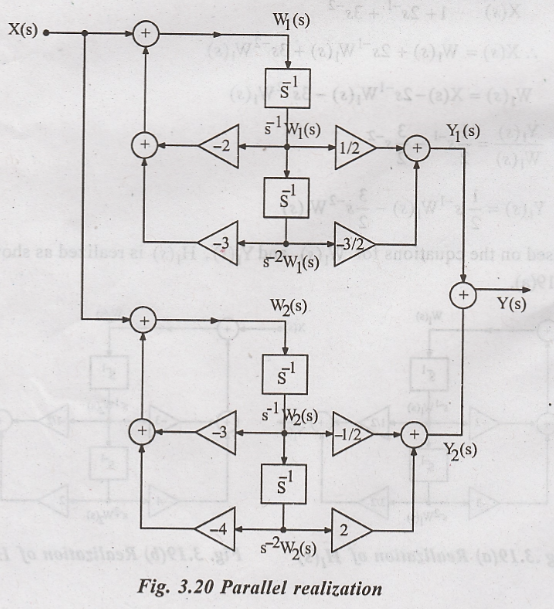
Based on these equations for W₂(s) and Y₂(s), H₂(s) is realized as shown in figure 3.19(b). Now H(s) is realized by connecting H₁(s) and H₂(s) in parallel as shown in figure 3.20.