Random Process and Linear Algebra: Unit I: Probability and Random Variables,,
Random Variable
A random variable is a rule that assigns a numerical value to each possible outcome of an experiment.
RANDOM VARIABLE
A random variable is a rule that assigns
a numerical value to each possible outcome of an experiment.
a. Discrete Random Variables, b.
Continuous Random Variables
i. Random variable [A.U
CBT Dec. 2009]
A real-valued function defined on the
outcome of a probability experiment is called a random variable.
ii. Probability distribution function of X.
If X is a random variable, then the
function F(x), defined by F(x) = P{X = x} is called the distribution function
of X.
(a) (i) Discrete random variable
A random variable whose set of possible
values is either finite or countably infinite is called discrete random
variable.
Example
1. Let X represent the sum of the
numbers on the 2 dice, when two dice are thrown. In this case the random
variable X takes the values 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12. So X is a
discrete random variable.
2. Number of transmitted bits received
in error.
(ii) Probability mass function
If X is a discrete random variable, then
the function P (x) = P[X=x] is called the probability mass function of X.
(iii) Probability distribution.
The values assumed by the random
variable X presented with corresponding probabilities is known as the
probability distribution of X.

(iv) Cumulative distribution or Distribution function floss of X
[for discrete R.V]
The cumulative distribution function
F(x) of a discrete random variable X with probability distribution P (x) is
given by
F(x) = P(X = x) = 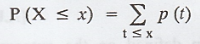
x = -∞,... -2, -1, 0, 1, 2, ... ∞.
(v) Properties of distribution function
1. F(-∞) = 0
2. F(∞) = 1
3. 0 ≤ F(x) ≤ 1
4. F(x1) ≤ F(x2)
if x1 < x2
5. P(x1 < X ≤ x2)
= F(x2) - F(x1)
6. P(x1 ≤ X ≤ x2)
= F(x2) - F(x1) + P[X = x1]
7. P(x1 < X < x2)
= F(x2) - F(x1) - P[X = x2]
8. P(x1 ≤ X < x2)
= F(x2) - F(x1) - P(X = x2) + P(X = x1)
(vi) Results.
1. P(X ≤ ∞) = 1
2. P(X ≤ -∞) = 0
3. If x1 ≤ x2 then
P (X = x1) ≤ P(X = x2)
4. P(X > x) = 1 - P[X ≤ x]
5. P(X ≤ x) = 1 - P(X > x)
(vii) Expected value of a Discrete random variable X
Let X be a discrete random variable
assuming values x1, x2, ..., xn with
corresponding probabilities p1, p2, ..., pn.
Then
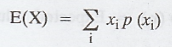
is called the Expected value of X.
E(X) is also called commonly the mean or
the expectation of X.
A useful identity states that for a
function g,
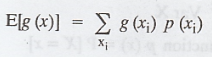
(viii) The variance of a random varaible X.
It is defined by Var(X) = E[X - E (X)]2
The variance, which is equal to the
expected value of the square of the difference between X and its expected
value. It is a measure of the spread of the possible values of X.
A useful identity is that
Var(X) = E[X2]-[E(X)]2
The quantity 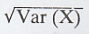 is called the
standard deviation of X.
is called the
standard deviation of X.
FORMULA

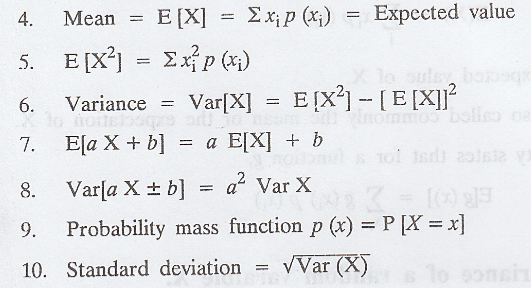
Note :
1. Prove that E[aX + b] = a E(X) + b.
Proof :
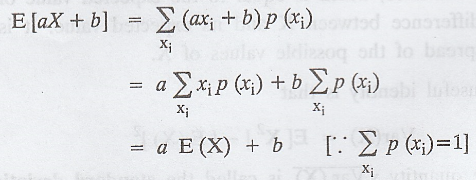
2. If X is a random variable then show
that
Var(ax + b) = a2 Var (X)
Proof :
Let Y = aX + b
E(Y) = E[aX + b]
We know that,

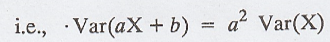
3. P[X = xi] = p(x)
-> Probability function (or)
Probability distribution (or) p.m.f (probability mass function)
4. f(x) -> p.d.f (probability density
function) (or) density function.
5. F(x) -> c.d.f (cumulative
distribution function) (or) distribution function.
Problems under the distribution function for discrete random
variable
Example 1.4.1
([Given P (xi) to find F (xi) type]
For the following probability
distribution (i) Find the distribution function of X. (ii) What is the smallest
value of x for which P(X ≤ x) > 0.5

Solution :
(i)

(ii) The smallest value of x for which P
(X ≤ xi) > 0.5 is 1.
Note : The smallest value of x for which
P (X ≤ xi) > 0.1 is 0 and
The smallest value of x for which P (X ≤ xi) > 0.8 is 2.
Example 1.4.2 [Given
F (xi) to find P (xi) type]
Obtain the probability function (or)
probability distribution from the following distribution function.

Solution :
To Find P(xi)

Example 1.4.3
The number of hardware failures of a
computer system in a week of operations has the following pmf:

Find the mean of the number of failures
in a week. [A.U. M/J 2006]
Solution :
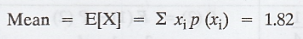

Example 1.4.4
Determine the mean, variance, E[(2X+1)],
Var(2X+1) of a discrete random variable X given its distribution as follows :

Solution :
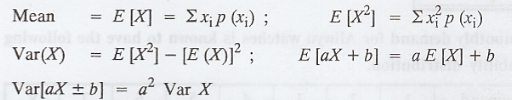

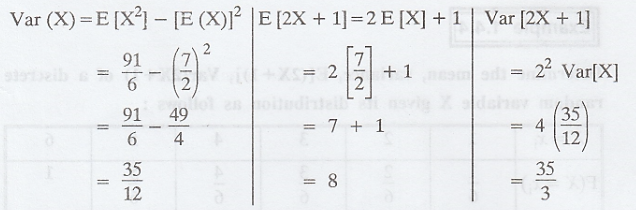
Example 1.4.5
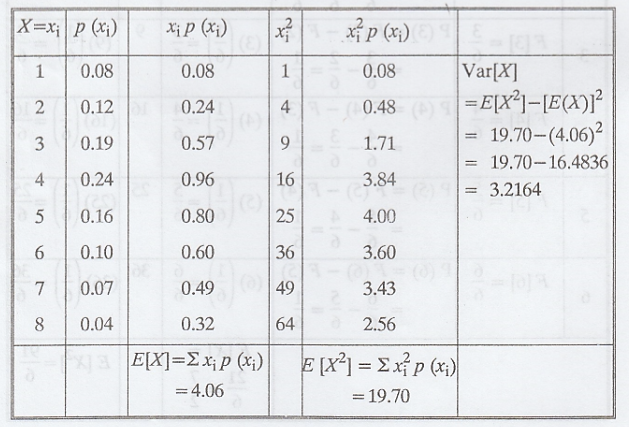
The monthly demand for Allwyn watches is
known to have the following probability distribution.

Determine the expected demand for
watches. Also compute the variance. [A.U. N/D 2006]
Solution:
Let X denote the demand
Example 1.4.6
When a die is thrown, X denotes the
number that turns up. Find E (X), E (X2) and var (X). [A.U. M/J
2006, A.U N/D 2019 (R17) PS]
Solution :
X is a discrete random variable taking
values, 1, 2, 3, 4, 5, 6 and with probability 1/6 for each

Example 1.4.7
Determine the constant K given the
following probability distribution of discrete random variable X. Also find mean
and Variance of X.

Solution:
We know that, 
we have, 0.1 + 0.2 + K + 2K + 0.1 = 1
i.e., 3K = 1 - 0.4 = 0.6
K = 0.2
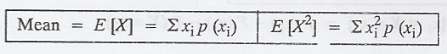
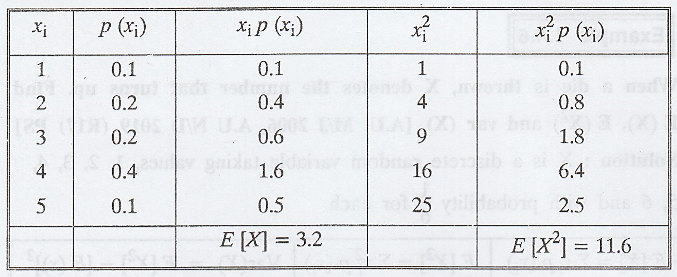
Var[X] = E[X2] - [E(X)]2
= 11.6 - (3.2)2 = 11.6 - 10.24 = 1.36
Example 1.4.8
If X has the distribution function
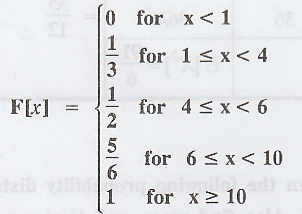
Find (1) The probability distribution of
X.
(2) P (2 < X < 6)
(3) Mean of X
(4) Variance of X. [A.U. A/M. 2008]
Solution:
(1) The probability distribution of X.
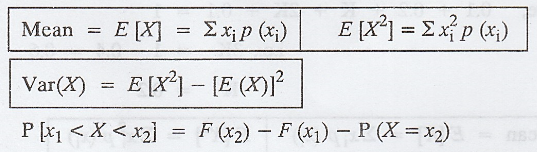


Formula:
(1) P(x1 < x < x2)
= F(x2) - F(x1) - P[X = x2]
(2) P(2 < X < 6) = F(6) - F(2) -
P(X = 6) = 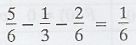
(3) Mean of X = E[X] = 28/6 = 14/3
(4) Variance of X = Var(X) = E[X2]
- [E[X]]2 =
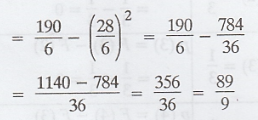
Example 1.4.9
A random variable X has the following
probability distribution.

Find
(1) The value of k,
(2) Evaluate P(X < 2) and P(-2 < X
< 2)
(3) Find the cumulative distribution of
X and
(4) Evaluate the mean of X. [A.U. N/D
2017 (RP) R-08] [A.U N/D 2018, R17 PS] [A.U. N/D 2007, M/J 2009, A.U CBT M/J 2010]
[A.U N/D 2011]
Solution:
(1) We know that,

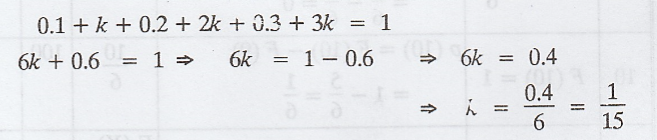
(2) (i) P[X < 2] = P[X = -2] + P[X
-1]+ P[X = 0] + P[X = 1]
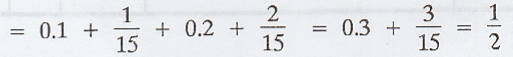
(ii) P [-2 < x < 2]
= P[X = -1] + P[X = 0] + P[X = 1]
=
1/15 + 0.2 + 2/15 = 0.2 + 3/15 = 2/5
(3)

(4) Mean = E[X] = 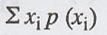 = 16/15
= 16/15
Example 1.4.10
A discrete random variable X has the
following probability distribution.

(i) Find the value of a. [A.U CBT N/D
2011, Trichy M/J 2011] [AU Tvli. A/M 2009]
(ii) Find P(X < 3), P(0 < x <
3), P(X ≥ 3)
(iii) Find the distribution function of
X.
Solution:
(i) We know that, 
a + 3a + 5a + 7a + 11a + 13a + 15a + 17a = 1
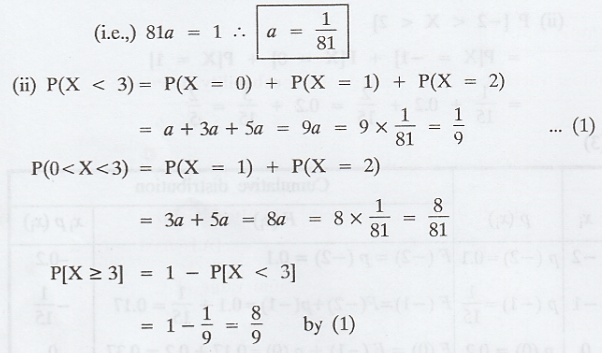
Distribution function F(x) of X.

Example 1.4.11
A random variable X has the following
probability function :

(a) Find K
(b) Evaluate P[X < 6], P[X ≥ 6]
(c) If P[X ≤ C] > 1/2, then find the
minimum value of C.
(d) Evaluate P [1.5 < X< 4.5/X
> 2]
(e) Find P [X < 2], P[X > 3], P[1
< X < 5] [A.U N/D 2010, M/J 2012, M//J 2014 [A.U A/M 2015 R-] [A.U M/J
2007, N/D 2008] [A.U. Tvli A/M 2009]
Solution:
(a) We know that, 
i.e., 0 + K + 2K + 2K + 3K + K2 + 2K2 +
7K2 + K = 1
i.e., 10 K2 + 9K - 1 = 0
=> K = -1 or K = 1/10
Since, P(X) ≥ 0 the value K = -1 is not
permissible
Hence, we have K = 1/10

(b) (i) P[X ≥ 6] = P [X = 6] + P[X = 7]
= 2/100 + 17/100 = 19/100
(ii) P [X < 6] = 1 - P[X ≥ 6]
= 1 - 19/100 = 81/100
(c)

The minimum value of C = 4. ['.' P[X ≤
C] > 1/2]
(d) P [1.5 < X < 4.5/X > 2]

(e)
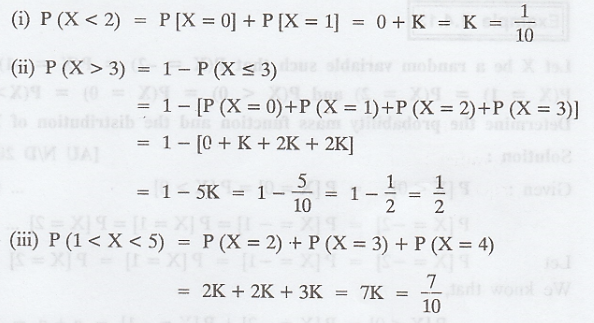
Example 1.4.12
A random variable 'X' has the following
probability function :

Find k, P [X ≥ 3] and P (0 < x <
4) [A.U. Tvli. A/M 2009]
Solution:
(i) We know that,
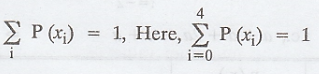
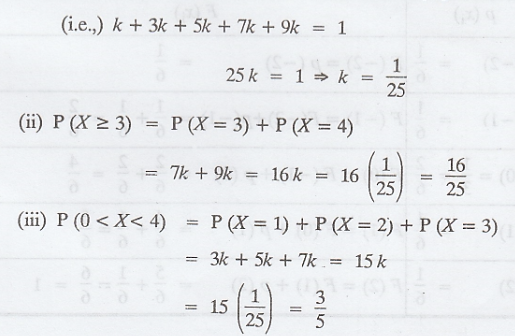
Example 1.4.13
Let X be a random variable such that P(X
= -2) = P(X = -1) = P(X = 1) = P(X = 2) and P(X < 0) = P(X = 0) = P(X >
0). Determine the probability mass function and the distribution of X. [AU N/D
2006]
Solution :
Given:
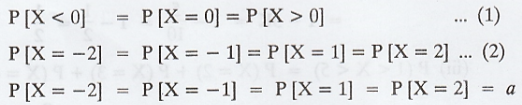
We know that,
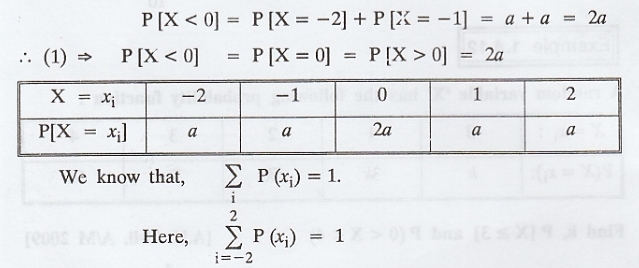
i.e., a + a + 2a + a + a = 1 => a = 1 => a = 1/6

Example 1.4.14
If the random variable X takes the
values 1, 2, 3 and 4 such that 2P(X = 1) = 3P(X = 2) = P(X = 3) = 5P(X = 4)
find the probability distribution and cumulative distribution function of X.
[A.U CBT A/M 2011, A.U N/D 2012, A.U A/M
2017 R8] [IIOS QM U.A [A.U A/M 2019 (R13) PQT] [A.U A/M 2015 (RP) R8]
Solution :
X is a discrete random variable.
Given: 2P[X = 1] = 3P[X = 2] = P[X = 3]
= 5P[X = 4]
Let 2P[X = 1] = 3P[X = 2] = P[X = 3] =
5P[X = 4] = k ...........(1)

We know that,
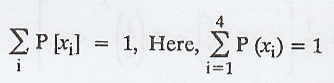
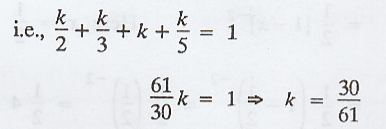

Example 1.4.15
The probability function of an infinite
discrete distribution is given by P[X = j] = 1/2j, j = 1, 2, ..., ∞.
Find the mean and variance of the distribution. Also find P[X is even], P [X ≥
5] and P[X is divisible by 3]. [A.U. N/D 2006] [A.U N/D 2011]
Solution: Given: P[X = j] = 1/2j
= (1/2)j
Mean = E[X] = 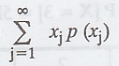
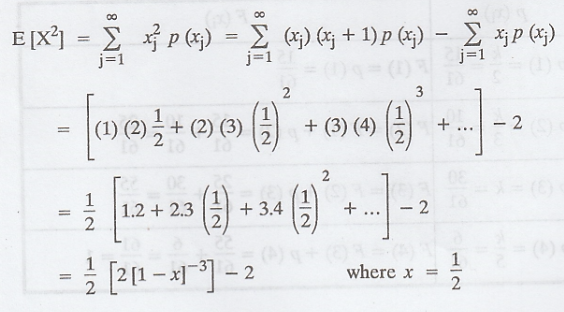
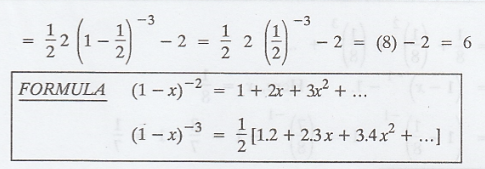
Variance of X = Var(X) = E[X2]
- [E[X]]2 = 6 - (2)2 = 6 - 4 = 2
(1) P[X is even] = P[X = 2] + P[X = 4] +
.....
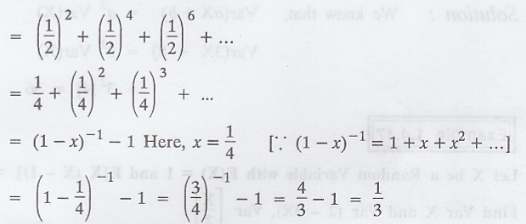
(2) P [X ≤ 5] = P[X = 5] + P [X = 6] +
...
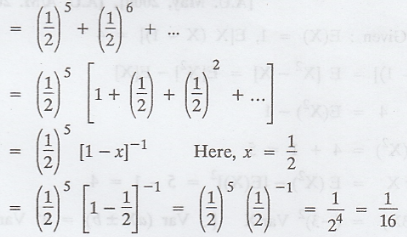
(3) P[X is divisible by 3] (or) P[X is
multiple of 3]
= P[X = 3] + P[X = 6] + ...
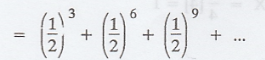
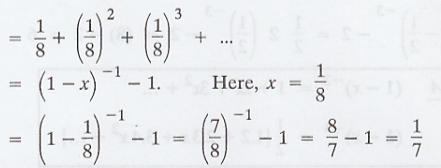
Example 1.4.16
If Var(X) = 4, then find Var(3X + 8),
where X is a random variable. [A.U, Model] [A.U Tvli M/J 2011]
Solution:
We know that, Var(aX + b) = a2
Var(X)
Var(3X + 8) = 32 Var(X) = 32[4]
= 36
Example 1.4.17
Let X be a Random Variable with E(X) = 1
and E[X (X - 1)] = 4. Find Var X and Var (2 - 3X), Var [X/2] [A.U. May, 2000],
[A.U. A/M. 2008]
Solution :

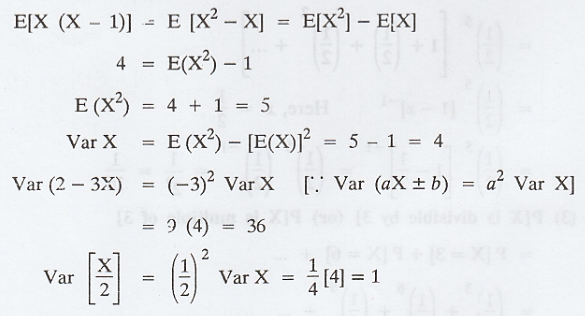
Example 1.4.18.
If the probability mass function of a
r.v. X is given by P(X = r) = kr3, r = 1, 2, 3, 4 find
(i) the value of k,
(ii) the mean and variance of X and
[A.U. A/M 2015 (RP) R13]
(iii) the distribution function of X
(iv) P (1/2 < X < 5/2 / X > 1)
[A.U Tvli. M/J 2010]
Solution :
(i) We know that, 
(ii) & (iii) Given: P(X = r) = kr3,
r = 1, 2, 3, 4

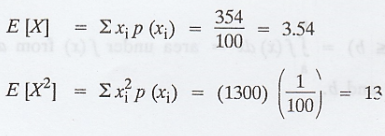
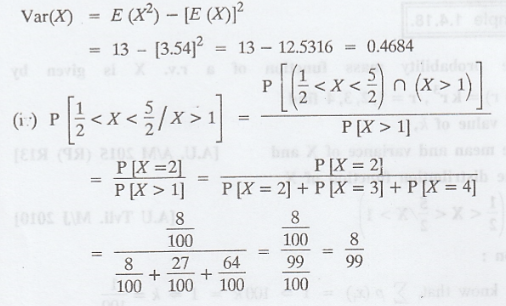
Random Process and Linear Algebra: Unit I: Probability and Random Variables,, : Tag: : - Random Variable
Related Topics
Related Subjects
Random Process and Linear Algebra
MA3355 - M3 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
