Projection

(d) Projection

Definition :

Let V be a vector space and W₁ and W₂ be subspaces of V such that 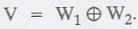 A function T: V → V is called the projection on W₁ along W₂ if, for x = x₁ + x₂ with x₁ Є W₁ and x₂ Є W₂, we have T(x) = x₁.

Problem 1.

Let T: R² → R²

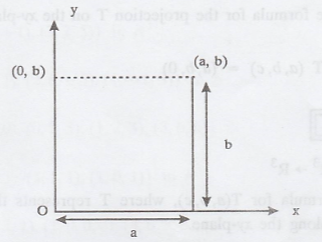
Find a formula for T(a, b), where T represent the projection on the y-axis along the x-axis.

Solution :

By definition, if T projects on the y-axis, then T(a, b) must results in the form (0, s).

Again, if it projects along the x-axis, the displacement vector.

T(a, b) ~ (a, b)

Must have the form (t, 0)

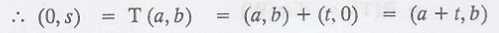
This gives the linear system has a solution,

t = -a, s = b

And therefore, T(a, b) = (0, b)

Problem 2.

Let T: R³ → R³

Find a formula for T(a, b, c) where T is the projection on the xy-plane along the z-axis.

Solution :

Let W₁ = xy-plane, W₂ = z-axis, and V = R³

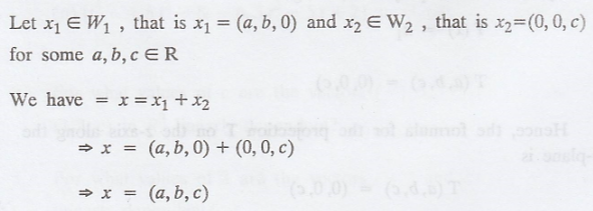
Using definition of projection, we get

T(x) = x₁

T(a, b, c) = (a, b, 0)

Hence, the formula for the projection T on the xy-plane along the z-axis.

T(a, b, c) = (a, b, 0)

Problem 3.

Let T: R³ → R³

Find a formula for T(a, b, c), where T represents the projection on the z-axis along the xy-plane.

Solution :

Let W₁ = z-axis, W₂ = xy-plane, and V = R³

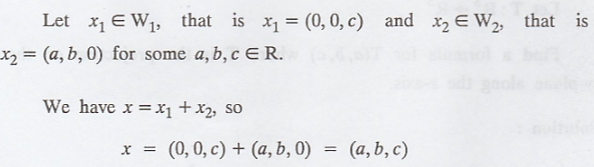
By definition of projection, we get

T(x) = x₁

T(a, b, c) = (0, 0, c)

Hence, the formula for the projection T on the z-axis along the xy-plane is

T(a, b, c) = (0, 0, c)

Problem 4.

T: V → V is the projection on W₁ along W₂.

Describe T if W₁ = V

Solution :

The objective is to describe T if W₁ = V.

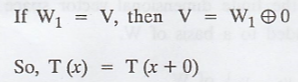
As T is the projection on W₁ along W₂, T(x) = X.

Hence, the required answer is T(x) = x, if x Є W₁

Problem 5.

T: V → V is the projection on W₁ along W₂. Describe T if W₁ is the zero subspace.

Solution :

The objective is to describe T if W₁ is the zero subspace.

If W₁ is the zero subspace, then W₁ = 0

So, T(x) = 0 for all x Є W₁

So, the required answer is T(x) = 0, for all x Є V if W₁ = 0

Problem 6.

Suppose that W is a subspace of a finite-dimensional vector space V.

Prove that there exists a subspace W' and a function T : V → V such that T is a projection on W along W'.

Solution :

Let W is a subspace of a finite-dimensional vector space V.

To prove that there exist a substance W' and a function that is projection on W along W'.

Suppose that {v₁, v₂, ..., v_k} is a basis for W.

Since W is a subspace of the finite dimensional vector space V, so the basis of W can be extended to a basis of W.

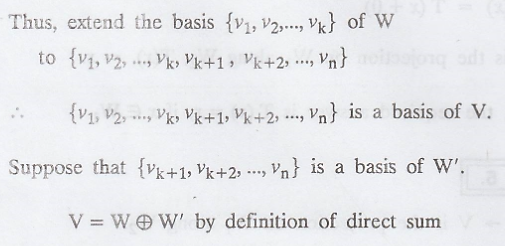
Hence, there exists a subspace W'.

Since, W is a subspace and there is a subspace W', so a projection T can defined from W to W'.

Problem 7

Suppose that W is a subspace of a finite-dimensional vector space V.

Give an example of a subspace W of a vector space V such that there are two projections on W along two (distinct) subspaces.

Solution :

The objective is to provide example of the subspace W such that there are two projections on W along two distinct subspaces.

Consider the vector space R².

Let T : R² → R² is defined as T(a, b) = (0, b)

Then T is a projection on y-axis along the x-axis.

Let L = {(s,s) : S Є R}

Define the function T as T(a, b) = (0, b - a)

Then T is a projection on y-axis along the line L.