Problems under n-step tpm pn

Type 4. n-step tpm pⁿ

Example 3.7.21

The transition probability matrix of the Markov Chain {X_n}, n = 1, 2, 3,... having 3 states 1, 2 and 3 is  and the initial distribution is P⁽⁰⁾ = (0.7 0.2 0.1) Find (i) P (X₂ = 3) and (ii) P [X₃ = 2, X₂ = 3, X₁ = 3, X₀ = 2] [A.U N/D 2006, A/M 2010, CBT M/J 2010, N/D 2011, Trichy M/J 2011] [A.U M/J 2013,N/D 2013] [A.U M/J 2012, A.U N/D 2015 R-8, N/D 2016 R-13, A/M 2017 R-8] [A.U A/M 2018 R-8] [A.U A/M 2019 R-13 PQT]

Solution :

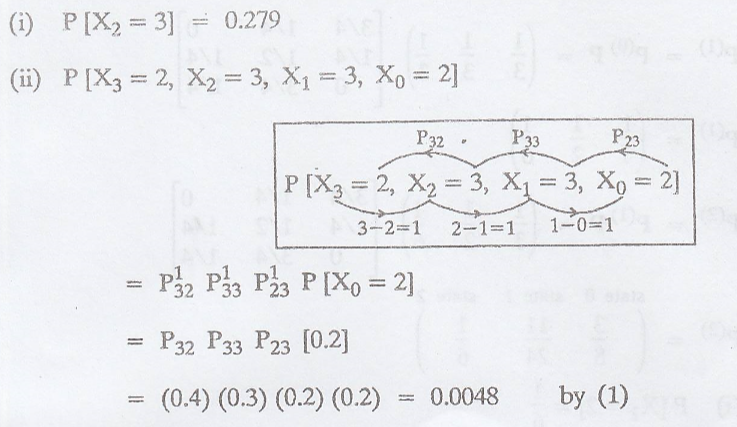
Example 3.7.22

The tpm of a Markov chain with three states 0, 1, 2 is 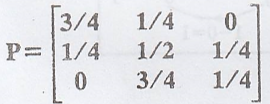 and the initial state distribution of the chain is P (X₀ = i) = 1/3, i = 0, 1, 2. Find (i) P (X₂ = 2) and (ii) P [X₃ = 1, X₂ = 2, X₁ = 1, X₀ = 2] [A.U A/M 2019 R-17 PQT]

Solution :

Given: P[X₀ = i] = 1/3, i = 0, 1, 2

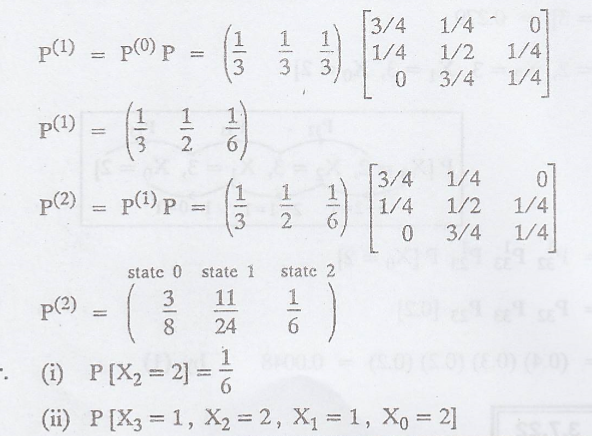
Example 3.7.23

The tpm of a Markov chain {X_n, n ≥ 0} have three states 0, 1 and 2.  and the initial distribution is P⁽⁰⁾= (0.5 0.3 0.2). Find (1) P[X₂ = 2], (2) P[X₃ = 1, X₂ = 2, X₁ = 1, X₀ = 2]

Solution:

Given: P⁽⁰⁾ = (0.5 0.3 0.2)

=> P[X₀ = 0] = 0.5, P[X₀ = 1] = 0.3, P[X₀ = 2] = 0.2

Classification of Markov Chain

(1) Irreducible chain

If 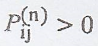 for some n and for every i and j then every state can be reached from every other state when this condition is satisfied, the Markov chain is said to be irreducible.

(OR)

If all states communicate with each other, then we say that the Markov chain is irreducible.

Note: A Markov Chain is irreducible if there is only one communicating class.

Example 1.

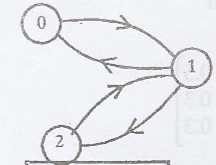
State 0 and state 1 are communicate with each other.

State 1 and state 2 are communicate with each other.

State 2 and state 0 are communicate each other through state 1.

.'. All the states are communicate with each other.

=> The Markov chain is irreducible.

Here the communicating class is {0, 1, 2}.

Example 2.

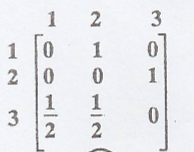
State 1 and state 2 are communicate with each other through state 3.

State 2 and state 3 are communicate with each other.

State 3 and state 1 are communicate with each other through state 2.

.'. All the states are communicate with each other.

=> The Markov chain is irreducible.

Here the communicating class is {1, 2, 3}.

Example 3.

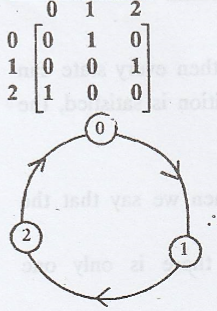
State 0 and state 1 are communicate with each other through state 2.

State 1 and state 2 are communicate with each other through state 0.

State 2 and state 1 are communicate with each other through state 1.

.'. All the states are communicate with each other

=> The Markov chain is irreducible.

Here the communicating class is {0, 1, 2}

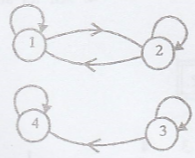
Example 4.

State 2 and state 3 are not communicate with each other.

=> The Markov chain is not irreducible.

The Markov chain has 3 classes {1, 2}, {3}, {4}.

Example 5.

State 0 and state 1 are not communicate with each other.

=> The Markov chain is not irreducible.

=> The chain has two classes {0}, {1}.

2. Periodic and Aperiodic states

The period d_i of a return state i is defined as the greatest common divisor of all m such that 

i.e., 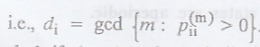. State i is said to be periodic with period di if di > 1 and aperiodic if d_i = 1.

Note : (1) Whenever 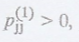, j is aperiodic.

(2) Any one state is aperiodic.

=> All its states are aperiodic.

Atleast One Diagonal element > 0

Example 1.

P₀₀ = 1 > 0 ⇒ State 0 is aperiodic

P₁₁ = 1/2 > 0 ⇒ State 1 is aperiodic

=> All its states are aperiodic.

Example 2.

P₄₄ = 1/4 > 0 => State 4 is aperiodic.

=> All its states are aperiodic.

Example 3.

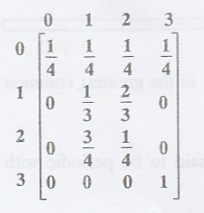
P₀₀ = 1/4 > 0, P₁₁ = 1/3 > 0,

P₂₂ = 1/4 > 0, P₃₃ = 1 > 0

=> All its states are aperiodic.

All the Diagonal elements = 0

Example 4.

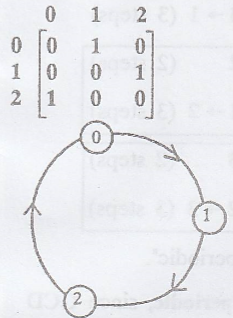
One can get back to

State 0 in 0→1→2→0 (3 steps)

State 1 in 1→2→0→1 (3 steps)

State 2 in 2→0→1→2 (3 steps)

=> All its states are not aperiodic.

['.' The states are periodic with period 3].

Example 5.

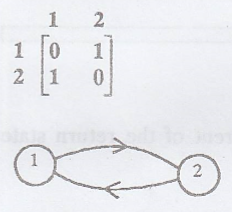
One can get back to

State 1 in 1→2→1 (2 steps)

State 2 in 2→1→2 (2 steps)

=> All its states are "not aperiodic".

['.' The states are periodic with period 2]

Example 6.

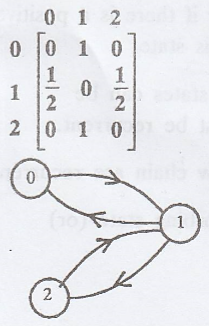
One can get back to

State 0 in 0→1→0 (2 steps)

State 1 in 1→0→1 (2 steps)

State 1 in 1→2→1 (2 steps)

State 2 in 2→1→2 (2 steps)

=> All its states are "not aperiodic"

['.' The states are periodic with period 2]

Example 7.

One can get back to

State 1 in 1→2→3→1 (3 steps)

State 2 in 2→3→2 (2 steps)

State 2 in 2→3→1→2 (3 steps)

State 3 in 3→2→3 (2 steps)

State 3 in 3→1→2→3 (3 steps)

=> All its states are "aperiodic".

['.' The states are not periodic, since GCD is not greater than 1]

3.(a) Recurrent or Persistent state

A state 'i' is said to be persistent or recurrent of the return state 'i' is certain, i.e., 

(b) Transient state

A state 'ï' is said to be transient if and only if there is a positive probability that the process will not return to this state.

Note 1: In a finite state Markov chain, not all states can be (transient. Atleast one of the states must be recurrent.

Note 2 : All states of a finite irreducible Markov chain are recurrent.

Note 3: P_ij = 1, for i = j then the state is Absorbing state (or) Trapping state.

Example 1.

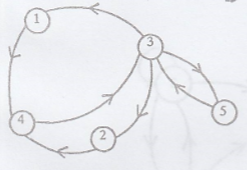
Here X_n = {1,2,3,4,5}

=> Finite ..............(1)

Here all the states are communicate with each other.

=> The Markov chain is irreducible. ... (2)

=> From (1) & (2) we get, All the states are recurrent.

Example 2.

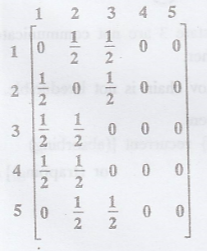
State 4 and state 2 are not communicate with each other.

.'. The Markov chain is not irreducible

{1, 2, 3} recurrent

{4} transient

{5} transient

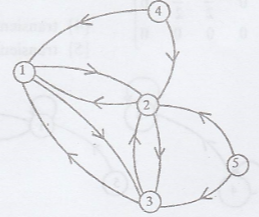
Example 3

State 3 and state 4 are not communicate with each other.

.'. The Markov chain is not irreducible.

{1, 2, 3} recurrent.

{4, 5} recurrent.

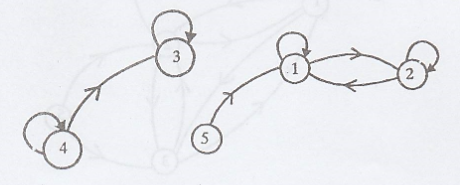
Example 4.

State 2 and state 3 are not communicate with each other.

.'. The Markov chain is not irreducible.

{1, 2} recurrent

P33 = 1 => {3} recurrent [(absorbing) or (trapping)]

{4} transient

{5} transient

 

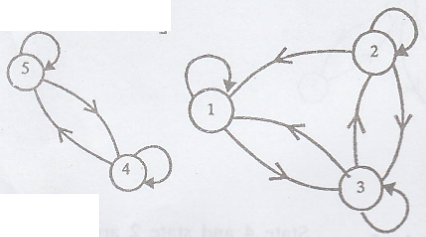
Example 5.

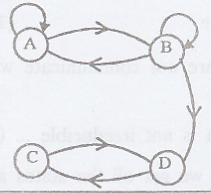
{A, B} transient

{C, D} recurrent.

4. Non-null persistent and Null persistent

The state 'i' is said to be non-null persistent if its mean recurrence time  is finite and null persistent if µ_ii = ∞

Note: If a Markov chain is finite and irreducible then all its states are non-null persistent.

Example 1.

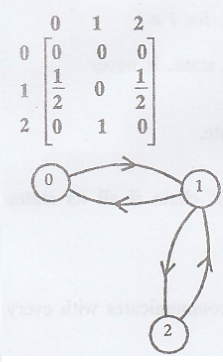
X_n = {0, 1, 2} => finite ..........(1)

State 0 and state 1 are communicate with each other.

State 1 and state 2 are communicate with each other.

State 2 and state 0 are communicate with each other.

All the states are communicate with each other.

=> The Markov chain is irreducible. ..........(2)

From (1) & (2) we get all the states are persistent and non-null.

Example 2.

X_n = {0, 1} => finite .......... (1)

State 0 and state 1 are not communicate with each other.

=> The Markov chain is not irreducible ..........(2)

=> From (1) and (2) we get all the states are not persistent and non-null.

5. Ergodic state

A non-null persistent and aperiodic state is called Ergodic.

6. Absorbing state (or) Trapping state

A state of a Markov chain is called an absorbing state if no other state is accessible from it.

i.e., P_ij = 1, for i = j; P_ij = 0, for i≠j

Note 1. Once the process enters a absorbing state, it never leaves the state.

Note 2. An absorbing state is a recurrent state.

7. Ergodic chain

A Markov chain is said to be an Ergodic chain if all its states are Ergodic.

8. Essential state

A state i' is called an essential state if it communicates with every state.

i.e., Assume  is an essential state.

Example [A.U M/J 2004]

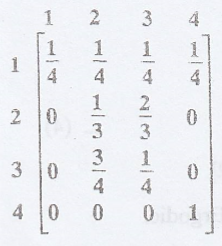
State 2 and state 3 are communicate with each other. So they are essential states.

State 1 leads to all states but not lead by other states. So state 1 is not an essential state.

TYPE 5.

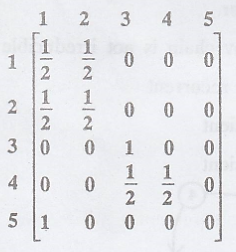
Example 3.7.23

Find the nature of the states of the Markov chain with the tpm.

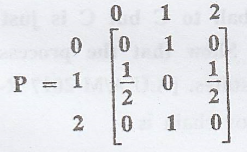 [A.U N/D 2019 R-17 PQT, RP] 0 [A.U. N/D 2004, N/D 2014, M/J 2013]

[A.U N/D 2016 R-13, A.U A/M 2018 R-13]

Solution :

(a) Given: X_n = {0, 1, 2} finite ................(1)

(b)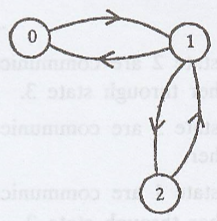 

State 0 and state 1 are communicate with each other.

State 1 and state 2 are communicate with each other.

State 2 and state 0 are communicate with each other through state 1.

=> The Markov chain is irreducible ..........(2)

(c) From (1) & (2) we get all its states are non-null-persistent ..........(3)

(d) One can get back to

State 0 in 0→1→0 (2 steps)

State 1 in 1→0→1 (2 steps)

State 1 in 1→2→1 (2 steps)

State 2 in 2→1→2 (2 steps)

=> The state are not aperiodic .............(4)

['.' The states are periodic with period 2]

(e) From (3) and (4) we get the states are not Ergodic.

Example 3.7.24

Prove that the matrix  1 is the tpm of an irreducible Markov chain. [A.U. M/J 2009] [A.U. N/D 20071

[OR]

Three boys A, B, C are throwing a ball each other. A always throws the ball to B and B always throws the ball to C but C is just as likely to throw the ball to B as to A. Show that the process is Markovian. Find the tpm and classify the states. [A.U A/M 2017 R-13]

Solution:

The tpm of the given Markov chain is

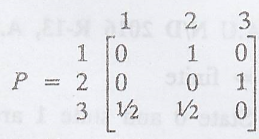
(a) Let X_n ={1, 2, 3} => finite ...........(1)

(b)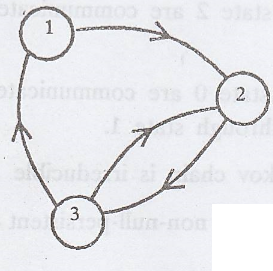 

State 1 and state 2 are communicate with each other through state 3.

State 2 and state 3 are communicate with each other.

State 3 and state 1 are communicate with each other through state 2.

=> The Makov chain is irreducible .............(2)

(c) From (1) and (2) all the states are persistent and non-null. .......(3)

(d) One can get back to

State 1 in 1→2→3→1 (3 steps)

State 2 in 2→3→2 (2 steps)

State 2 in 2→3→1→2 (3 steps)

State 3 in 3→1→2→3 (3 steps)

State 3 in 3→2→3 (2 steps)

=> The states are aperiodic ............(4)

['.' The states are not periodic]

(e) From (3) and (4) we get all the states are Ergodic.

Example 3.7.25

Consider the Markov chain with tpm given by

 Show that it is Ergodic.

Solution :

(a) Let X_n = {1, 2, 3, 4} finite .................(1)

(b)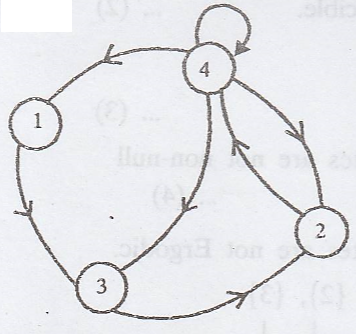 

State 1 and State 2 are communicate with each other through state '3' & '4'.

State 2 and State 3 are communicate with each other through state '4'

State 3 and State 4 are communicate with each other through state '2'

State 4 and State 1 are communicate with each other through state '3' & '2'.

.'. All the states are communicate with each other.

=> The Markov chain is irreducible. ................(2)

(c) From (1) and (2) we get all its states are non-null persistent. ...........(3)

(d) Here P₄₄ = 1/4 > 0 => The states are aperiodic. .............(4)

(e) From (3) & (4) we get all the states are Ergodic.

Example 3.7.26

Consider the Markov chain with tpm

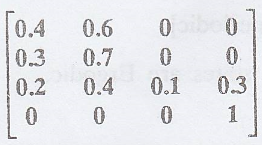
Is it irreducible? If not find the classes. Find the nature of the state.

Solution :

(a) Let X_n = {0, 1, 2, 3} => finite ............(1)

(b) 

State 3 and state 1 are not communicate with each other.

=> The Markov chain is not irreducible. ................(2)

(c) Here P₃₃ = 1 > 0

=> All the states are aperiodic. ..................(3)

(d) From (1) and (2) we get all the states are not non-null persistent. ..............(4)

(e) From (3) and (4) we get all the states are not Ergodic.

(f) The classes of the chain are {0, 1}, {2}, {3}.

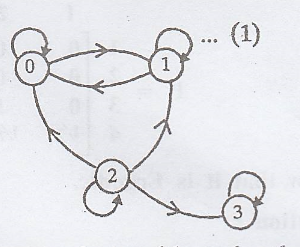
Example 3.7.27

Consider a Markov chain with state space {0, 1} and the tpm

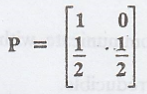
(i)Draw a transition diagram.

(ii) Show that state 0 is recurrent.

(iii) Show that state 1 is transient.

(iv) Is the state 1 periodic? If so, what is the period?

(v) Is the chain irreducible?

(vi) Is the chain Ergodic? Explain. [A.U. A/M. 2007]

Solution :

Let X_n = {0, 1} => finite

Given: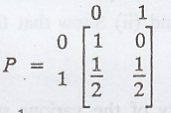 

(ii) Here, P₀₀ = 1

=> State 0 is recurrent.

['.' All absorbing states are recurrent]

(iii) State 1 is transient.

[.'. A state i is said to be transient if and only if there is a positive probability that the process will not return to this state]

(iv) In state 1, P₁₁ = 1/2 > 0

=> State 1 is aperiodic. ...............(2)

(v) State 0 and State 1 are not communicate with each other.

=> The Markov chain is not irreducible. ................(3)

(vi) The Markov chain is not irreducible.

The states are not non-null persistent.

=> Hence the chain is not Ergodic.

EXERCISE 3.7

1. Consider a Markov chain on the non-negative integer such that starting from x, the chain goes to state x + 1 with probabilities p, 0 < p < 1 and goes to state 0 with probabilities (1 − p), (i) show that the chain is irreducible, and (ii) Show that the chain is recurrent.

2. Determine the class and the periodicity of the various states for a Markovian chain with tpm  and show that the chain is irreducible.

3. For the Markov Chain with transition matrix P = 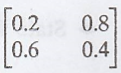 P(0) = (0.7 0.3). Find P(1), P(4) and P(8).

4. Does the transition matrix  Correspond to an absorbing Markov Chain?