Problems Under Continuous Random Variables

PROBLEMS UNDER CONTINUOUS RANDOM VARIABLES

Example 2.1.9

Suppose the point Probability Density Function (PDF) is given by

f(x, y) =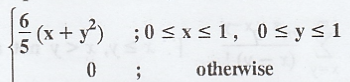 

Obtain the marginal PDF of X and that of Y. Hence, otherwise find 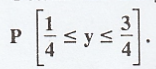 [A.U. N/D 2004, N/D 2005, N/D 2012] [A.U A/M 2019 (R-8) RP]

Solution:

Given that f(x, y) =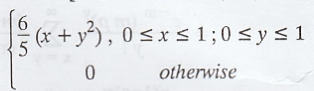 

The marginal p.d.f of X is,

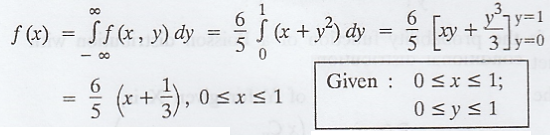
The marginal p.d.f of Y is,

Example 2.1.10

Let X and Y have j.p.d. f(x, y) = 2, 0 < x < y < 1. Find the m.d.f. find the conditional density function of Y given X=x. [A.U. A/M 2003] [A.U CBT A/M 2011]

Solution:

The marginal density function of X is given by

Here y varies from y = x to y = 1 [Vertical strip]

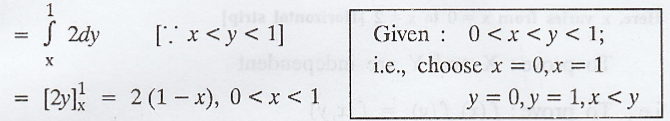
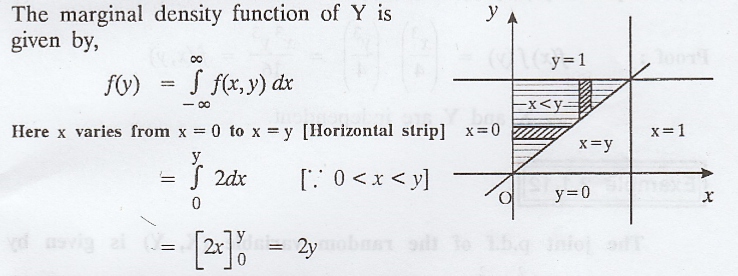
The conditional density function of Y given X = x is,

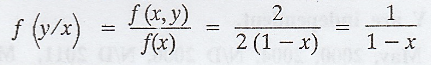
Example 2.1.11

The joint probability density function of a random variable X and Y is given by, 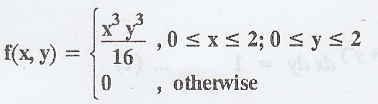 Find the marginal densities of X and Y. Also, prove that X and Y are independent.

Solution :

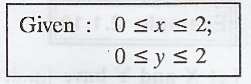
The marginal density of X is given by, 

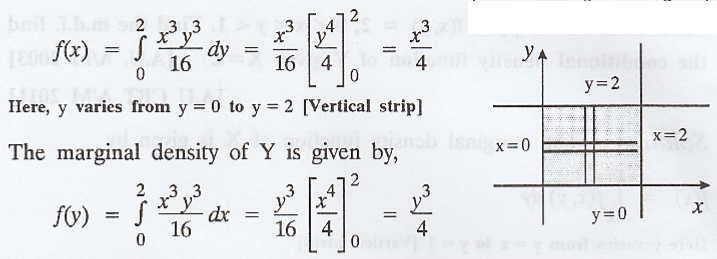
Here, x varies from x = 0 to x = 2 [Horizontal strip]

To prove X and Y are independent

i.e., To prove : f(x) f(y) = f(x, y)

Proof :

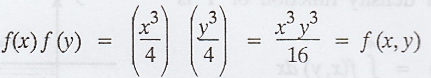
.'. X and Y are independent.

Example 2.1.12

The joint p.d.f of the random variable (X, Y) is given by 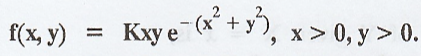. Find the value of K and also prove that X and Y are independent. [A.U. May, 2000, 2004, N/D 2006, N/D 2011, M/J 2012] [N/D 2007, M/J 2009, Tvli A/M 2009, N/D 2013] [A.U A/M 2015 (RP) R13, R8] [A.U N/D 2018 R-13 RP]

Solution:

Here, the range space is the entire first quadrant of the xy-plane.

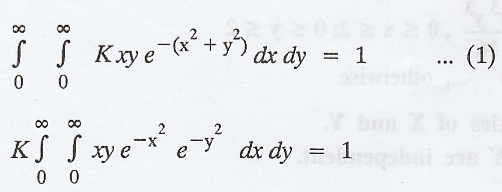
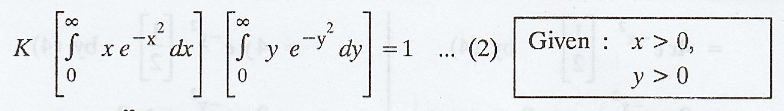
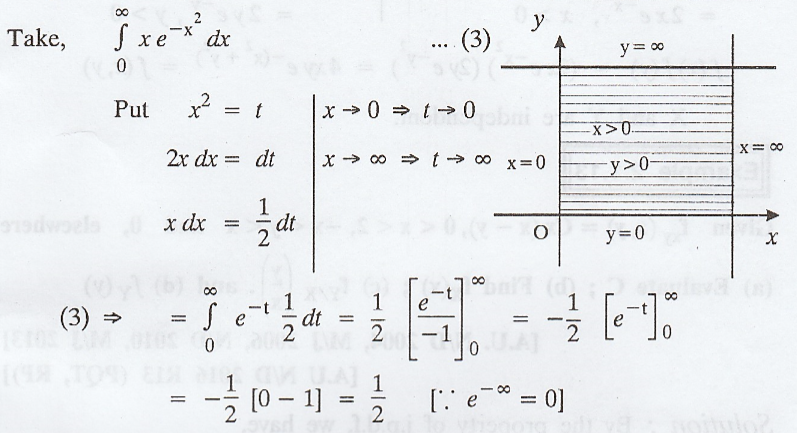
To prove : X and Y are independent

i.e., To prove : f(x) f(y) = f (x, y)

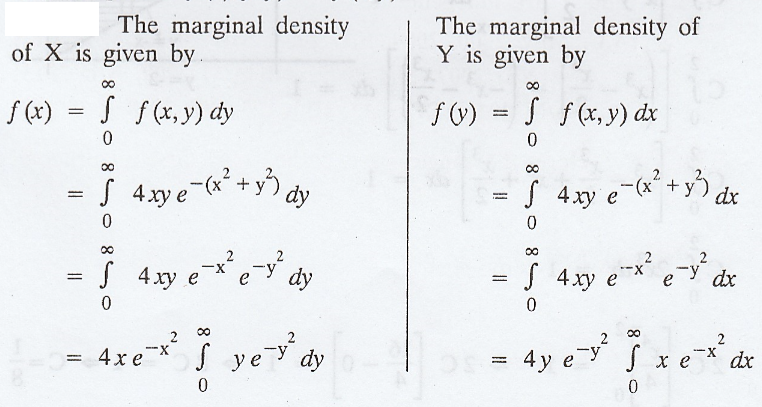
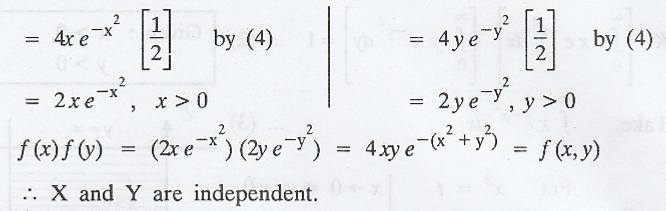
Example 2.1.13

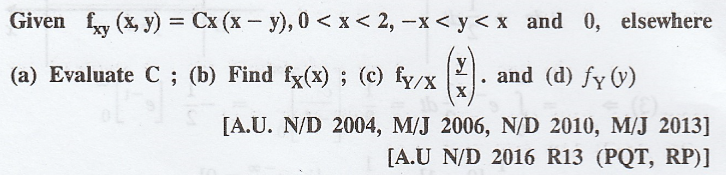
Solution :

By the property of j.p.d.f, we have,

(b) The marginal density of X is given by,

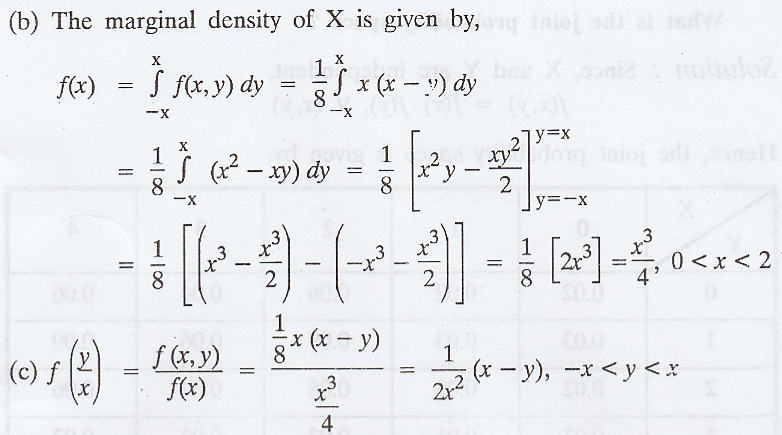
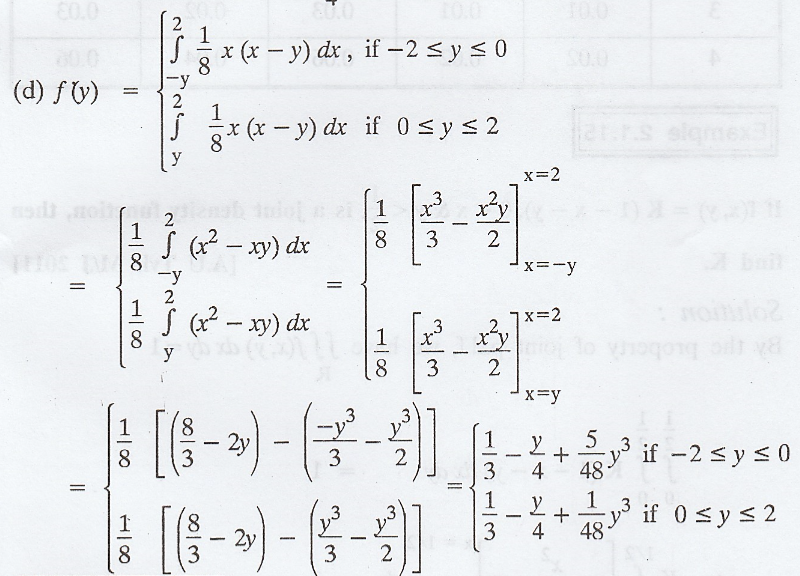
Example 2.1.14

Suppose that X and Y are independent and that these are the distribution tables for X and Y.

What is the joint probability space?

Solution

Since, X and Y are independent,

f(x, y) = f(x).f(v), V (x, y)

Hence, the joint probability space is given by,

Example 2.1.15

If f(x, y) = K (1 - x - y), 0 < x & y < 1/2, is a joint density function, then find K. [A.U Tvli M/J 2011]

Solution :

By the property of joint p.d.f, we have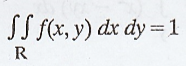 

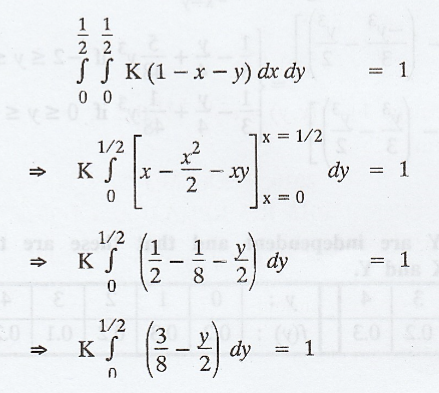
Example 2.1.16

If the joint p.d.f of (X, Y) is f(x, y) = 6e^-2x-3y, x = 0, y = 0, find the marginal density of X and conditional density of Y given X.

Solution:

The marginal density of X is given by

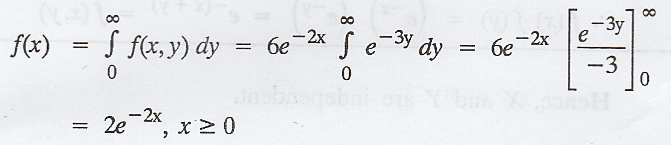
The conditional density of Y given X = x is

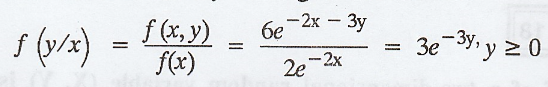
Example 2.1.17

The j.p.d.f of (X, Y) is given by f(x, y) = e^{-(x + y)}, 0 ≤ x, y < ∞. Are X and Y independent? Why? [A.U. A/M.2008] [A.U Tvli M/J 2010, Trichy M/J 2011, N/D 2011] [A.U N/D 2015 R13 RP] [A.U A/M 2017 R-13]

Solution:

Given: f (x, y) = e^{-(x + y)}, 0 ≤ x, y < ∞

To prove : X and Y are independent.

i.e., To Prove: f(x)f (v) = f(x, y)

Hence, X and Y are independent.

Example 2.1.18

If the joint pdf of a two-dimensional random variable (X, Y) is given by, 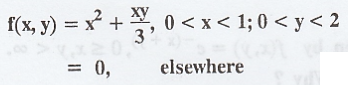 Find (i) P X > 1/2 ; (ii) P (Y < X) and (iii) P (Y < 1/2 / X < 1/2) Check whether the conditional density functions are valid. [A.U. M/J 2006] [A.U. N/D 2006] [A.U Trichy A/M 2010] [A.U A/M 2011, M/J 2009, M/J 2014] [A.U A/M 2015 (RP) R8] [A.U N/D 2019 (R-17) PS]

Solution :

Given 0 < x < 1, 0 < y < 2

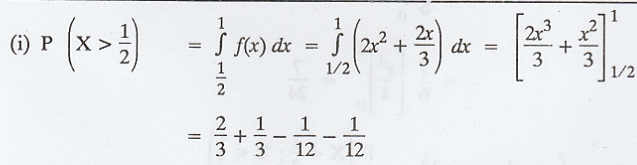
(ii) To find P[Y < X]

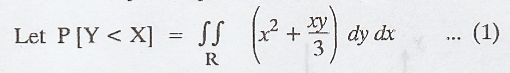
Here, outer limit x is 0 < x < 1

i.e., x limit varies from x = 0 to x = 1;

inner limit y. Here, Y < X, 0 < y < 2

Checking the conditional density functions are valid

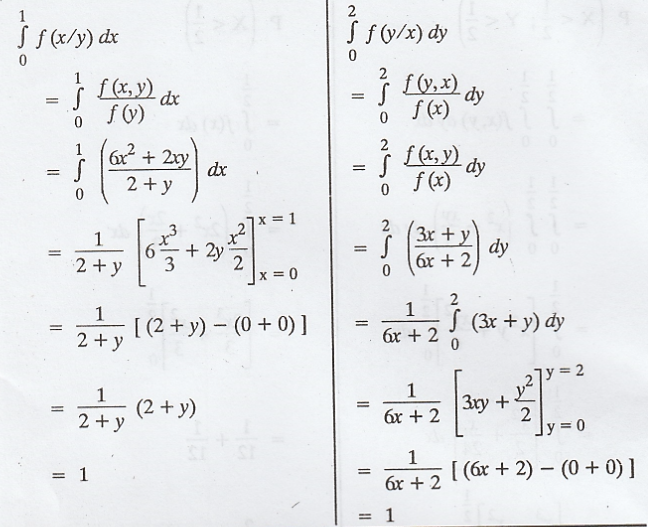
Example 2.1.13

Given that the joint p.d.f of (X, Y) is  Find (i) P (X > 1/ Y < 5) and (ii) the marginal distributions of X and Y

Solution:

Given: x > 0, y > x

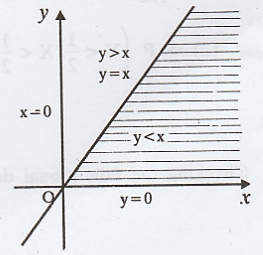
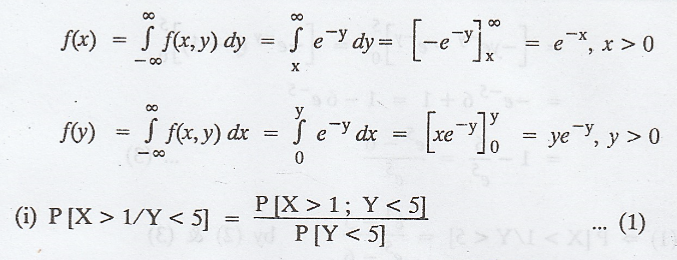
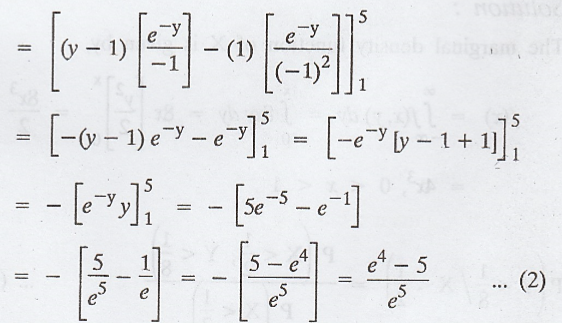
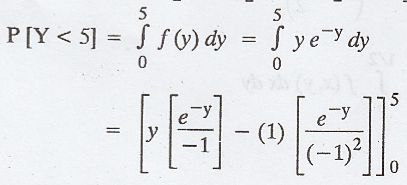
Example 2.1.20

The joint density function of the RVs X and Y is given by,

f(x, y) = 8xy, 0 < x < 1 ; 0 < y < x

= 0, elsewhere

Find P (Y < 1/8 / X < 1/2). Also find the conditional density function of f(y/x) [A.U Trichy A/M 2010] [AU, May 1999, N/D 2005, N/D 2009]

Solution:

The marginal density function of X is given by,

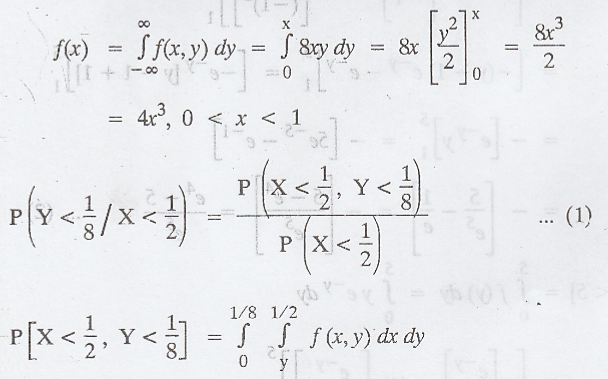
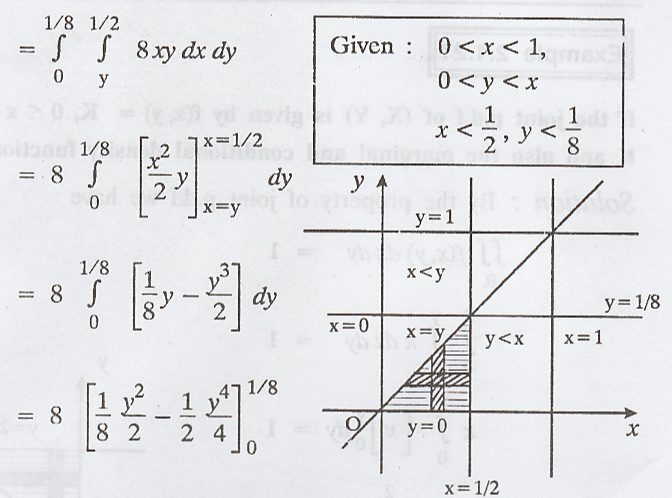
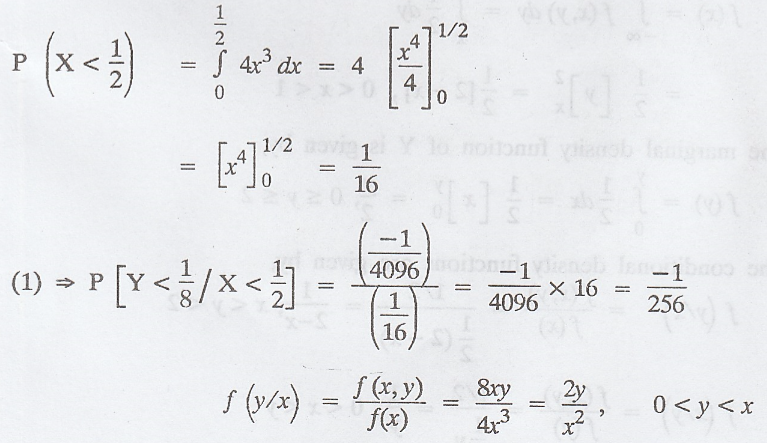
Example 2.1.21

If the joint p.d.f of (X, Y) is given by f(x, y) = K, 0 ≤ x < y ≤ 2 find K and also the marginal and conditional density functions.

Solution

By the property of joint p.d.f we have

The marginal density function of X is given by,

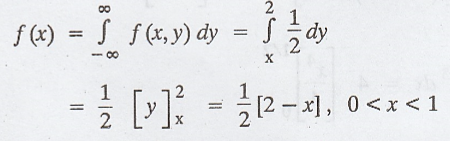
The marginal density function of Y is given by,

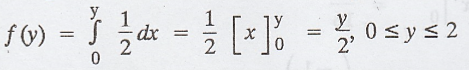
The conditional density functions are given by,

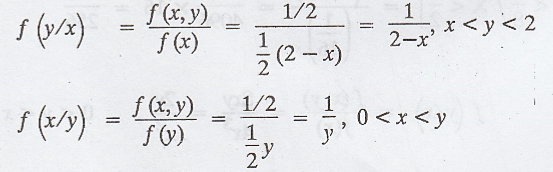
Example 2.1.22

If the joint density function of the two random variables 'X' and 'Y' be 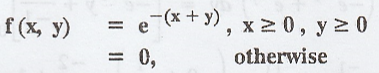 Find (i) P(X < 1) and (ii) P(X + Y < 1) [A.U N/D. 2003] [A.U N/D. 2009] [A.U CBT M/J 2010] [A.U N/D 2019 (R17) PQT]

Solution :

To find the marginal density function of X.

Let the marginal density function of X be g(x) and it is defined as

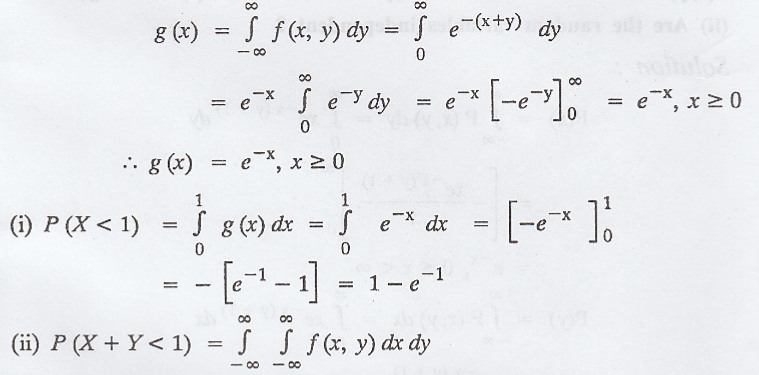
'x' varies from '0' to (1 - y) and 'y' varies from '0' to '1'.

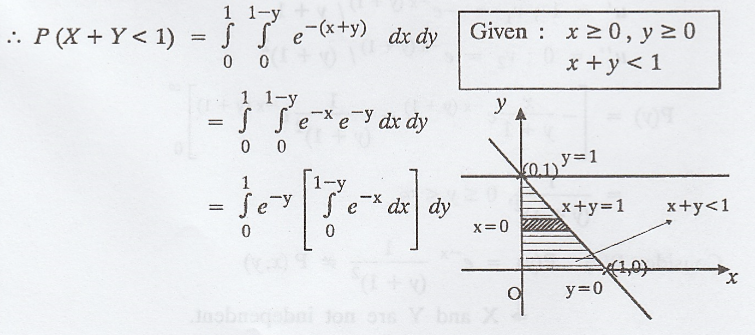
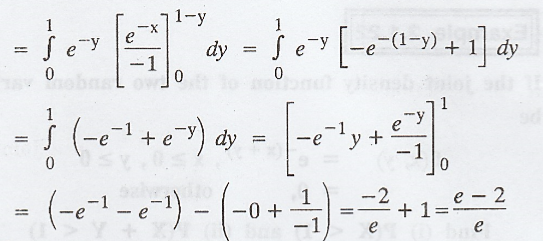
Example 2.1.23

The joint p.d.f of the random variables X and Y is given by P(x, y) = xe^-x(y+1) where 0 ≤ x, y < ∞. (i) Find P(x) and P(y) and (ii) Are the random variables independent ?

Solution :

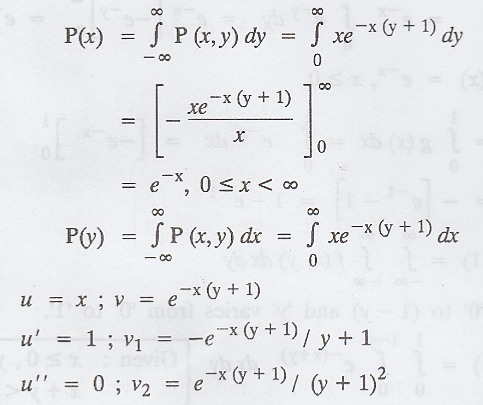
=> X and Y are not independent.

Example 2.1.24

S.T. the function 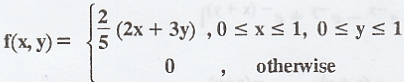 is a joint p.d.f of X and Y [AU N/D 2006] [A.U N/D 2018 R-13 RP]

Solution :

Example 2.1.25

If the joint distribution function of X and Y is given by

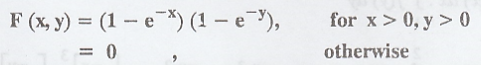
(i) Find the marginal density of X and Y

(ii) Are X and Y independent ?

(iii) P(1 < x < 3, 1 < Y < 2) [AU N/D 2008] [A.U A/M 2015 (RP) R13] [A.U N/D 2019 (R17) PS]

Solution :

Given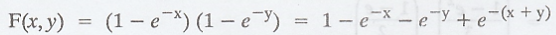  

The joint p.d.f is given by, f(x, y) =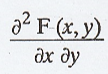 

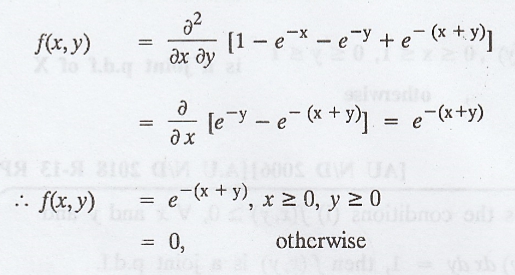
(i) The marginal density function of X is f(x) =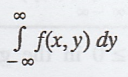 

Similarly the marginal density function of Y is f(y) =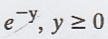 

(ii) Consider f(x).f(y) =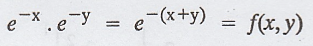 

=> X and Y are independent.

(iii) P (1 < X < 3, 1 < Y < 2) P(1 < X < 3) P(1 < Y < 2)

['.' X and Y are independent]

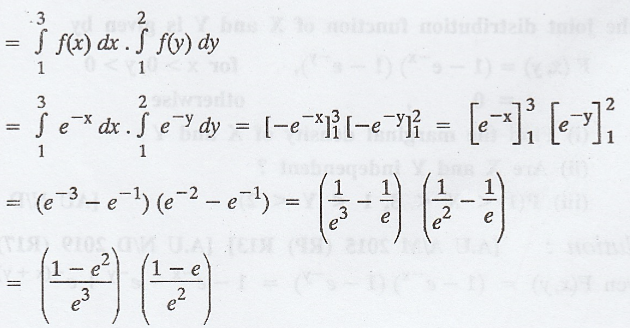
Example 2.1.26

The joint density function of two random variables X and Y is 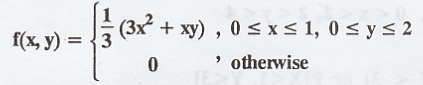 Find P [X + Y ≥ 1]

Solution:

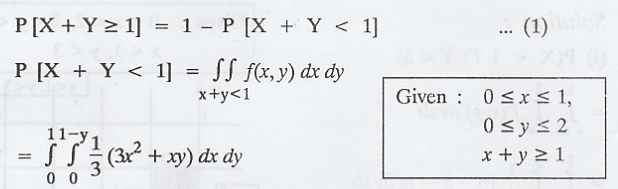
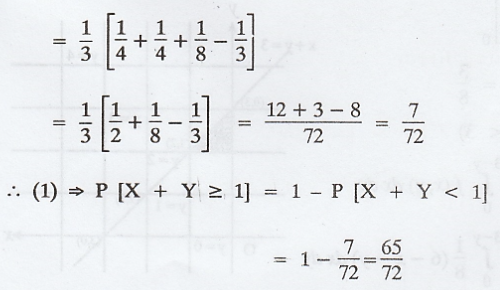
Example 2.1.29

If X and Y are two random variables having joint density function 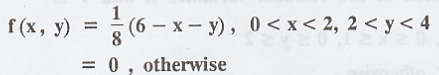 Find (i) P (X < 1 n Y < 3) or P[X < 1, Y < 3] (ii) P(X + Y < 3) (iii) P(X < 1 / Y < 3) [A.U N/D 2018 R-17 PS] [A.U A/M 2003, A.U M/J 2013] [A.U N/D 2017 R-13]

Solution :

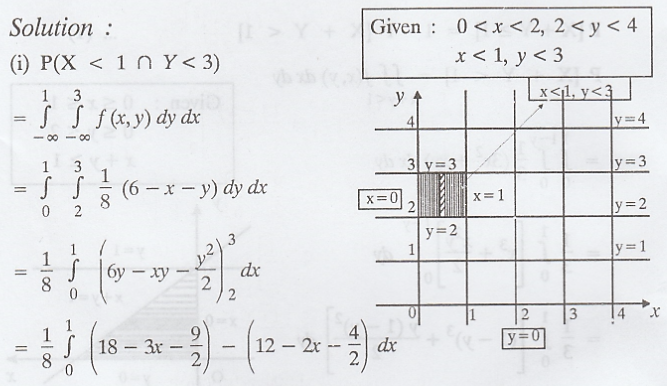
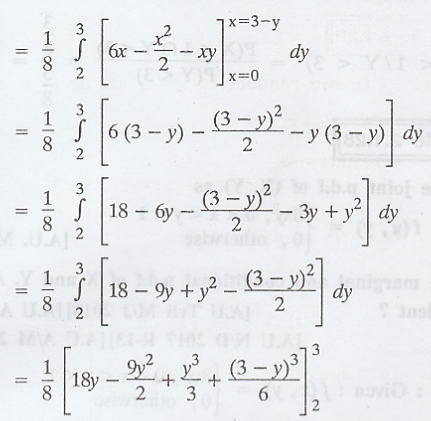
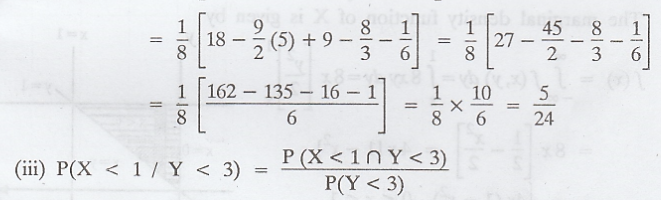
First let us find the marginal density function of Y

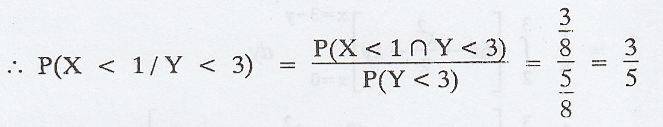
Example 2.1.28

Given the joint p.d.f of (X, Y) as 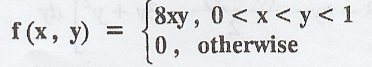 Find the marginal and conditional p.d.f of X and Y. Are X and Y independent? [A.U. M/J 2006, 2007] [A.U Tvli M/J 2010] [A.U A/M 2017 R-13] [A.U N/D 2017 R-13] [A.U A/M 2019 (R17) PS]

Solution :

Given: f(x, y) =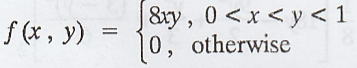 

The marginal density function of X is given by

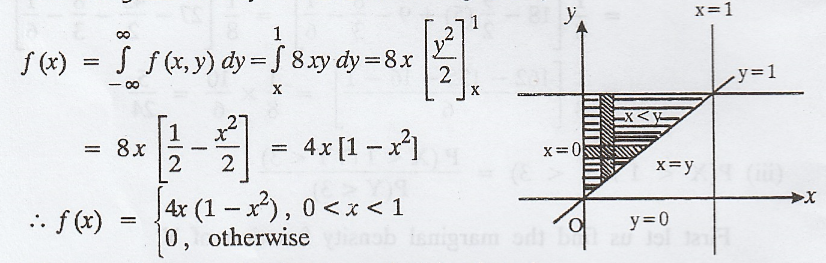
The marginal density function of Y is given by

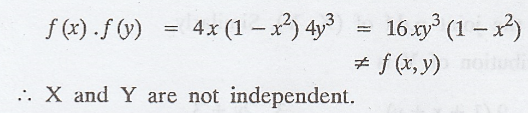
Example 2.1.29

The joint p.d.f of two random variables X and Y is given by  Find the marginal distributions of X and Y, the conditional distribution of Y for X = x and the expected value of this conditional distribution. [A.U Trichy M/J 2009][A.U. A/M 2004, A/M 2011]

Solution:

(i) The marginal distribution of X is

From the form of the joint p.d.f of (X, Y). Similarly,

The marginal distribution of Y is

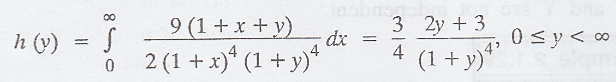
The conditional p.d.f of Y for X = x is

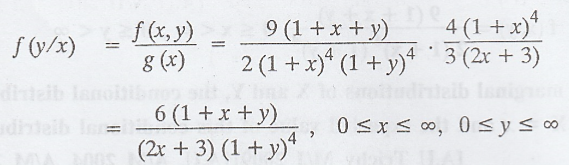
Conditional Expectation

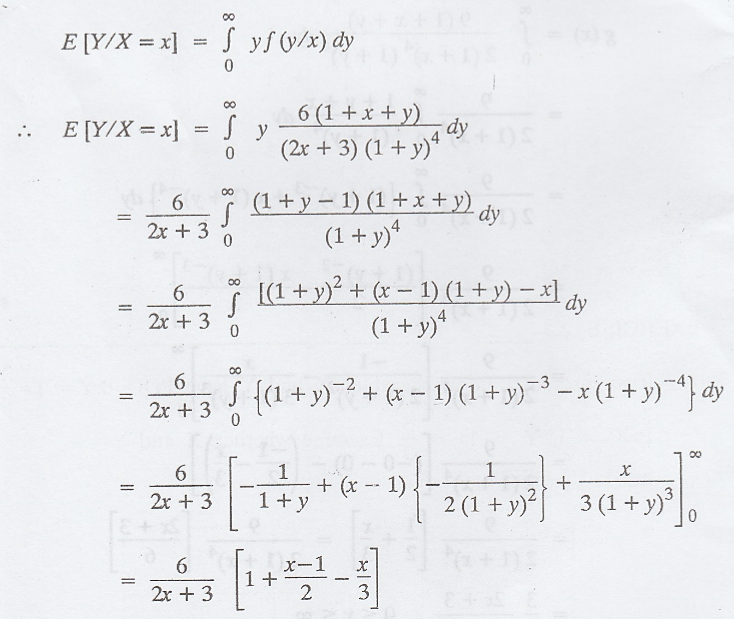
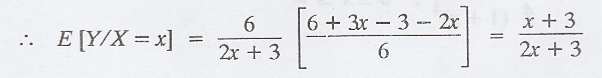
Example 2.1.30

Find k if the joint probability density function of a bivariate r.v. (X, Y) is given by f(x, y) =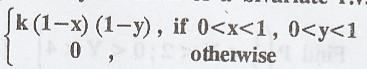 

[AU Dec. 2006, A/M 2008, Tvli A/M 2009, A.U A/M 2010, M/J 2014] [A.U N/D 2017 (RP) R-13]

Solution:

If f(x, y) is a joint p.d.f, then

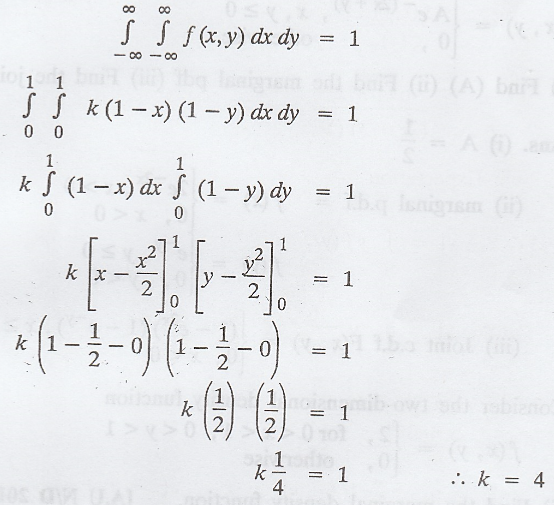
EXERCISE 2.1

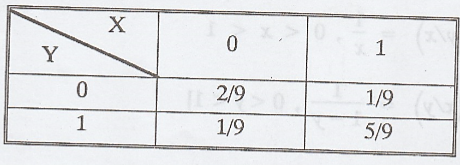
1. Two discrete random variables X and Y have P(X = 0, Y = 0) = 2/9. P(X = 1, Y = 1) = 5/9. Examine whether X and Y are independent.

Hint :

2. The density function of a two dimensional continuous random variables is given as f(x,y) = 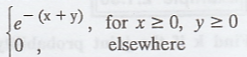 Find P(1/2 < X < 2 ; 0 < Y < 4)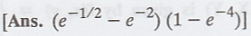 

3. Two r.v.'s X and Y have the joint p.d.f. 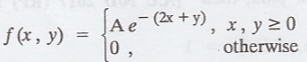 (i) Find (A) (ii) Find the marginal pdf (iii) Find the joint c.d.f.

[Ans. (i) A = 1/2 

(ii) marginal p.d.f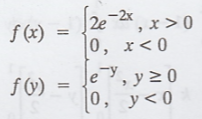  

(iii) Joint c.d.f F(x, y) = 

4. Consider the two-dimensional density function 

(i) Find the marginal density function.

(ii) Find the conditional density function.

5. Verify whether X and Y are statistically independent or not given 

[Ans. X and Y are not independent]

6. If X and Y have the j.p.d.f  Find (i) P(0 < x < 1/y = 2) (ii) P(X > Y) (iii) P(X + Y < 1)

[Ans. (i) 1 – 1/e, (ii)1/2, (iii) 1 – 2/e]

7. If f(x, y) =  (i) marginal probability functions (ii) conditional probability functions

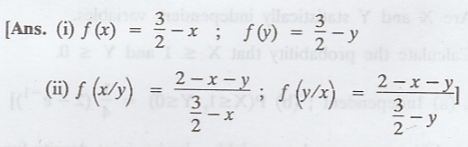
8. Let X₁ and X₂ be two r.v.'s with joint density function given by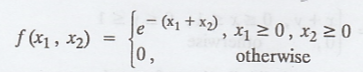 

Find the marginal densities of X₁ and X₂. Also find P(X₁ ≤ 1, X₂ ≤ 1) and P(X₁ + X₂ ≤ 1)

[Ans. Marginal density of X₁ is e^-x₁; Marginal density of X₂ is e^-x₂ 

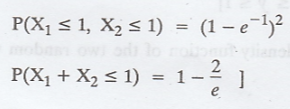
9. The joint probability function of two discrete r.v.'s X and Y is given by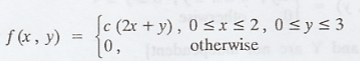 

(i) Find 'c'. (ii) Find P(X ≥ 1, Y ≤ 2) [Ans. (i) c = 1/21, (ii) P(X ≥ 1, Y = 2) = 8/21]

10. Test whether X and Y are independent or not. f(x, y) = 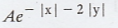 [Ans. independent]

11. The joint probability density of the r.v.'s X and Y is 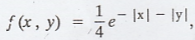 -∞ < x < ∞, -∞ < y < ∞.

(a) Are X and Y statistically independent variables.

(b) Calculate the probability that X ≤ 1 and Y ≤ 0.

[Ans. (a) Independent ; (b) P(X ≤ 1, Y ≤ 0) =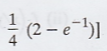 

12. If X and Y are two random variables, having joint density function 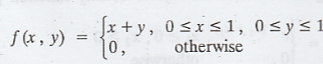 Determine the marginal distribution of x and y.

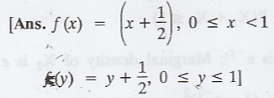
13. The Joint probability density function of the two random variables X and Y is given b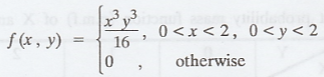y  Find the marginal density of X and Y.

14. The random variables X and Y have the j.p.d.f 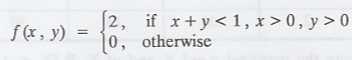 Find the conditional distribution of Y given X = x

15. Two random variables have the j.p.d.f given by 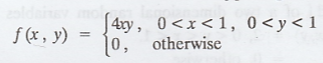 Show that X and Y are independent.

16. Let X and Y be two random variables with j.p.d.f 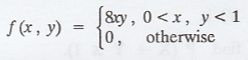 Find (i) the joint distribution function of X and Y, (ii) the marginal probability density of Y.

17. Let X and Y be jointly distributed with p.d.f.  Show that X and Y are independent.

18. If f(x, y) =  for 1 ≤ x < ∞ and 1/x < y < x is the j.p.d.f of the random variables X and Y, find (i) marginal distributions of X and Y. (ii) the conditional distribution of Y given X = x.

19. The joint probability mass function (p.m.f) of X and Y is

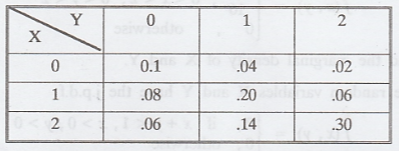
Compute the marginal p.m.f X and of Y, P [X ≤ 1, Y ≤ 1] and check if X and Y are independent. [A.U N/D. 2004]

20. If the joint p.d.f of a two dimensional random variables (X, Y) is given by  Find the marginal density function of X and Y. Also find X and Y are independent. [A.U. A/M. 2003] 

21. If the joint p.d.f of (X, Y) is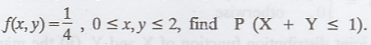 

22. If the joint p.d.f of a two dimensional random variables (X, Y) is given by 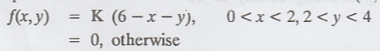 Find (i) the value of K (ii) P(X < 1, Y < 3); (iii) P(X + Y < 3) and (iv) P(X < 1 / Y < 3) [A.U. 2003] [A.U CBT Dec. 2009] [AU N/D 2009]

23. Find 'k' if the joint probability density function of a bivariate random variable (X, Y) is given by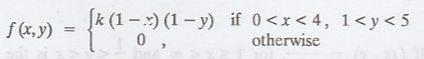 

24. Find k if the bivariate random variable X and Y has the p.d.f f(x, y) =kx² (8-y), x < y < 2x, 0 ≤ x <2

25. If X and Y have joint p.d.f f (x,y) = 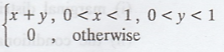 Check whether X and Y are independent.

26. Find the marginal density functions of X and Y, if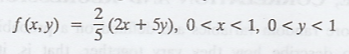 

27. The joint p.d.f of the two dimensional random variable is 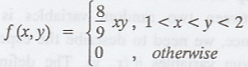 (i) Find the marginal density functions of X and Y.

(ii) Find the conditional density function of Y given X = X

28. The joint p.d.f of X and Y is given by 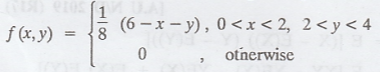 Find f(y/x=2)

29. The joint p.d.f of a two dimensional random variable (X, Y) is given by 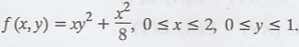 Compute (i) P (X > 1 / Y < 1/2) (ii) P [Y < 1/2 / X > 1](iii) P[X < Y] (iv) P[X + Y = 1]

30. The joint p.d.f of a bivariate R.V (X, Y) is given by 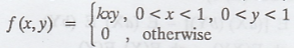 (i) Find k (ii) Find P (X + Y < 1) (iii) Are X and Y independent random variables

31. Let X and Y be two random variables with the joint p.d.f 

(i) Find the marginal p.d.f of X and Y (ii) Find P [X < 1/4 / 1/2 < Y < 3/4] (iii) Check X and Y are independent (iv) Find E[X] and E[Y]