Random Process and Linear Algebra: Unit I: Probability and Random Variables,,
Problems on Not Mutually Exclusive Independent Events
Important problems under (i) P(AUB) = P(A) + P(B) - P(A∩B) (ii) P(A∩B) = P(A) . P(B)
Type (1) (c) Not mutually exclusive, independent events
(i) P(AUB) = P(A) + P(B) - P(A∩B)
(ii) P(A∩B) = P(A) . P(B)
Example 1.1.16
A coin is biased so that a head is twice
as likely to occur as a tail. If the coin is tossed 3 times, what is the
probability of getting 2 tails and 1 head.
Solution:
The sample space S = {HHH, HHT, HTH,
THH, HTT, TTH, THT, TTT}
Since a coin is biased and a head is
twice as likely to occur as a tail, P(H) = 2/3, and P(T) = 1/3
Let A be the event of getting 2 tails
and 1 head in the 3 tosses of the coin.
Then A = {TTH, THT, HTT}
The outcomes of the 3 tosses are independent,
P(TTH) = P(T∩T∩H) = P(T) P(T) P(H) =
(1/3)(1/3)(2/3) = 2/27
|||ly P(THT) = 2/27; P(HTT) = 2/27
Hence P(A) = (2/27) + (2/27) + (2/27) =
6/27 = 2/9
Example 1.1.17
A can hit a target in 4 out of 5 shots
and B can hit the target in 3 out of 4 shots. Find the probability that (i) the
target being hit when both try. (ii) the target being hit by exactly one
person.
Solution :
Let A, B the events
A hit the target P(A) = 4/5
B hit the target P(B) = 3/4
(i) The events A and B are not mutually
exclusive because both of them hit the target.
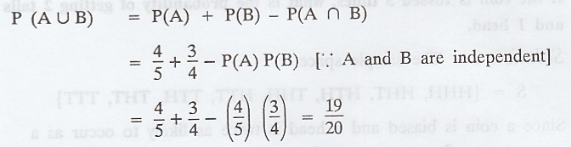
(ii) The target being hit by exactly one
person bas
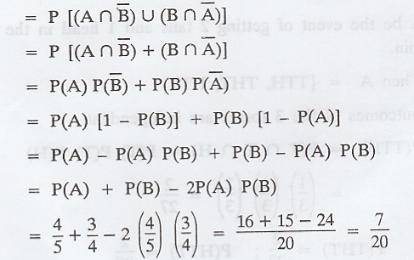
Example 1.1.18
A is known to hit the target in 2 out of
5 shots whereas B is known to hit the target in 3 out of 4 shots. Find the
probability of the target being hit when they both try?
Solution :
A -> be the event that 'A' hits the
target
B -> be the event that 'B' hits the
target
Given : P(A) = 2/5; P(B) = 3/4
To find P(AUB)
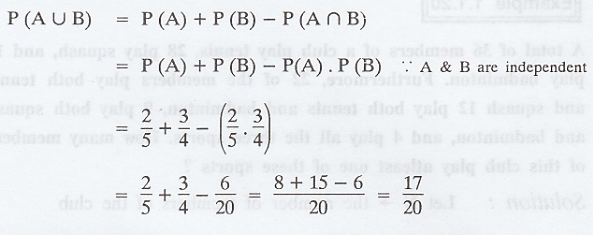
Example 1.1.19
One card is drawn from a deck of 52
cards. What is the probability of the card being either red or a king.
Solution:
Let A = {an event that the card drawn is
red}
B = {an event that the card drawn is
king}
AUB = {an event that a card to be either
red or a king}
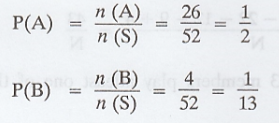
There are two red coloured king cards.
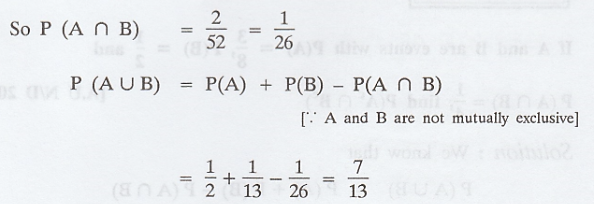
Example 1.1.20
A total of 36 members of a club play
tennis, 28 play squash, and 18 play badminton. Furthermore, 22 of the members
play both tennis and squash 12 play both tennis and badminton, 9 play both
squash and badminton, and 4 play all the three sports. How many members of this
club play atleast one of these sports?
Solution :
Let N -> the number of members of the
club
C -> any subset
P(C) = number of members in C / N
Now T -> set of members that plays
tennis
S -> set of members that plays squash
B -> set of members that plays
badminton
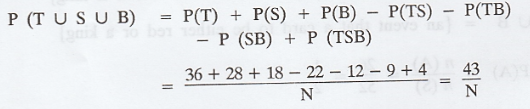
Hence we can conclude that 43 members
play atleast one of the sports.
Example 1.1.21
If A and B are events with P(A) = 3/8,
P(B) = 1/2 and P(A∩B) = 1/4, find P(AC∩BC) [A.U N/D 2006]
Solution:
We know that
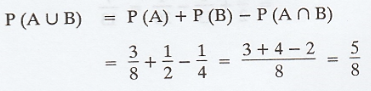
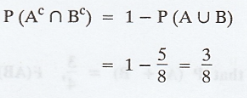
Example 1.1.22
If A and B are independent events with
P(A) = 0.4 and P(B) = 0.5 find P(A U B). [A.U. Dec, 96]
Solution
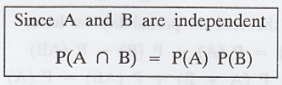

Example 1.1.23
Let events A and B be independent with
P(A) = 0.5 and P(B) = 0.8. Find the probability that neither of the events A
nor B occurs. [A.U. May 2000]
Solution :
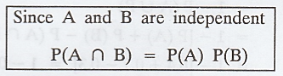

Example 1.1.24
Event A and B are such that P(A + B) =
3/4, P(AB) = 1/4 and P(Ā) = 2/3 find P(B). [A.U N/D 2004]
Solution :
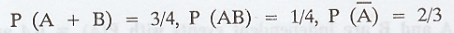
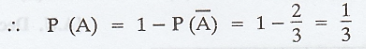
By the addition theorem on probability we have,
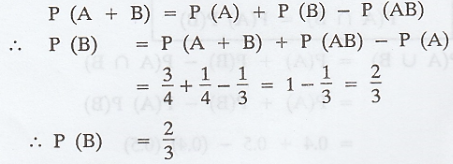
Example 1.1.25
If P(A) = 0.4, P(B) = 0.7 and P(A∩B) =
0.3 find the probability that neither A nor B occurs.
Solution :
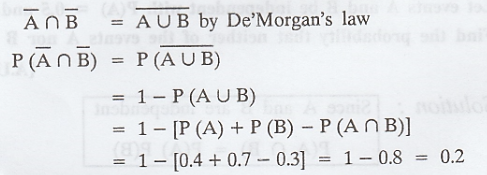
Example 1.1.26
If you twice a flip a balanced coin,
what is the probability of getting atleast one head ?
Solution:
When we flip a balanced coin, the sample
space will be,
S = {HH, HT, TH, TT}
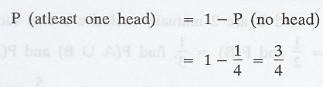
Example 1.1.27
Prove that for any event A in S, P(A∩Ā)
= 0
Solution :
We know that P(S) = 1 and A ∩ Ā = S
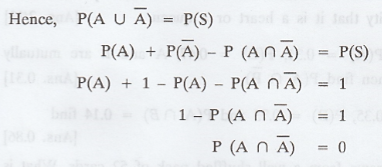
EXERCISES 1.1
1. State the axioms of probability
2. Define mutually exclusive events with
an example.
3. Out of 50 students in a class, what
is the probability of a single student to opt for a picnic. [Ans. 0.02]
4. What is the probability of obtained two heads in two throws of a single coin? [Ans. 1/4]
5. What is the probability of picking an
ace and a king from a deck of 52 cards?[Ans. 8/663]
6. From a bag containing 3 red and 2
black balls, 2 balls are drawn at random. Find the probability that they are of
the same colour. [Ans. 2/5]
7. Prove that the probability of an impossible event is zero.
8. When A and B are 2 mutually exclusive
events such that P(A) = 1/2 and P(B) = 1/3,
find P(AUB) and P(A∩B). [Ans. P(AUB) =
5/6, P(A∩B) = 0]
9. A fair coin is tossed 5 times what is
the probability of having atleast one head ? [Ans. 31/32]
10. A card is drawn at random from a
well shuffled pack, what is the probability that it is a heart or a queen.
[Ans. 2/13]
11. Given that P(A) = 0.31, P(B) = 0.47
A and B are mutually exclusive. Then find 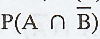 [Ans. 0.31]
[Ans. 0.31]
12. If P(A) = 0.35, P(B) = 0.73 and P(A∩B)
= 0.14 find 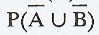 [Ans. 0.86]
[Ans. 0.86]
13. A card is drawn from a well shuffled
pack of 52 cards. What is the probability that it is either clever or king.
[Ans. 4/13]
14. If BCA, prove that 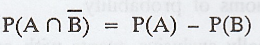
15. Given P(A) = 1/3, P(B) = 1/4 P(A∩B)
= 1/6, find the following probability 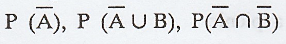
16. If A and B are two independent
events then 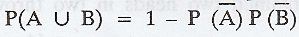
17. It is given that P(A U B) = 5/8, P(A∩B)
= 1/3 and 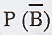 = 1/2. Show that the events A and B are independent.
= 1/2. Show that the events A and B are independent.
18. Given P(A) = 0.35, P(B) = 0.73 and
P(A∩B) = 0.14, find (a)P(AUB) (b)P(A∩B) 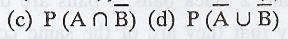
19. Given P(A) = 0.3, P(B) = 0.5 and P(A∩B)
= 0.24 find 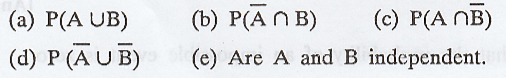
Random Process and Linear Algebra: Unit I: Probability and Random Variables,, : Tag: : - Problems on Not Mutually Exclusive Independent Events
Related Topics
Related Subjects
Random Process and Linear Algebra
MA3355 - M3 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
