Signals and Systems: Unit IV: Analysis of Discrete Time Signals,,
Problems Based on Properties of DIFT
Anna university important Problems based on Properties of DIFT
PROBLEMS BASED ON PROPERTIES OF DTFT
Problem 1:
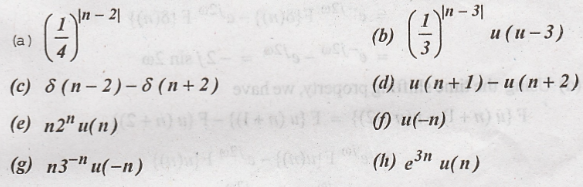
Solution:
(a)
Using the time shifting property, we have
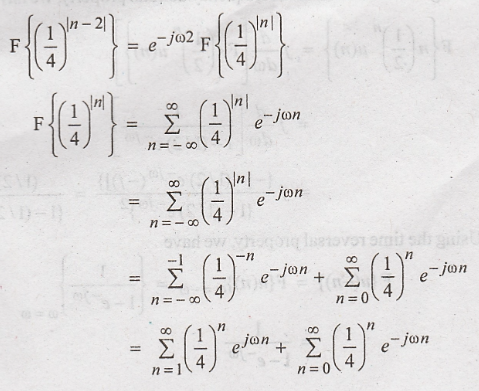
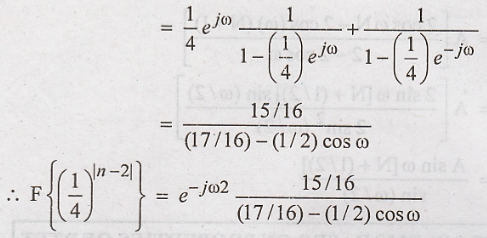
(b)
Using the time shifting property, we have
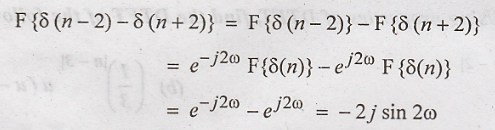
(d)
Using the time shifting property, we have
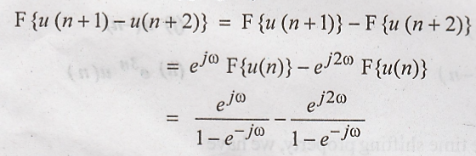
(e)
Using differentiation in the frequency domain property, we have
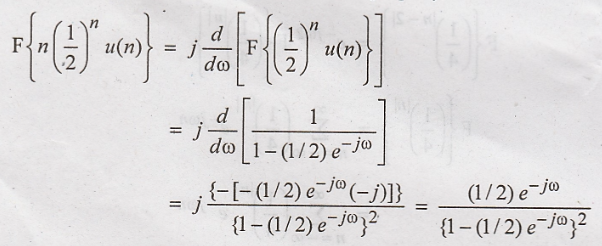
(f)
Using the time reversal property, we have
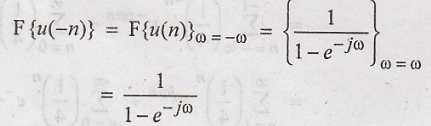
(g)
Using differentiation in frequency domain and time reversal properties, we have
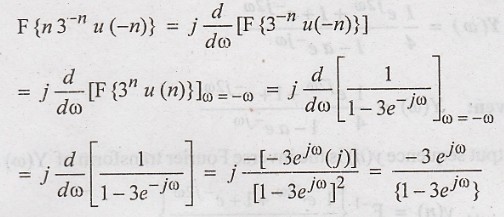
(h)
Using the frequency shifting property, we have
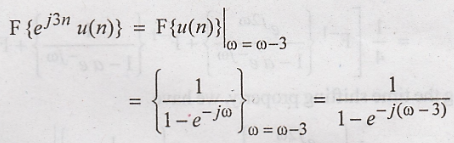
Problem 2:
Find
the inverse Fourier transform for the first order recursive filter
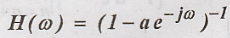
Solution:
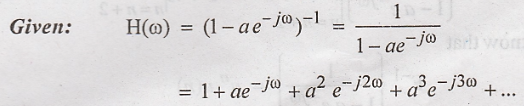
Let
h(n) be the inverse Fourier transform of H(ω)
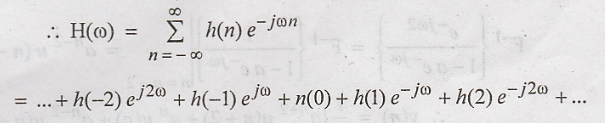
On
comparing the two expressions for H(ω). We can say that the samples of h(n) are
the co-efficients of e –j ω n
h(n)
= {1, a, a2, a3 ..., ak,...}
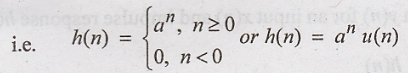
Problems 3:
Determine
the output sequence from the output spectrum:
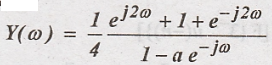
Solution:
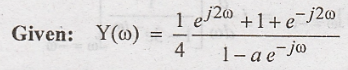
The
output sequence y(n) is the inverse Fourier transform of Y(ω).
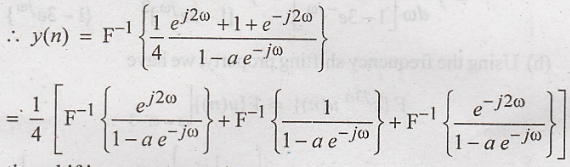
Using
the time shifting property, we have
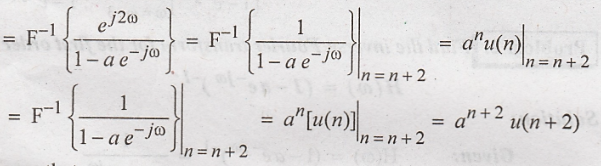
Also
we know that
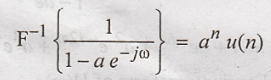
Using
the time shifting property, we have
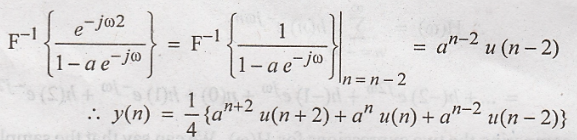
Problem 4:
The
impulse response of a LTI system is h(n) = {1, 2, 1, -3}. Find the response of
the system for the input x(n) = {1, 3, 2, 1}.
Solution:
The
response of the system y(n) for an input x(n) and impulse response h(n) is
given by
y(n)
= x(n) * h(n)
Using
the convolution property of Fourier transform, we get
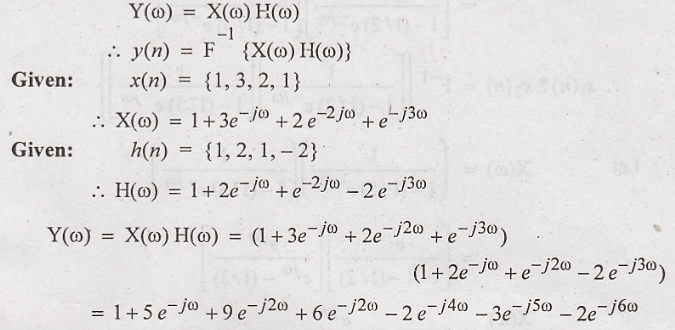
Taking
inverse fourier transform on both sides, we get
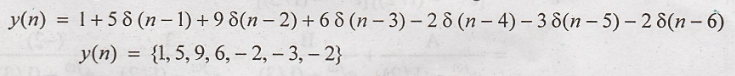
Problem 5:
Find
the Convolution of the signals given below using Fourier transform:
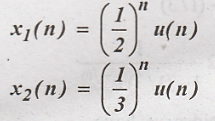
Solution:
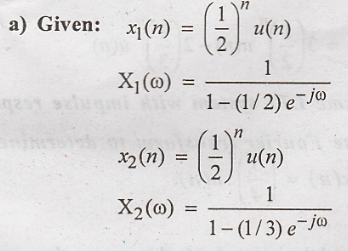
Using
the convolution property of Fourier transform we get
F[x1(n)
* x2(n)] = X1(ω) X2(ω)

Taking
inverse Fourier transform on both sides, we have.
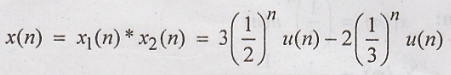
Problem 6:
Consider
a discrete time LTI system with impulse response h(n) = (1/2)n u(n).
Use Fourier transform to determine the response to the signal x(n) = (3/4)n
u(n).
Solution:
Given
the impulse response h(n) and the input x(n) to the system, the response y(n)
in given by
y(n)
= x(n) * h(n)
Using
the convolution property of Fourier transform we have
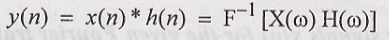
Where
X(ω) and H(ω) are the Fourier transforms of x(n) and h(n) respectively
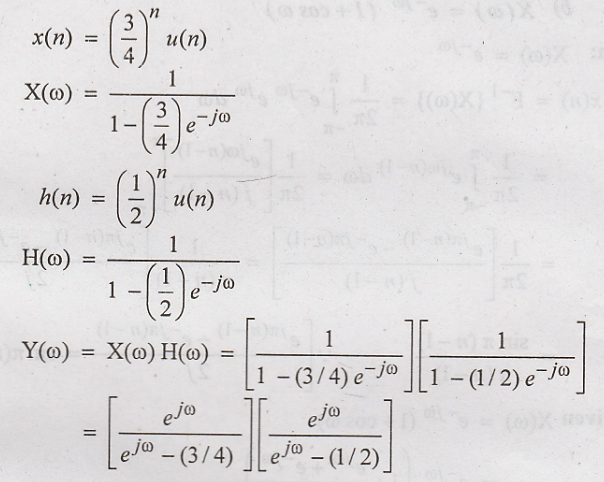
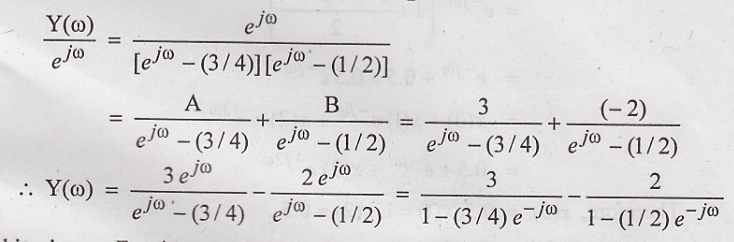
Taking
inverse Fourier transform on both sides, we get the response
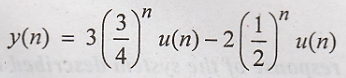
Signals and Systems: Unit IV: Analysis of Discrete Time Signals,, : Tag: : - Problems Based on Properties of DIFT
Related Topics
Related Subjects
Signals and Systems
EC3354 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
