Problems Based on Laplace Transform Analysis of CT System

Problems Based on Laplace Transform Analysis of CT System.

Problem 1:

The tranafer function of the system is given as H(s) =  Determine the impulse response if the system is (i) stable (ii) causal. Whether this system will be stable and causal simultaneously?

Solution:

This system has 2 poles. They are s = -3 and s = 2. One pole lies on the right side and another pole on the left side. Hence the system cannot be causal and stable simultaneously. Impulse response for stable system.

For stable system ROC of H(s) must include jo axis of s plane.

In the above figure, pole at s = 2 lies on right side of Roc. Hence corresponding time domain signal will be left sided.

Then pole s = -3 lies on left half of Roc. Hence corresponding time domain signal will be right sided.

Hence impulse response becomes

(ii) Impulse response of causal system.

For causal system all the poles must lies on left side of Roc.

Here both the poles lie on left side of Roc. Hence time domain, signal will be right sided, 

Roc: Re(s) > 2. Hence impulse becomes h(t) = e^-3t(t) + e^2t u(t).

Problem 2:

Determine the impulse response h(t) of the system given by the differential equation  with all initial conditions to be zero.

Solution:

Taking Laplace transform of given differential equation.

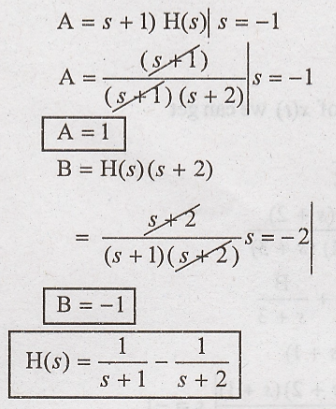
Take inverse laplace transform of above equation,

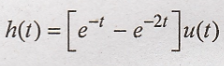
Problem 3:

A stable system has the input x(t) and output y(t). Use Laplace transform to determine the transfer function and impulse response h(t) of the system given x(t) = e^-2t u(t); and y(t) = -2e^-t u(t) + 2e^-3t u(t).

Solution:

(i) Transfer function:

System transfer function

H(s) = Y(s) / X(s)

By taking laplace transform of x(t) we can get

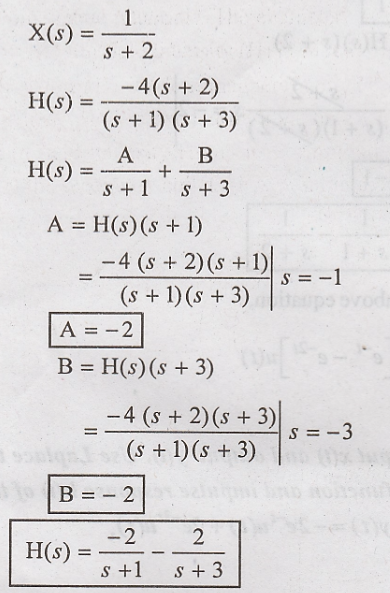
(ii) To obtain impulse response of stable system.

ROC of Re(s) > -1 includes Re(s) > -3 and jω axis of s plane. Inverse laplace transform of H(s) gives.

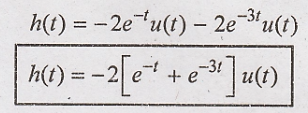
Problem 4:

The input and output of a causal LTI system are related by the differential equation.  Find impulse response of the system. [May 11 - Marks 8]

Solution:

Talking Laplace transform

Take inverse laplace transform,

Problem 5:

Solve the differential equation 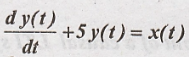 with initial condition y(o⁺) = -2 and input x(t) = 3e^-2t u(t).

Solution:

Taking Laplace trans form on both sides,

But we know that

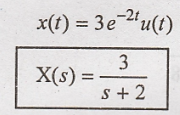
Now substitute X(s) in (1)

Taking inverse Laplace transform

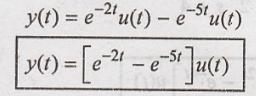
Problem 6:

Solve the following differential equation  

Solution:

Taking Laplace transform of given differential equation.

Take partial fraction on above equation.

Taking inverse Laplace transform of above equation.

Problem 7:

The circuit shown in figure 3.34 represents a system with input x(t) and output y(t). Determine response of the system y(t) using Laplace transforms, given R = 3Ω, L = 1H, C= 1/2. Farad, x(t) = u(t), the current through the inductor at t = 0^- is 2A. And the voltage across the capacitor at t = 0^- is IV. [May 09-8 Marks]

Solution:

By Application KVL to the laplace equivalent circuit.

Substitute (2) in (1)

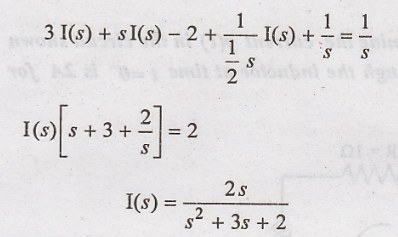
But voltage across inductor will be

Substitute the values in above equation.

Taking inverse laplace transform

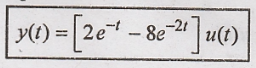
Problem 8:

Use Laplace transform to determine the current y(t) in the circuit shown in figure3.36. The current through the inductor at time t = 0^- is 2A for (i) x(t) = e^-t u(t) (ii) x(t)= cost u(t).

Solution:

Applying KVL to the circuit

case I:

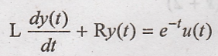
Taking Laplace transform

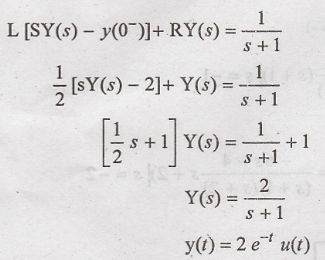
(ii) x(t) = cost u(t)

Applying KVL to the circuit

Taking Laplace transform.

Taking inverse Laplace transform of above equation

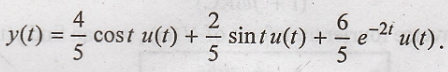
Problem 9:

The input voltage to the RC circuit is given as 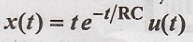 and the impulse response of this circuit is given by 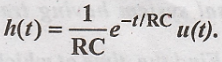 Find out out the out put y(t)

Solution:

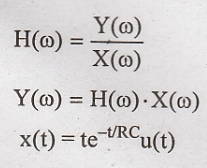
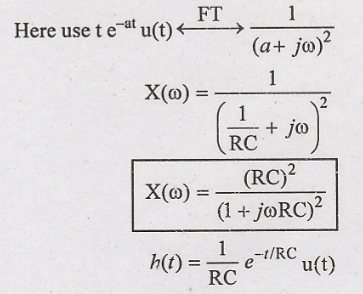
Taking inverse fourier transform of Y(ω), we can find y(t)

Problem 10:

A causal system having transfer function H(s) = 1/s+4 is excited with x(t) = 5u(t). Find the time at which output reaches 90% of its steady state value.

Solution:

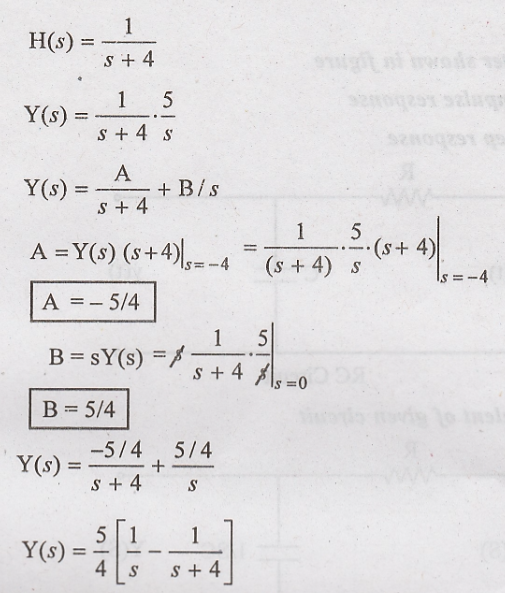
Taking Inverse Laplace transform of above equation

Steady state volume is obtained as

Hence 90% of above steady state value is 

Substitute this value for y(t) in (1)

Problem 11:

For the RC filter shown in figure

(i) Obtain impulse response

(ii) Obtain step response

Laplace equivalent of given circuit

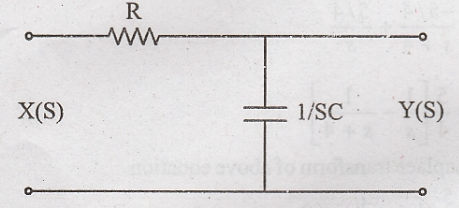
(i) Impulse response:

Apply voltage divider formula in Laplace equivalent circuit, we can write 

(ii) Step response:

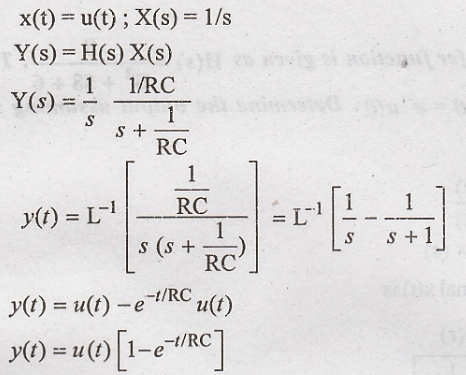
Problem 12:

Find the impulse response of the system given by 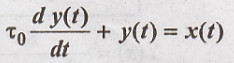 May 2002/8marks

Solution:

The given differential equation is,

Taking Laplace transform of above equation

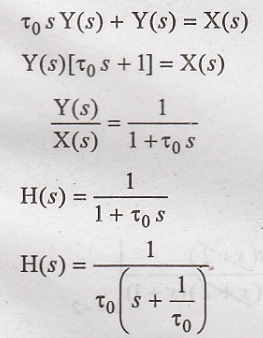
Taking inverse Laplace transform of a above equation

Problem 13:

The system transfer function is given as 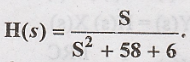 The input to the system is x(t) = e^-t u(t). Determine the output assuming zero initial conditions.

Solution:

The given input signal x(t) is

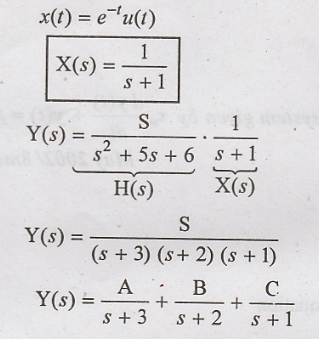
Taking inverse laplace transform on both sides

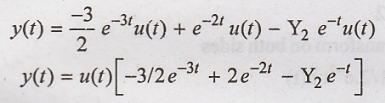
Problem 14:

Find the steady state response of the following systems to unit step excitations

Solution :

(i) H(s) = 1/S+1

Y(s) is calculated for the unit step input

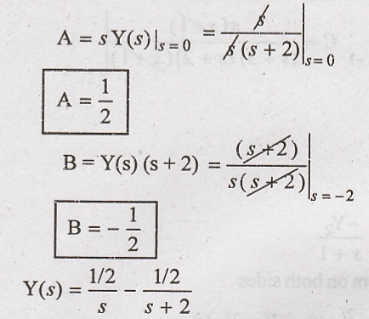
Taking inverse Laplace transform on both sides

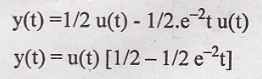
(ii) 

Solution

Y(s) is calculated for the unit step input u(t)

Taking Laplace transform on the sides

Problem 15:

The impulse response of the system is given as  Determine the transfer function of the inverse system.

Solution:

The given impulse response is

By taking Laplace transform.

The transfer function of the inverse system is given as

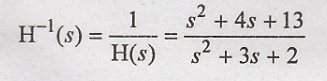
Problem 16:

Find the step response of the system whose impales response is given as h(t) = u(t + 1)- u(t − 1) [Dec-11/4 marks]

Solution:

Impulse response is given as h(t) = u(t+1)-a(t-1)

Taking Laplace transform of given impulse response.

Input is unit step signal, hence X(s) = 1/s

Taking inverse Laplace transform of above equation.