Poisson Process

POISSON PROCESS [Continuous time Markov Chain]

Definition : [A.U. May 1999, N/D 2010, CBT A/M 2011] [A.U Tvli A/M 2011, CBT N/D 2011]

If X(t) represents the number of occurrences of a certain event in (0, t), then the discrete random process {X(t)} is called the Poisson process, provided that the following postulates are satisfied.

(i) P[1 occurrence in (t, t+∆t)] = λ ∆t + 0 (∆t)

(ii) P [0 occurrence in (t,t+t∆)] = 1 - λ ∆t + 0 (∆t)

(iii) P [2 or more occurrences in (t, t+∆t)] = 0 (∆t)

(iv) X(t) is independent of the number of occurrences of the event in any interval prior and after the interval (0, t).

(v) The probability that the event occurs a specified number of times in (t₀, t₀+t) depends only on t, but not on to.

Poisson process is not a stationary process, as its statistical properties (mean, autocorrelation, ...) are time dependent.

Mean and Variance of the Poisson Process: [A.U A/M 2003]

The probability distribution of the Poisson process X(t) is given by,

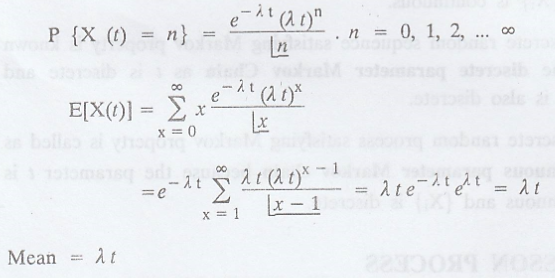
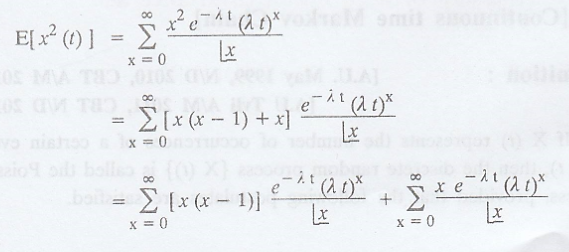
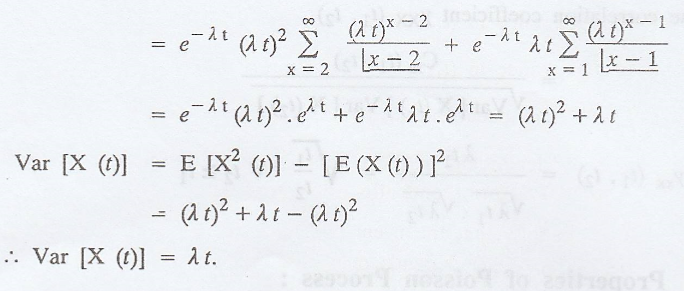
Autocorrelation of Poisson Random Process :

[A.U M/J 2014, A.U A/M 2015 (RP) R8, A.U M/J 2016 PQT R13] [A.U A/M 2018 R-13]

Let R_XX (t₁, t₂) is defined as the autocorrelation at time interval (t₁, t₂).

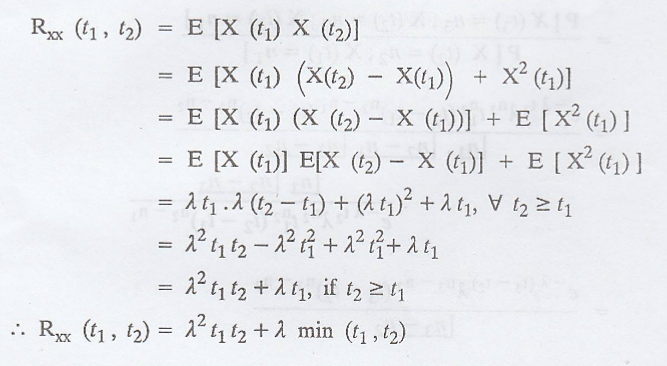
Relationship between mean, covariance and autocorrelation of Poisson process

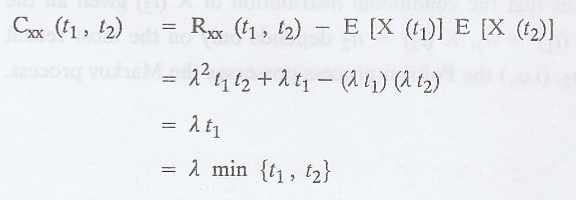
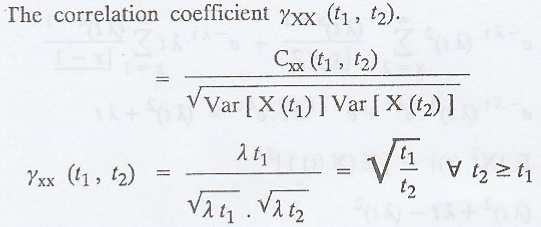
Properties of Poisson Process :

i. The Poisson process is a Markov process : [A.U M/J 2013] A.U. M.E. June 2010 [A.U M/J 2013, N/D 2013] [A.U A/M 2018 R-08]

Let us consider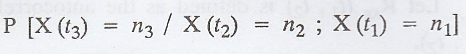 

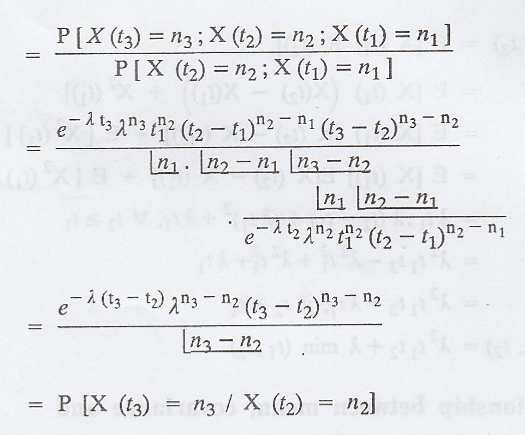
This means that the conditional distribution of X(t₃) given all the past values X(t₁) = n₁, X(t₂) = n₂ depends only on the most recent value X(t₂) = n₂. (i.e.,) the Poisson process possesses the Markov process.

ii. The sum of two independent Poisson process is again a Poisson process. (Additive property)

[OR]

If {X₁(t)} and {X₂(t)} are two independent Poisson process with parameters λ₁ and λ₂ respectively, show that the process {X₁(t) + X₂(t)} is also a Poisson process.

[A.U. N/D 2006, N/D 2013, A/M 2014, A/M 2015 (RP) R-8] [A.U Trichy A/M 2010, CBT M/J 2010, Tvli M/J 2010] [A.U CBT A/M 2011, Trichy M/J 2011] [A.U M/J 2016 R13 PQT] [A.U N/D 2019 R-17 RP, PQT] [A.U A/M 2019 R17 PQT] [A.U A/M 2019 (R8) RP]

Proof :

Let X(t) = X₁(t) + X₂(t)

iii. The difference of two independent Poisson processes is not a Poisson process. [A.U. A/M 2004, N/D 2003, A/M 2011] [A.U Trichy A/M 2010, A.U Tvli M/J 2010, A.U Tvli. A/M 2011] [A.U M/J 2013] [A.U M/J 2016 R13 PQT] [A.U N/D 2019 R17 PQT]

Proof :

Let X(t) = X₁(t) + X₂(t)

Then E [X(t)] = E[X₁(t) - X₂(t)] = E[X₁(t)] - E[X₂(t)]

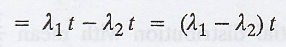
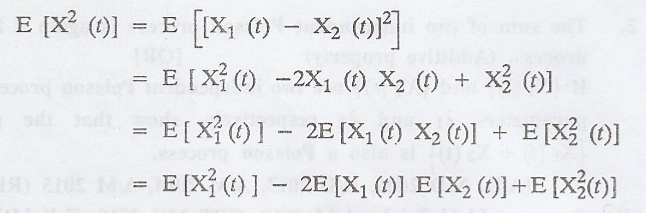
.'. X₁(t) and X₂(t) are independent.

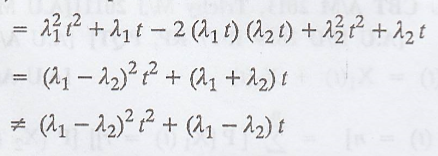
.'. X(t) = X₁(t) - X₂(t) is not a Poisson process.

iv. The inter arrival time of a Poisson process with parameter λ has an exponential distribution with mean 1/λ [A.U. A/M. 2004] [A.U N/D 2016 R13 PQT, A/M 2019 R17 RP, N/D 2019 R17 RP]

Proof:

Consider two consecutive occurences of the event E_i and E_i+1.

Let E_i takes place at time t_i and T, the interval between the occurrences E_i and E_i+1. T is a continuous R.V.

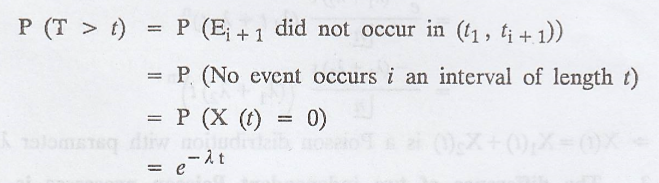
The c.d.f of T is given by

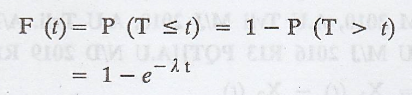
The p.d.f of T is given by f(t) = λe ^{– λ t}, t ≥ 0

This is a exponential distribution with mean 1/λ

v. If the no. of occurrences of an event E in an interval of length 't' is a process {X(t)} with parameter λt and if each occurrence of E has a constant probability 'p' of being recorded and the recording are independent of each other, then the number N(t) of the recorded occurrences in t is also a Poisson process with parameter λp. [A.U. A/M. 2004]

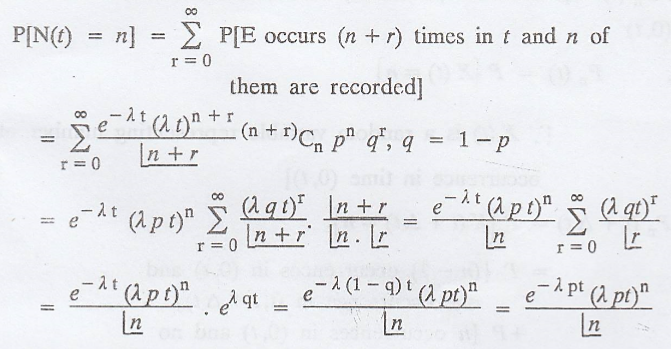
=> N(t) is a Poisson random process.

If {X(t)} is a Poisson process, prove that

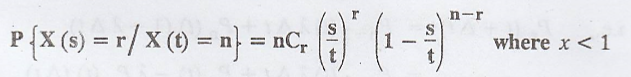
Proof

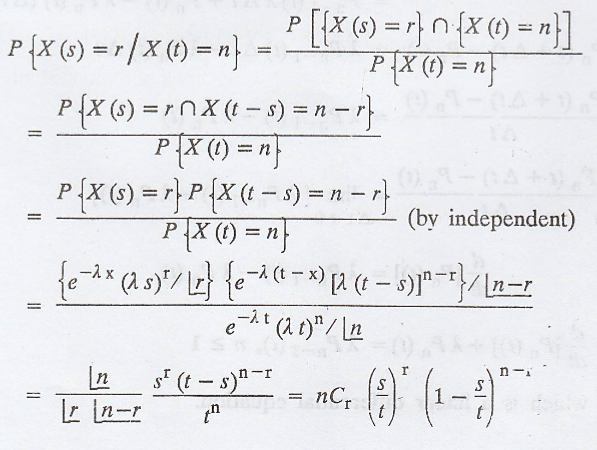
Derivation of the probability law (or probability function or probability distribution) for the Poisson process X(t). [A.U A/M 2011] [A.U N/D 2019 R17 PQT]

Let λ be the number of occurrences of the event in unit time.

Let P_n(t) represent the probability of n occurrences of the ever n (0,t)

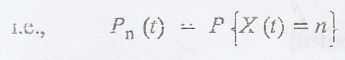
['.' X(t) is a random variable representing number of occurrence in time (0,t)]

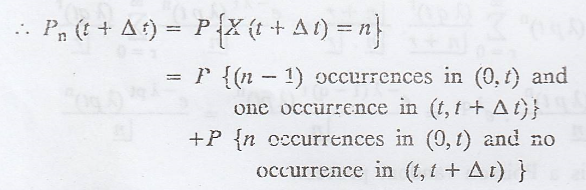
[by the postulates of Poisson process neglecting 0 (∆t)]

which is a linear differential equation.

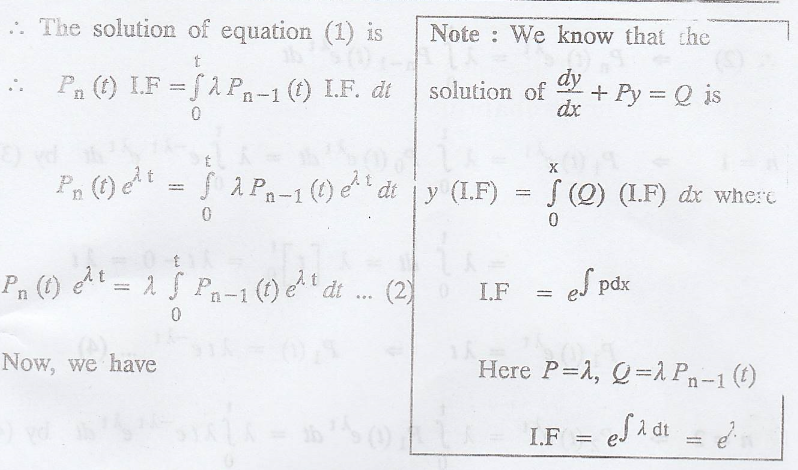
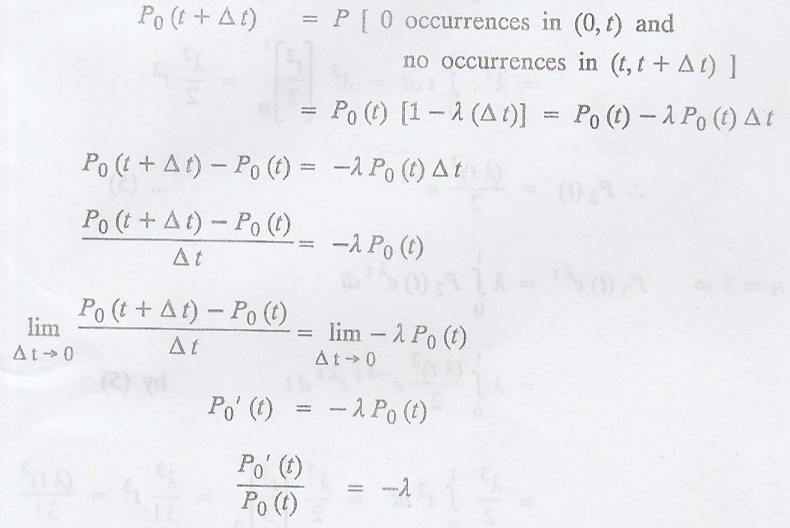
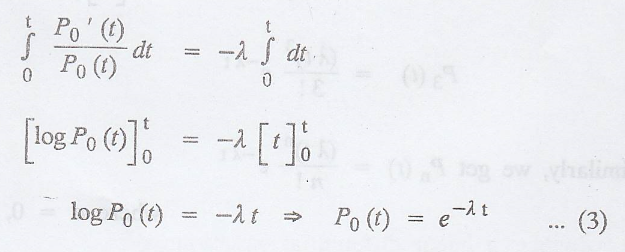
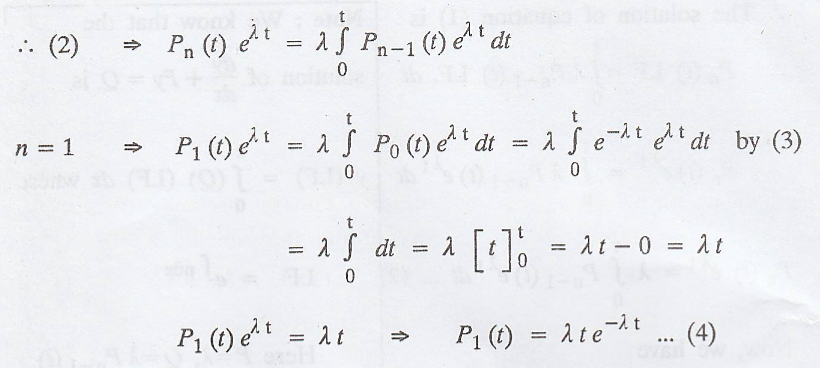
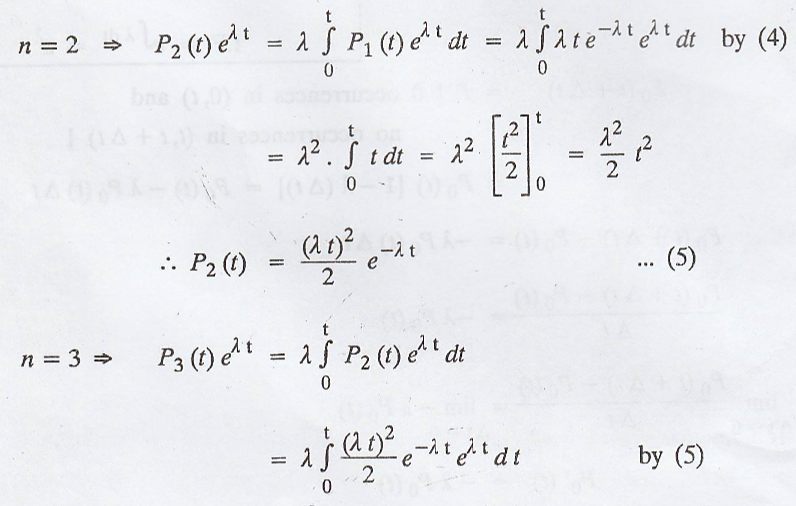
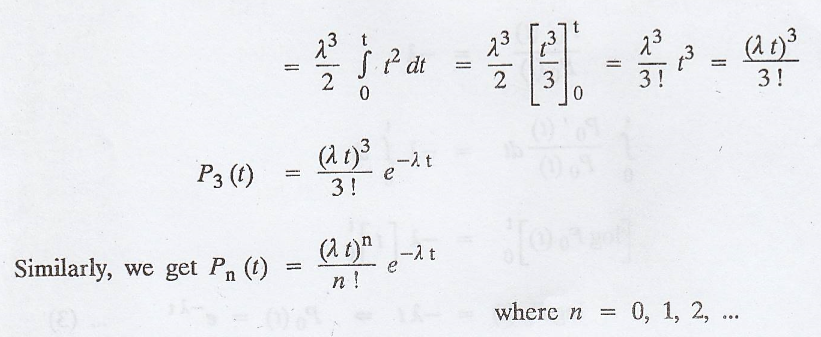
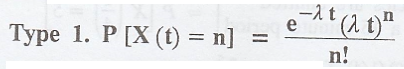
Example 3.6.1

If patients arrive at a clinic according to Poisson process with mean rate of 2 per minute. Find the probability that during a 1-minute interval, no patient arrives. [A.U A/M 2017 R-13 RP]

Solution :

Let X(t) be the number of patients arrive at a clinic in the time interval of t.

Given:

Mean rate, λ = 2 per minute

Time interval, t = 1 per minute

No. of arrivals, n = 0

X(t) follows a Poisson process, P[X(t) = n] = e ^{– λ t} (λt) ⁿ / n!

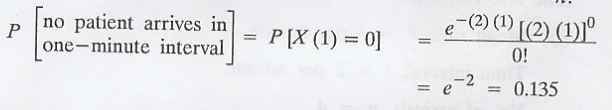
Example 3.6.2

If particles are emitted from a radio active source at the rate of 20 per hour, find the probability that exactly 5 particles are emitted during a 15 minute period. [A.U CBT A/M 2011]

Solution :

Let X(t) be the number of particles are emitted in the time interval of t.

Given:

Mean rate, λ = 20 per hour

Time interval, t = 15 min = 15/60 hrs = 1/4 hrs.

No. of arrivals, n = 5

X(t) follows a Poisson process, P[X(t) = n] = e ^{– λ t} (λt) ⁿ / n!

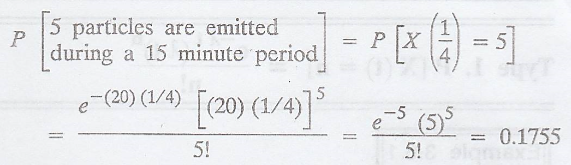
Example 3.6.3

Suppose that customers arrive at a bank according to a poisson process with a mean rate of 3 per minute; find the probability that during a time interval of 2 min (i) exactly 4 customers arrive and (ii) more than 4 customers arrive. (iii) fewer than 4 customer in 2 minute interval. [A.U M/J 2009, CBT N/D 2011, M/J 2012, M/J 2013] [A.U N/D 2013, A/M 2015 R-8, N/D 2015, R13 PQT] [A.U N/D 2015, R13 RP] [A.U A/M 2017 R-08]

Solution :

Let X(t) be the number of customers arrive at a bank in the time interval of t.

(i) Mean rate, λ = 3 per minute

Time interval, t = 2 per minute

No. of arrivals, n = 4

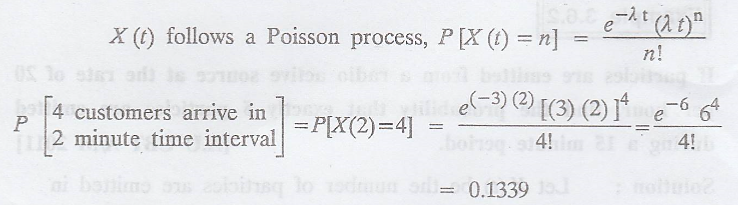
(ii) Mean rate, λ = 3 per minute

Time interval, t = 2 per minute

No. of arrivals, n = more than 4.

P[more than 4 customers in 2 min. interval]

= P[X(2) > 4] = 1 - P[X(2) ≤ 4]

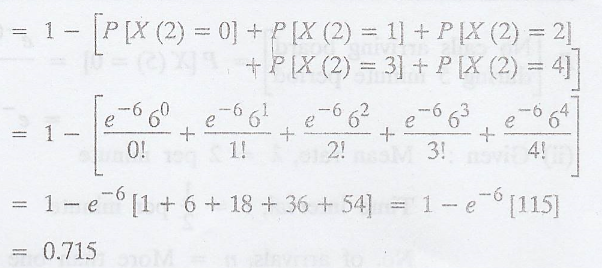
(iii) Mean rate, λ = 3 per minute

Time interval, t = 2 per minute

No. of arrivals, n = fewer than 4

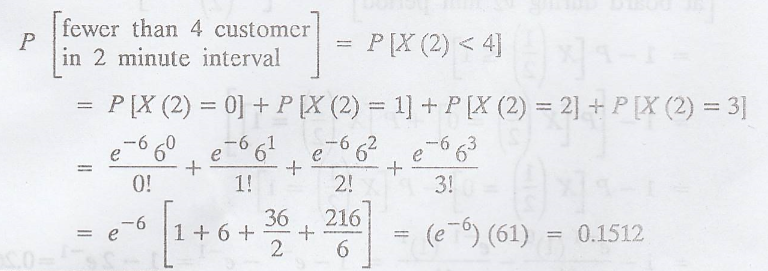
Example 3.6.4.

The number of telephone calls arriving at a certain switch board within a time interval of length (measured in minutes) is a Poisson process X(t) with parameter λ = 2. Find the probability of (i) No telephone calls arriving at this switch board during a 5 minute period. (ii) More than one telephone call arriving at this switch board during a given 1/2 minute period. [AU Model]

Solution :

Let X(t) be the number of calls arrive at a board in the time interval of t.

(i) Given: Mean rate, λ = 2 per minute

Time interval, t = 5 per minute

No. of arrivals, n = 0

X(t) is a Poisson process, P[X(t) = n] = e ^{– λ t} (λt) ⁿ / n!

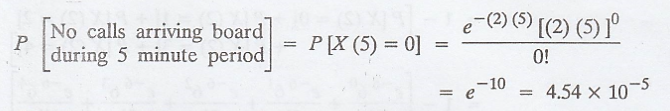
(ii) Given: Mean rate, λ = 2 per minute

Time interval, t = 1/2 per minute

No. of arrivals, n = More than one call

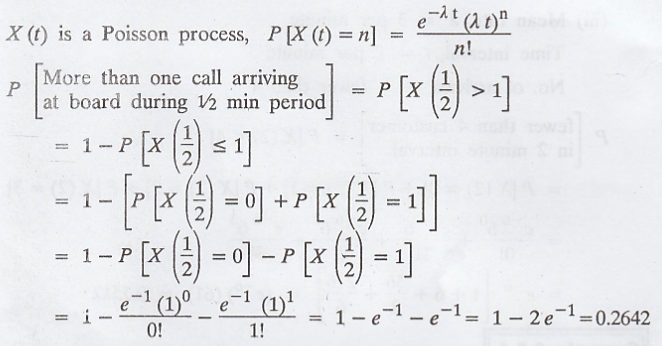
Example 3.6.5

Queries presented in a computer data base are following a Poisson process of rate λ = 6 queries per minute. An experiment consists of monitoring the data base for m minutes and recording N(m) the number of queries presented.

(1) What is the probability that no queries arrive in one minute interval ?

(2) What is the probability that exactly 6 queries arriving in one minute interval?

(3) What is the probability of less than 3 queries arriving in a half minute interval ? [A.U. M/J 2007]

Solution :

Let N(m) (or) X(t) be the number of queries presented in m (or) t minutes.

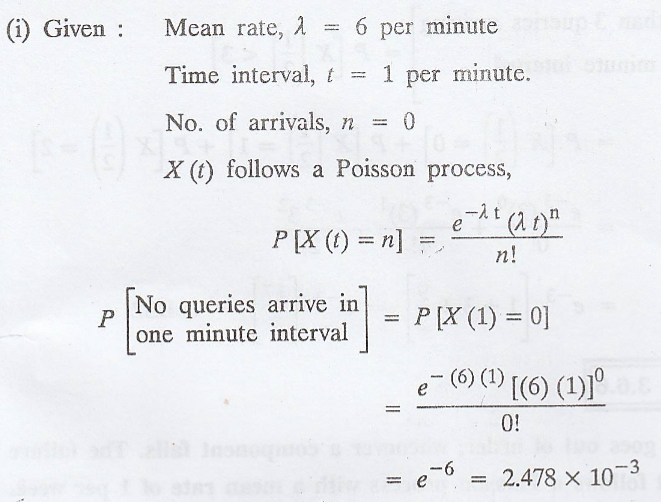
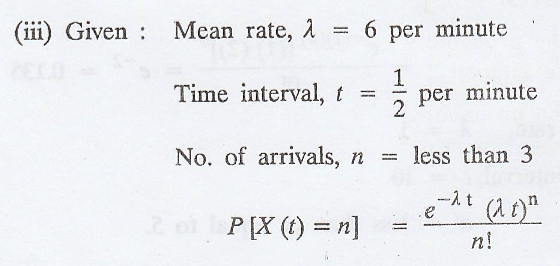
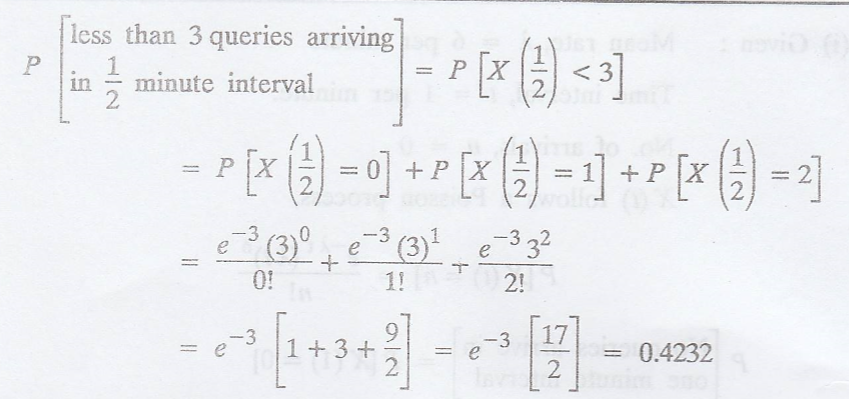
Example 3.6.6

A machine goes out of order, whenever a component fails. The failure of this part follows a Poisson process with a mean rate of 1 per week. Find the probability that 2 weeks have elapsed since last failure. If there are 5 spare parts of this component in an inventory and that the next supply is not due in 10 weeks, find the probability that the machine will not be out of order in the next 10 weeks. [A.U M/J 2009] [A.U N/D 2018 R13 PQT]

Solution :

(i) Given:

 Mean rate, λ = 1

Time interval, t = 2

n = 0

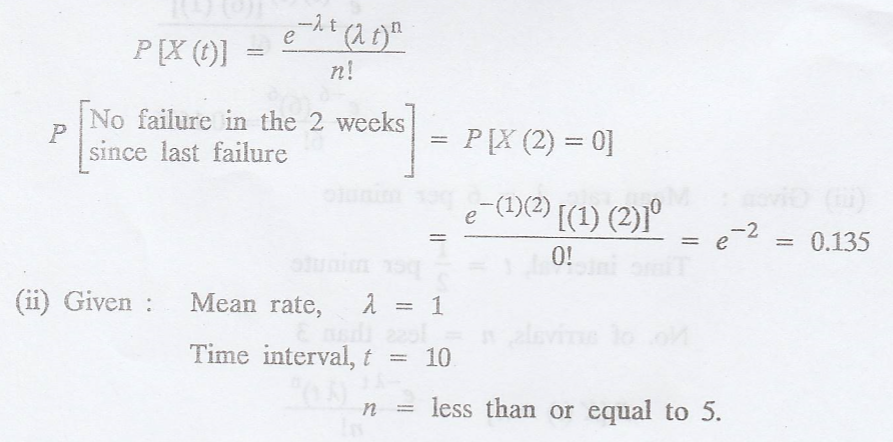
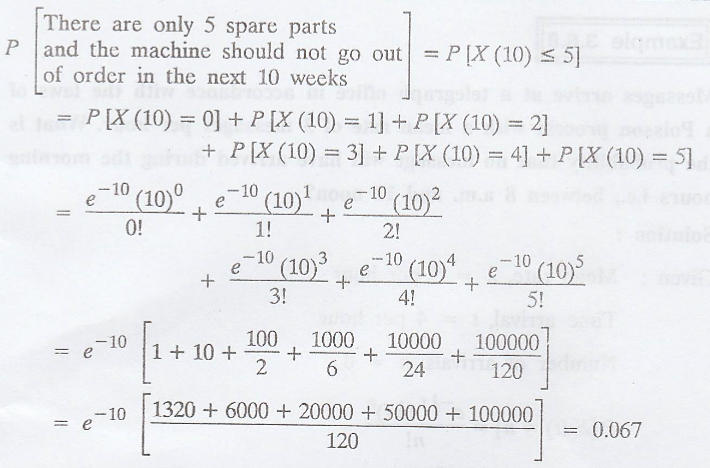
Example 3.6.7

Patients arrive randomly and independently at a doctor's consulting room from 8 a.m. at an average rate of one in 5 min. The waiting room can hold 12 persons. What is the probability that the room will be full when the doctor arrives at 9 a.m?

Solution :

Let X(t) be the number of patients arrive doctor's room in the time interval t.

Given: Mean rate, λ = 12 per hour

['.' 1 in 5 min ⇒ 12 in 60 min => 12 in 1 hour]

Time interval, t = 1 per hour

No. of arrivals, n = 12

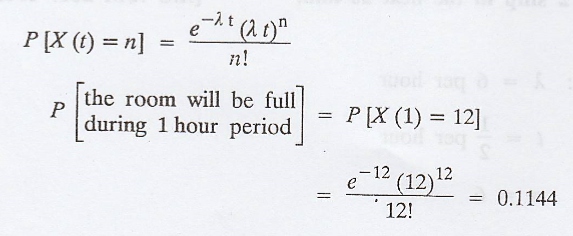
Example 3.6.8

Messages arrive at a telegraph office in accordance with the laws of a Poisson process with a mean rate of 3 messages per hour. What is the probability that no message will have arrived during the morning hours i.e., between 8 a.m. and 12 noon?

Solution :

Given: Mean rate, λ = 3 per hour

Time arrival, t = 4 per hour

Number of arrivals, n = 0

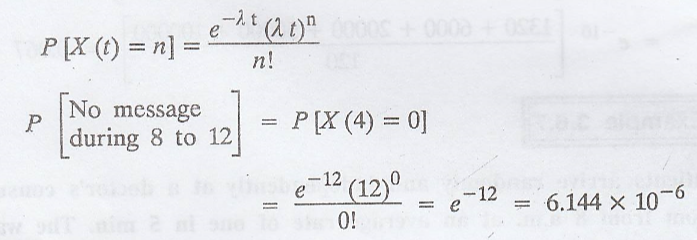
Example 3.6.9

On the average, a submarine on patrol sights 6 enemy ships per hour. Assuming that the number of ships sighted in a given length of time is a Poisson variate, find the probability of sighting

(i) 6 ships in the next half-an-hour.

(ii) 4 ships in the next 2h,

(iii) atleast 1 ship in the next 15 min.

(iv) atleast 2 ship in the next 20 min. [A.U A/M 2017 R-13]

Solution :

(i) Given: λ = 6 per hour

t = 1/2 per hour

n = 6

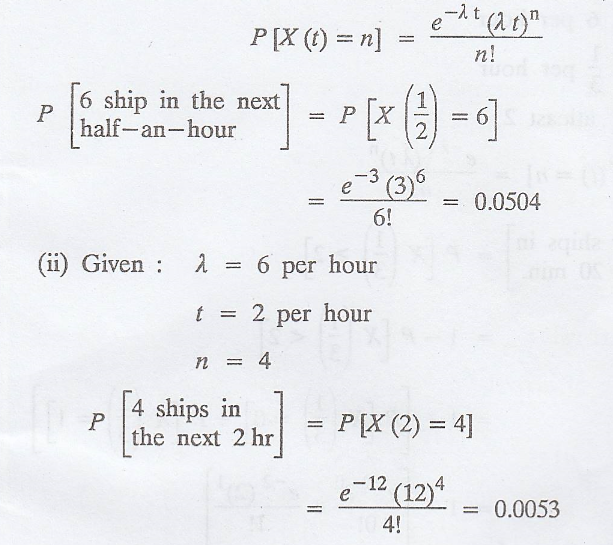
(iv) Given: λ = 6 per hour

t = 1/3 per hour

n = atleast 2

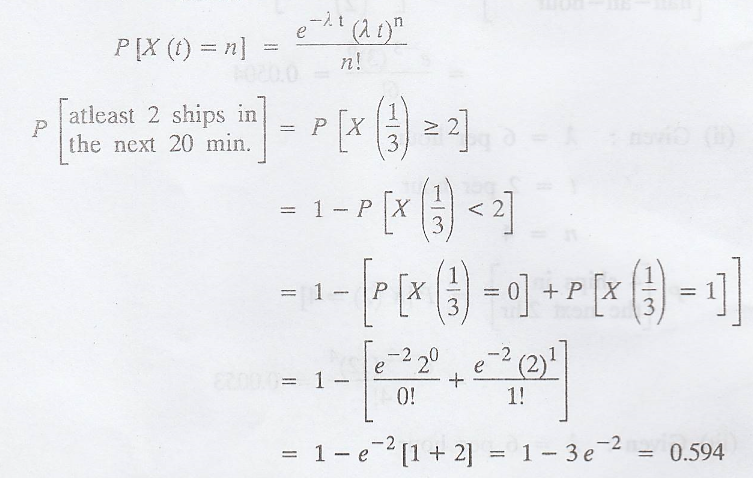
Example 3.6.10

VLSI chips, essential to the running of a computer system, fail in accordance with a Poisson distribution with the rate of one chip in about 5 weeks. If there are two spare chips on hand, and if a new supply will arrive in 8 weeks, what is the probability that during the next 8 weeks the system will be down for a week or more, owing to the lack of chips? [AU Nov. 2007]

Solution :

Given: Mean rate, λ = 1/5

Time interval, t = 7

Number of arrivals, n = greater than 2

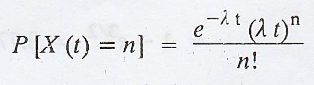
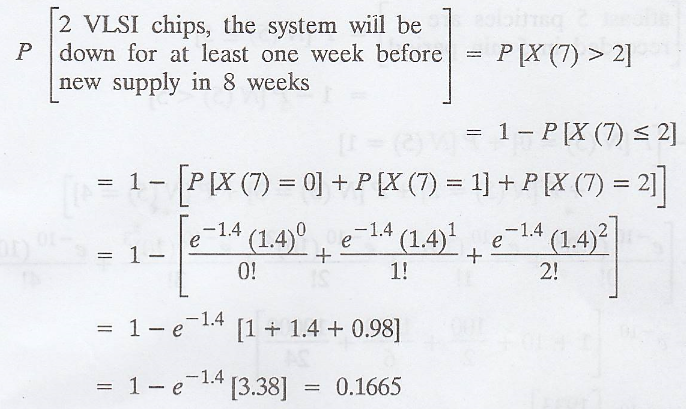
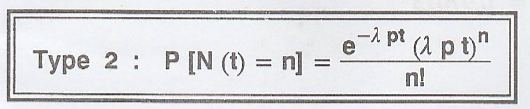
Example 3.6.11

A radio active source emits particles at the rate of 6 per minute in a Poisson process. Each emitted particle has a probability of 1/3 being recorded. Find the probability that atleast 5 particles are recorded in a 5 minute-period. [A.U N/D 2018 R13 RP]

Solution :

N(t) is a Poisson process with parameter λp

Mean rate, λ = 6 per minute

Event has a constant probability, p = 1/3

Time interval, t = 5 per minute

Number of recorded, n = 5

λpt = (6) (1/3) (5) = 10

P[N(t) = n] = e ^{– λ t} (λt) ⁿ / n!

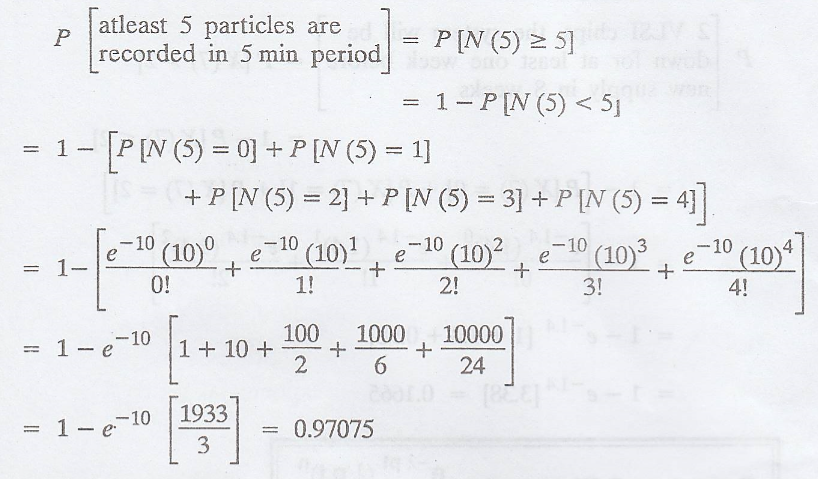
Example 3.6.12

A radioactive source emits particles at a rate of 5 per minute in accordance with Poisson process. Each particle emitted has a probability 0.6 of being recorded. Find the probability that 10 particles are recorded in 4-min period. [A.U N/D 2014] [A.U A/M 2019 R13 PQT]

Solution :

N(t) is a Poisson process with parameter λp

Mean rate, λ = 5 per minute ho

Event has a probability constant, p = 0.6

Time interval, t = 4 per minute

No. of recorded, n = 10

λpt = (5) (0.6) (4) = 12

P[N(t) = n] = e ^{– λ t} (λt) ⁿ / n!

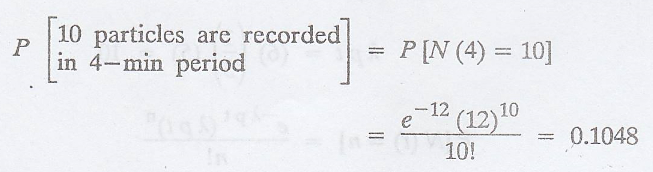
Type 3.

Example 3.6.13

If customers arrive at a counter in accordance with a Poisson process with a mean rate of 2 per minute, find the probability that the interval between 2 consecutive arrivals is (i) more than 1 min, (ii) between 1 min. and 2 min. and (iii) 4 min. or less. [A.U. 2006 N/D 2010, N/D 2011 M/J 2012]

Solution :

By the property of Poisson process, the interval T, between 2 consecutive arrivals follows an exponential distribution with parameter (λ = 2)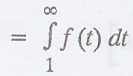 

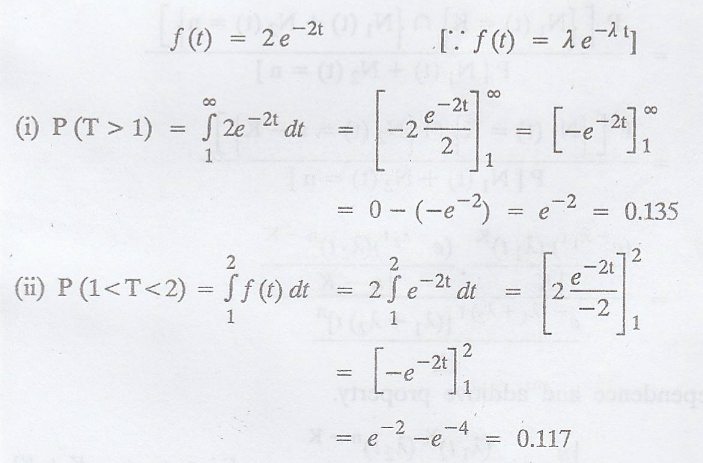
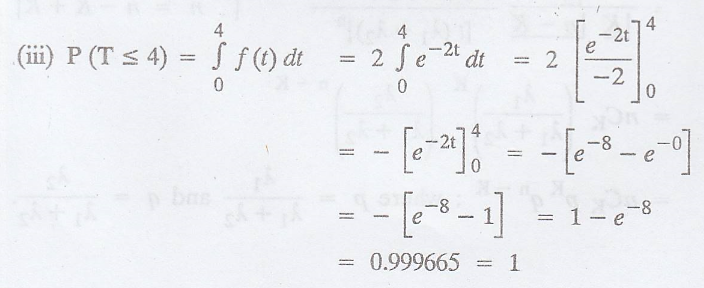
Example 3.6.14

If {N₁(t)} and {N₂(t)} are 2 independent Poisson process with parameters λ₁ and λ₂ respectively, Show that

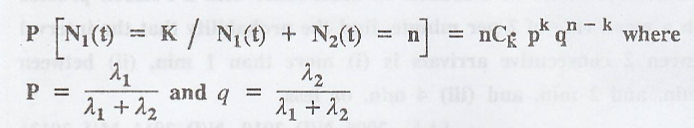
[A.U N/D 2015 R-8, A.U A/M 2018 R-8] [A.U A/M 2019 R17 RP]

Solution:

The required conditional probability is

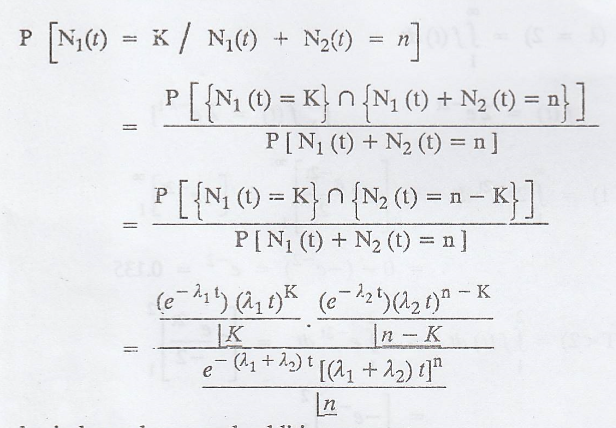
by independence and additive property.

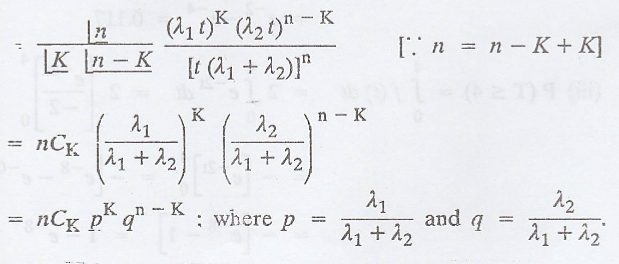
Example 3.6.15

If {X(t)} and {Y(t)} are two independent Poisson processes, show that the conditional distribution {X(t)} given {X(t) + Y(t)} is binomial. [A.U. N/D 2006]

Solution:

Let {X(t)} & {Y(t)} be two independent Poisson processes with λ₁t & λ₂t respectively. Hence {X(t) + Y(t)} is also Poisson process with parameter λ₁t + λ₂t

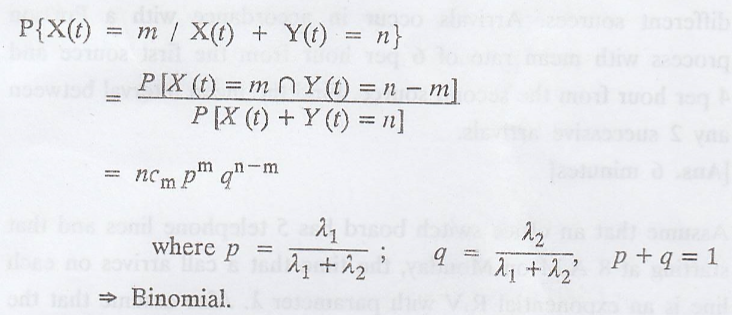
Example 3.6.16

Examine whether the Poisson process X(t) given by the probability law P[N(t) = n] = e ^{– λ t} (λt) ⁿ / n!, n = 0, 1, 2, ... is covariance stationary or not. [A.U A/M 2005, A.U. N/D 2007] [A.U A/M 2019 (R17) RP]

Solution:

Given: X(t) = P[N(t) = n] = e ^{– λ t} (λt) ⁿ / n!

We know that X(t) is a Poisson distribution with parameter λt.

→ E[X(t)] = λt ≠ a constant.

→ The Poisson process is not a SSS process and not a WSS process.

→ The Poisson process is not a covariance stationary.

EXERCISE 3.6

1. Assume that a circuit has a IC whose time to failure is an exponentially distributed R.V with expected life time of 3 months. If there are 10 spare IC's and time from failure to replacement is zero, what is the probability that the circuit can be kept operational for atleast 1 year? [Ans. 0.9972]

2. Suppose that customers arrive at a counter independently from 2 different sources. Arrivals occur in accordance with a Poisson process with mean rate of 6 per hour from the first source and 4 per hour from the second source. Find the mean interval between any 2 successive arrivals. [Ans. 6 minutes]

3. Assume that an office switch board has 5 telephone lines and that starting at 8 A.M on Monday, the time that a call arrives on each line is an exponential R.V with parameter λ. Also assume that the calls arrive independently on the lines. Show that the time of arrival of the first call (irrespective of which line it arrives on) is exponential with parameter 5λ.

4. Passengers arrive at a terminal for boarding the next bus. The times of their arrival are Poisson with an average arrival rate of 1 per minute. The times of departure of each bus are Poisson with an average departure rate of 2 per hour. Assume that the capacity of the bus is large. Find the average number of passengers in (i) each bus, (ii) the first bus leaves after 9 a.m. [Ans. 30, 60]

5. Students enter a hall at a Poisson rate of λ = 1 per second. What is the expected time until the eleventh student arrives? What is the probability that the elapsed time between the eighteenth and nineteenth student arrivals exceed two seconds ? [Ans. 11 sec, 0.13]

6. The number of typographical errors on a single page of a document is poisson distributed with λ = 1. What is the probability that there is atleast one error on a page ? [Ans. 0.633]

7. A hospital receives an average of 3 emergency calls in a 10 minute interval. What is the probability that there are atmost 3 emergency calls in 10 minutes interval. [Ans. 0.647]

8. A hard disk fails in a computer system and it follows a Poisson distribution with mean rate of 1 per week. Find the probability that 2 weeks have elapsed since last failure. If we have 5 extra hard disks and the next supply is not due in 10 weeks, find the probability that the machine will not be out of order in the next 10 weeks. [Ans. 0.135, 0.068] [AU June 2007] [A.U N/D 2017 (RP) R-13]

9. A fisherman catches fish at a Poisson rate of 2 per hour from a large pond with lots of fish. If he starts fishing at 10.00 a.m., What is the probability that he catches one fish by 10.30 a.m. and three fish by noon? [Ans. 0.082] [AU April 2004] [A.U A/M 2017 (RP) R-13]