Norm of a vector

(b) Norm of a vector || ||

Definition :

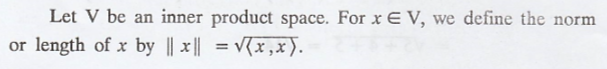
Example :

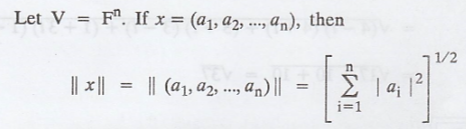
is the Euclidean definition of length.

Note: If n = 1, we have || a || = | a |

Definition: Let V be a vector space over F, where F is either R or C. Regardless of whether V is or is not an inner product space, we may still define a norm || . || as a real-valued function on V satisfying the following three axioms for all x, y Є V and a Є F.

Axiom 1 : || x || ≥ 0, and || x || = 0 if and only if x = 0

Axiom 2 : || ax || = a. | x ||

Axiom 3 : || x + y || ≤ | x || + || y ||

Problem 1.

Let x = (2,1 + i, i) and y = (2-i, 2, 1+2i) be vectors in C³. Compute || x |, || y || and || x + y ||

Solution :

Problem 2.

Solution :

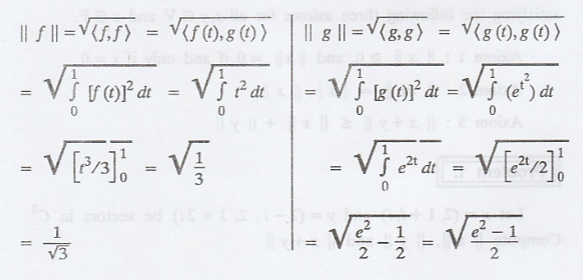
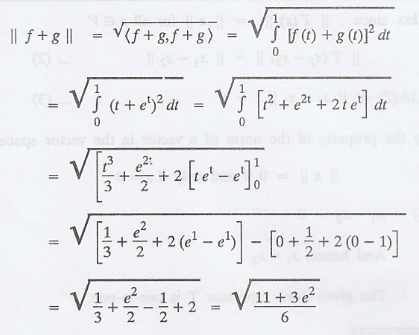
Problem 3.

Let T be a linear operator on an inner product space V, and suppose that || T(x) || = || x || for all x. Prove that T is one-to-one.

Solution :

Let V be a vector space and T be a linear operator on V.

Let || T (x) || = || x || for all x

To prove : T is one to one.

Proof :

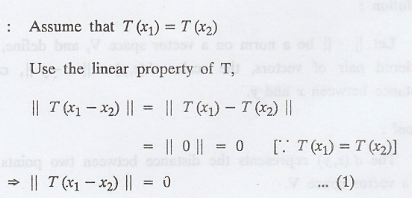
Also, since || T (x) || = ||x|| for all x Є V

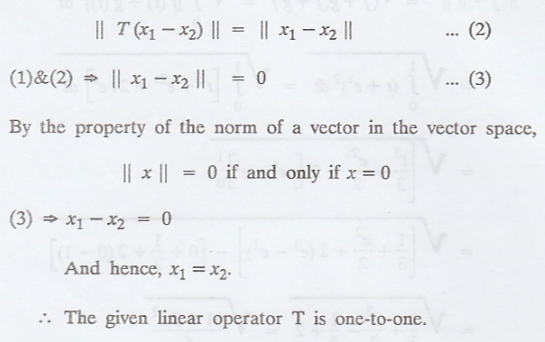
Problem 4.

Let ||'|| be a norm on a vector space V, and define, for each ordered pair of vectors, the scalar d (x, y) = || x - y ||, called the distance between x and y. Prove the following results for all x, y, z Є V.

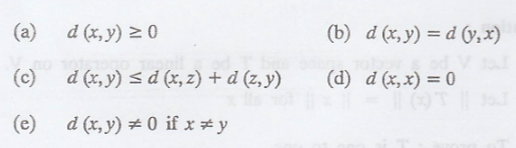
Solution :

Let ||'|| be a norm on a vector space V, and define, for each ordered pair of vectors, the scalar d (x, y) = ||x - y||, called the distance between x and y.

Proof :

The d (x,y) represents the distance between two points x and y cf a vector space V.

Distance is always taken as positive.