Moments - Moments Generating Functions and Their Properties

MOMENTS - MOMENT GENERATING FUNCTIONS AND THEIR PROPERTIES

Moments [Discrete case]

Let X be discrete R.V. taking the values x₁, x₂, ... x_n with probability mass function p₁, p₂, ... p_n respectively then the r^th moment about the origin is

In particular from (1)

Moments [Continuous case]

If X is a continuous R.V. with probability density function f(x) defined in the interval (a, b) then

Moments Generating Function (M.G.F)

An important device that can be used to calculate the higher moments is the moment generating function.

Moment generating function of a random variable X about the origin is defined as

where t being a real parameter assuming that the integration or summation is absolutely convergent for some positive number h such that |t| < h

.'. MX(t) generates moments about the origin and hence we call it as moment generating function.

Note

Limitations of m.q.f

1. A random variable X may have no moment although its m.g.f exists.

2. A random variable X can have its moment generating function and some (or all) moments, yet the moment generating function does not generate the moments.

3. A random variable X can have all or some moments, but moment generating function do not exist except perhaps at one point.

Properties of moment Generating function [A.U Tvli. A/M 2009]

Let Y = aX + b, where X is a R.V with moment generating function MX(t). Then

2.  where c is a constant.

3. If X and Y are two independent random variables, then

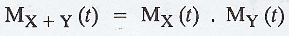
Proof : 

Example 1.6.1

Find the moment generating function of the RV X whose probability function P(X = x) = 1/2^x, x = 1,2,... Hence find its mean. [A.U Tvli A/M 2009] [A.U CBT A/M 2011] [A.U N/D 2018 PQT R-13]

Solution:

Example 1.6.2

If X represents the outcome, when a fair die is tossed, find the moment generating function (MGF) of X and hence find E(X) and Var(X). [A.U A/M 2018 R-13]

Solution:

The probability distribution of X is given by

Example 1.6.3

Find the probability distribution of the total number of heads obtained in four tosses of a balanced coin. Hence obtain the MGF of X, mean of X and variance of X. [AU A/M 2008]

Solution :

(i) MGF

Example 1.6.4

For a discrete random variable. X with probability function

Show that E(X) does not exist eventhough m.g.f exists. [A.U N/D 2012]

Solution:

Given: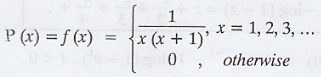 

Hence, E(X) does not exist.

Now, we have, by definition the m.g.f as

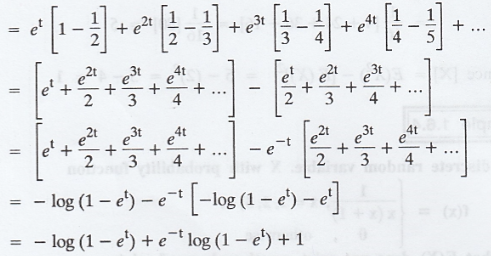
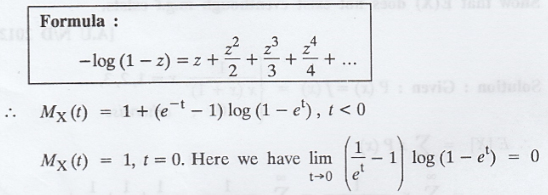
by using L'Hospital rule for indetermine form (0 x ∞) and M_x(t) does not exist for t > 0

Example 1.6.5

For the triangular distribution

find the mean, variance and the moment generating function (MGF) also find cdf of F(x). [A.U. M/J 2006, N/D 2013] [A.U CBT M/J 2010, CBT N/D 2011] [A.U N/D 2013] [A.U A/M 2018 R-08] [A.U N/D 2018 R13 RP]

Solution

Given: f(x) = 

Mean = 

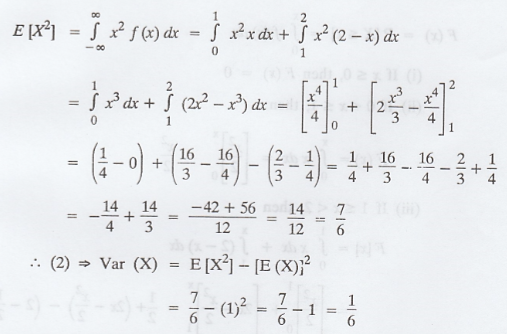
The moment generating function of the Random variable X is

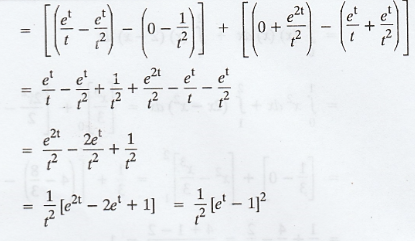
To find the cdf of F (x)

Example 1.6.6

Let the random variable X have the p.d.f

Find the moment generating function, mean and variance of X. [A.U. A/M. 2005, N/D 2012] [A.U A/M 2019 (R8) RP]

Solution:

The m.g.f is given by

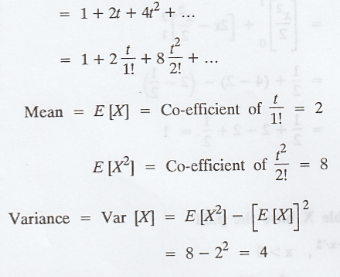
Example 1.6.7

The density function of a random variable x is given by

f(x) = Kx (2-x), 0 ≤ x ≤ 2. Find K, mean, variance and r^th moment. [A.U. N/D 2006] [A.U. M/J 2007] [A.U Trichy A/M 2010]

Solution :

Given: f (x) = Kx (2-x), 0 ≤ x ≤ 2 is a p.d.f.

We know that, if f (x) is a p.d.f then,

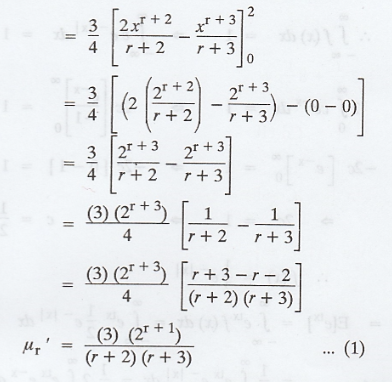
Example 1.6.8

A continuous R.V. X has the p.d.f f(x) given by f(x) = ce^-|x|, -∞ < x < ∞. Find the value of c and moment generating function of X. [A.U. M/J 2007]

Solution :

Given: f(x) = ce^-|x|

Given f(x) is a p.d.f.

Example 1.6.9

If a R.V X has the mgf  obtain the standard deviation of X [A.U A/M 2018 R-08]

Solution :

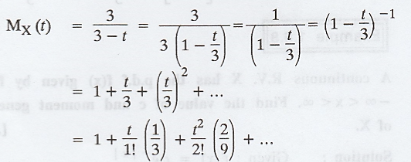
Example 1.6.10

The first four moments of a distribution about X = 4 are 1, 4, 10 and 45 respectively. Show that the mean is 5, variance is 3, µ₃ = 0 and µ₄ = 26. [A.U. N/D. 2004]

Solution:

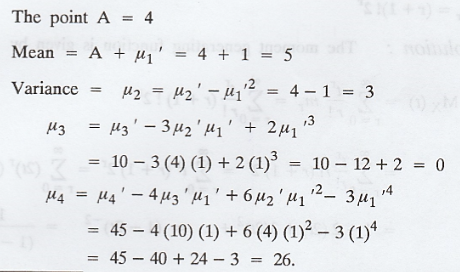
Example 1.6.11

If a RV X has the moment generating function M_X(t) = 2/2-t determine the variance of X. [A.U M/J 2012]

Solution :

Example 1.6.12

Find the moment generating function of the RV whose moments are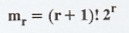 

Solution:

The moment generating function is given by

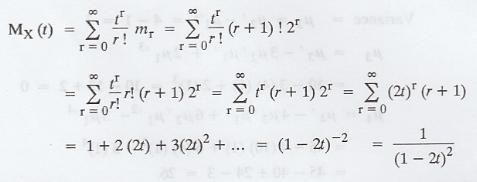
Example 1.6.13

A random variable X has density function given by

Find (1) m.g.f. (2) rth moment (3) mean (4) variance [AU N/D 2006]

Solution :

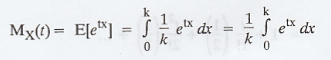
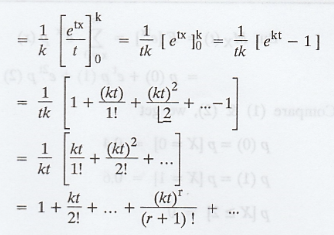
Example 1.6.14

If the moments of a random variable 'X' are defined by E (X^r) = 0.6; r = 1, 2, 3, ...

Show that P (X = 0) = 0.4, P (X = 1) = 0.6, P (X ≥ 2) = 0 [AU N/D 2008]

Solution:

We know that,

Example 1.6.15

Prove that the moment generating function of the sum of a number of independent random variables is equal to the product of their respective moment generating functions. [AU N/D 2006]

Solution:

Given:

Example 1.6.16

Let X be a R.V. with p.d.f f(x) = 

Find,

(1) P(X > 3)

(2) Moment generating function of X

(3) E(X) and Var(X) [AU M/J 2007]

Solution:

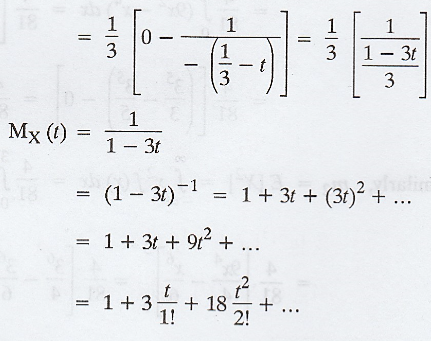
Example 1.6.17

Find the first four moments about the origin for a random variable X having the pdf.

[AU N/D 2008] [A.U N/D 2016 R13 PQT] [A.U N/D 2019 (R17) PS]

Solution:

Given: f(x) = 

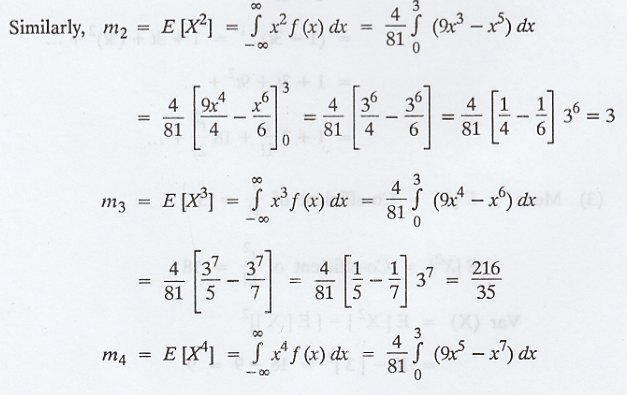
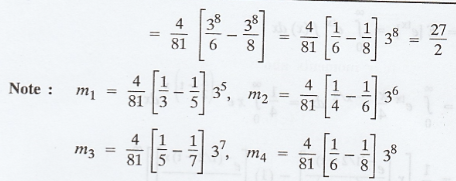
Example 1.6.18

Give an example to show that if pdf exists but MGF does not exist.

Solution:

Let f (x) =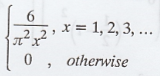 

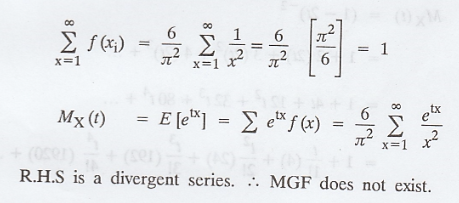
R.H.S is a divergent series. .'. MGF does not exist.

Example 1.6.19

Find the M.G.F. of the random variable X having the probability density function

Also deduce the first four moments about the origin. [A.U N/D 2010, M/J 2012] [A.U A/M 2017 R13]

Solution:

Given: f(x) = 

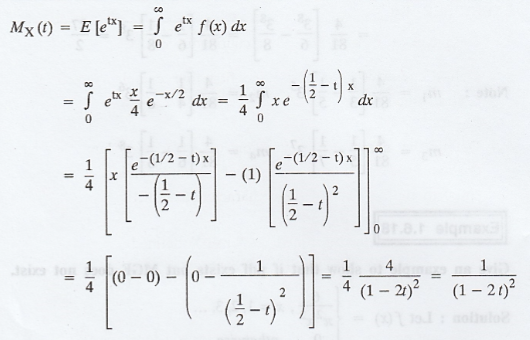
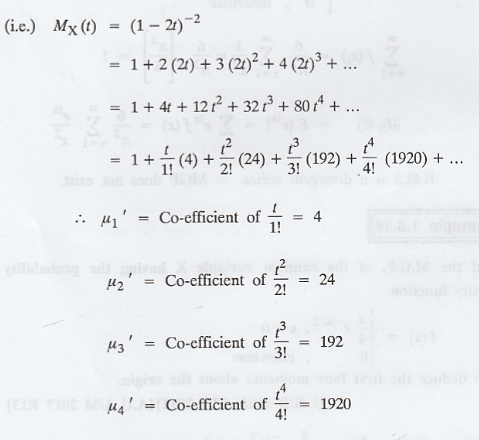
EXERCISES 1.6

1. Define m.g.f. of a discrete and continuous r.v. X.

2. Define cumulants and obtain the first four cumulants interms of central moments.

3. Define the characteristic function of a r.v. X. Show that the bas characteristic function of the sum of two independent variables is equal to the product of their characteristic function.

4. Find the characteristic function of r.v. X defined as 

5. State any two properties of the characteristic function of a r.v. X.

6. Find the characteristic function whose probability density function is  

7. Show that the rth moment for the distribution , c is positive and 0 ≤ x ≤ 8 is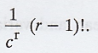 

8. Find the density function of the distribution for which the characteristic function is given by 

9. If the m.g.f of a R.V. 'X' is 2/(2-t), then find the S.D of X. [Ans.1/2]

10. Find the m.g.f of a r.v. X whose density function is given by . Hence find its mean and variance.

11. The random variable X assumes the value x with the probability P(X=x) = q^1-xp, x = 1, 2, 3, ... Find the m.g.f of X and find its mean and variance. 

12. Find the m.g.f for the given distribution 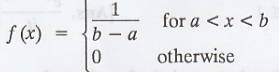 Also, find µ₁' and µ₂' by two different methods.

13. A random variable X has the p.d.f.  Find its m.g.f mean and variance. [Ans. 

14. Give the significance of moments of a random variable.

15. Define n^th moment about origin for a random variable.

16. Find the moment generating function of a R.V X having the density function f (x) =  Using the generating function, find the first four moments about the origin.