Matrix Vector

(c) Matrix Vector

Problem 1.

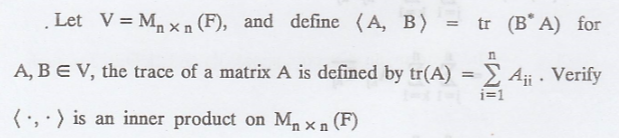
Solution:

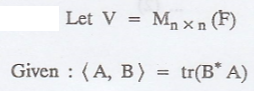
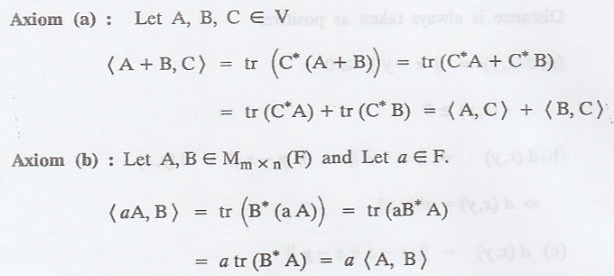
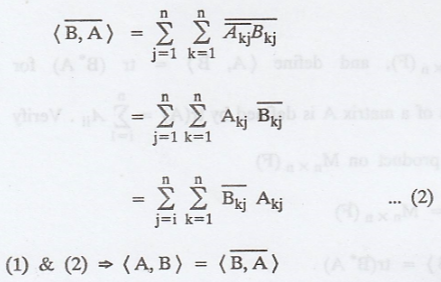
Thus, all the axioms are satisfied.

Hence the proof.

Problem 2.

Use the Frobenius inner product to compute || A ||, || B ||, and <A, B> for

Solution:

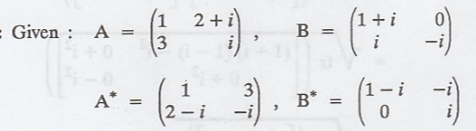
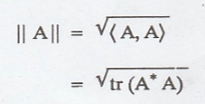
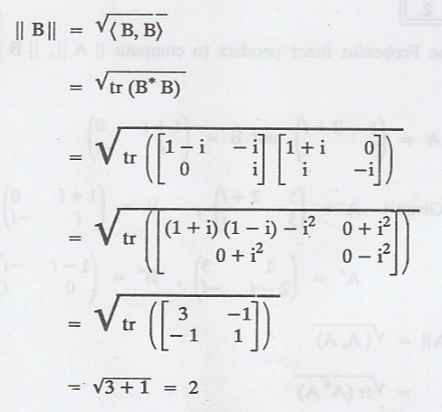
Problem 3.

Let A and B be n x n matrices, and let c be a scalar. Prove that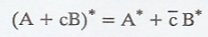 

Solution :

Let A and B be n x n matrices and c be a scalar.

The conjugate transpose of n x n matrix A is n xn matrix A* such that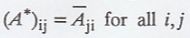 

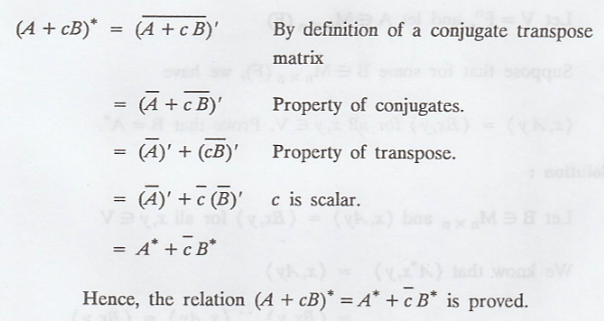
Problem 4.

Solution :

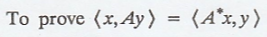
By the definition of the standard inner product

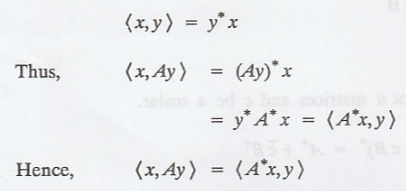
Problem 5

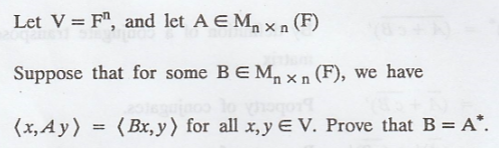
Solution :

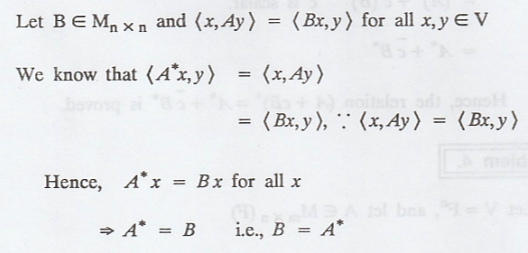
Problem 6.

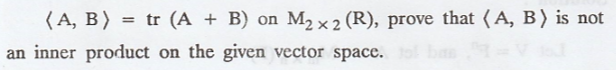
Solution :

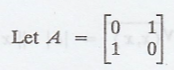
The inner product <A, A> is given by,

Here, <A, B> = 0 which is a contradiction to axiom (d) of inner product.

Therefore, <A, B> = tr (A + B) is not an inner product on M_2x2(R)