Linear Transformation

LINEAR TRANSFORMATION, NULL SPACES,  AND RANGES                                                         

Definition :

Let V and W be vector spaces (over F). We call a function T : V → W a linear transformation from V to W if, for all x, y, Є V and c Є F, we have

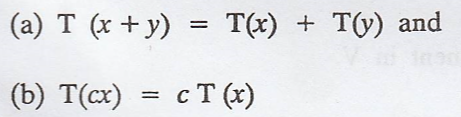
Properties of T is linear

Properties of a function T : V → W.

1. If T is linear, then T(0) = 0.

2. T is linear if and only if T (cx + y) = cT(x) + T(y) for all x, y Є V and c Є F.

3. If T is linear, then T (x - y) = T(x) - T(y) for all x, y Є V.

4. T is linear if and only if, for x₁, x₂, ..., x_n Є V and a₁, a₂, ..., a_n Є F, we have

Note: We generally use property 2 to prove that a given transformation is linear.

Property 1:

If T is a linear, then T(0) = 0

Proof:

Given: T is linear.

where x is an arbitrary element in V.

Property 2.

T is linear if and only if T(cx + y) = c T(x) + T(y) for all x,y Є V and c Є F.

Proof:

Given: T is linear

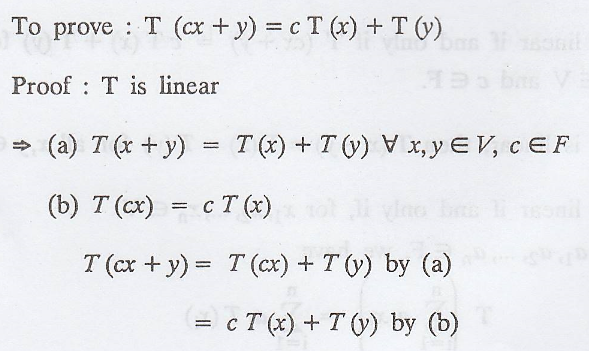
Converse part :

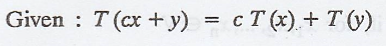
To prove T is linear.

Since 0 vector is in the vector space V,

we replace y with the 0 vector.

Property 3.

If T is linear, then T(x - y) = T(x) - T(y) for all x, y Є V.

Proof :

Given : T is a linear transformation.

To prove :

T(ax + by) = aT(x) + bT(y) for any scalars a,b Є F and vectors x,y Є V

Since 1 and -1 are scalars, we use a = 1, b = -1 in the above equation to give

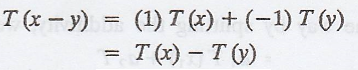
Property 4.

T is linear if and only if, for x₁, x₂,..., x_n Є V and a₁, a₂, ..., a_n Є F, we have

Proof:

Given: T is a linear transformation.

To prove that

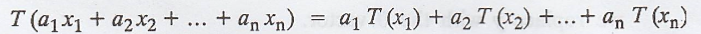
We know that, linear combination of vectors in V is also a vector in V.

Continuing in the same way by splitting the additivity, we get

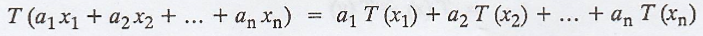
Converse part :

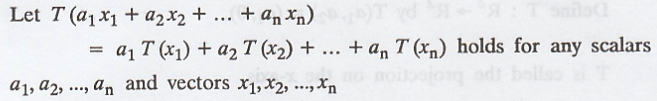
Since 0 vector is in V, we replace a₃ = a₄ = ... = a_n = 0 and a₁ = a₂ = 1, then we are left with

In other words, 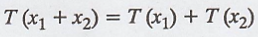 which satisfies the first part of the definition.

Similarly, Put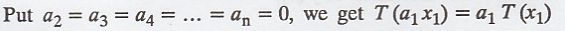 

This proves the second part of the definition.

Thus, T is a linear transformation.

Example 1.

For any angle θ, define  by the rule :

T_θ(a₁, a₂) is the vector obtained by rotating (a₁, a₂) counterclockwise by θ if (a₁, a₂) ≠ (0, 0), and T_θ(0, 0) = (0, 0).

Then 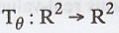 is a linear transformation that is called the rotation by θ.

Example 2.

Define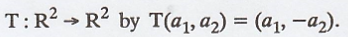 

T is called the reflection about the x-axis.

Example 3.

Define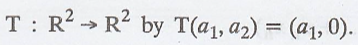 

T is called the projection on the x-axis.

Example 4.

Define 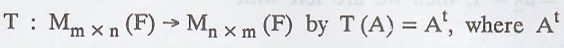 is the transpose of A. Then T is a linear transformation.

Example 5.

Define 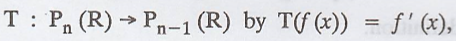 where ƒ'(x) denotes the derivative of f(x).

To show that T is linear, let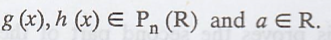 

Now

So by property 2, T is linear.

Example 6.

Let V = C(R), the vector space of continuous real-valued functions on R. Let a, b Є R, a < b.

Define 

Then T is a linear transformation.