Linear Dependence and Linear Independence

LINEAR DEPENDENCE AND LINEAR INDEPENDENCE

Definition :

A sub-set S of a vector space V is called linearly dependent if there exist a finite number of distinct vectors u₁, u₂, ..., u_n in S and scalars a₁, a₂, ... a_n, not all zero, such that

Note: In this case we also say that the vectors of S are linearly dependent.

For any vectors u₁, u₂, ..., u_n, we have

We call this the trival representation of 0 as a linear combination of u₁, u₂, ..., u_n. Thus, for a set to be linearly dependent, there must exist a non-trivial representation of 0 as a linear combination of vectors in the set.

Consequently, any subset of a vector space that contains the zero vector is linearly dependent, because 0 = 1.0 is non-trivial representation of 0 as a linear combination of vectors in the set.

Definition :

A subset S of a vector space that is not linearly dependent is called linearly independent. As before, we also say that the vectors of S are linearly independent.

The following facts are true in any vector space.

1. The empty set is linearly independent, for linearly dependent sets must be non-empty.

2. A set consisting of a single non-zero vector is linearly independent. For if {u} is linearly dependent, then au = 0 for some non-zero scalar a. Thus,

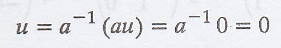
3. A set is linearly independent if and only if the only representations of 0 as linear combinations of its vectors are trival representations.

(a) Vector Space M = M_{m x n}

Problem 1.

Determine whether the following sets are linearly dependent or linearly independent.

Solution :

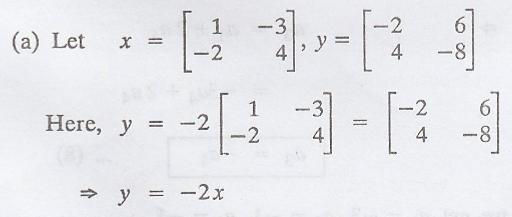
Hence, x,y are linearly dependent.

Put a₄ = 1, we get a₁ = -3, a₂ = -1, a₃ = −1

the values satisfy all the (1), (2), (3) & (4) equations.

Hence, u₁, u₂, u₃, u₄ are linearly dependent.

Problem 2.

In M_{2 x 3} (F), prove that the set

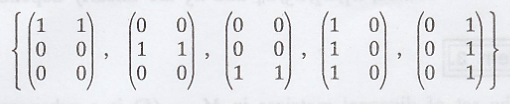
is linearly dependent.

Solution :

 

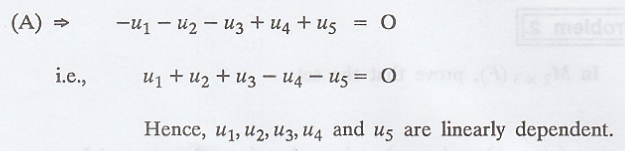
Problem 3.

The set of diagonal matrices in M_{2 x 2}(F) is a subspace. Find a linearly independent set that generates this sub-space.

Solution :

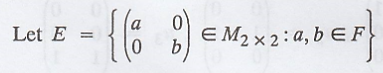
To prove that the linearly independent set that generates E.

First find the set that generates E.

The vector u can be written as,

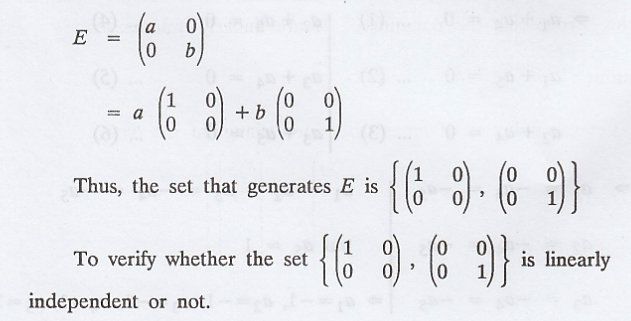
Hence, the linearly independent set that generates the subspace E is 

Problem 4.

Let M be a square upper triangular matrix with non-zero diagonal entries. Prove that the columns of M are linearly independent.

Solution :

Let the columns of an n x n upper triangular matrix

(b) Vector space - Linear dependence in R³ & R⁴, P_n(F)

Problem 1.

Let S = {(1, 3, -4, 2), (2, 2, -4, 0), (1, -3, 2, -4), (-1, 0, 1, 0)} in R⁴. We show that S is linearly dependent and then express one of the vectors in S as a linear combination of the other vectors in S.

Solution :

To show that S is linearly independent, we must find scalars a₁, a₂, a₃, and a₄, not all zero such that

One such solution is a₁ = 4, a₂ = −3, a₃ = 2, a₄ = 0. Thus S is a linearly dependent subset of R⁴, and

4 (1, 3, 4, 2) - 3 (2, 2, −4, 0) + 2 (1, −3, 2, −4) + 0 (−1, 0, 1, 0) = 0

Problem 2.

Determine the following sets are linearly dependent or linearly independent.

Solution :

Solving (1), (2) and (3) by using your calculator f_x991Ms

we get a₁ = a₂ = a₃ = 0

Hence, the s is linearly independent.

Put a₄ = 1, a₁ = 4, a₂ = 3, a₃ = -3

The values satisfied all the (5) equations.

.'. Hence, the set is linearly dependent.

Problem 3.

Show that the set {1, x, x²,...,xⁿ} is linearly independent in P_n(F)

Solution :

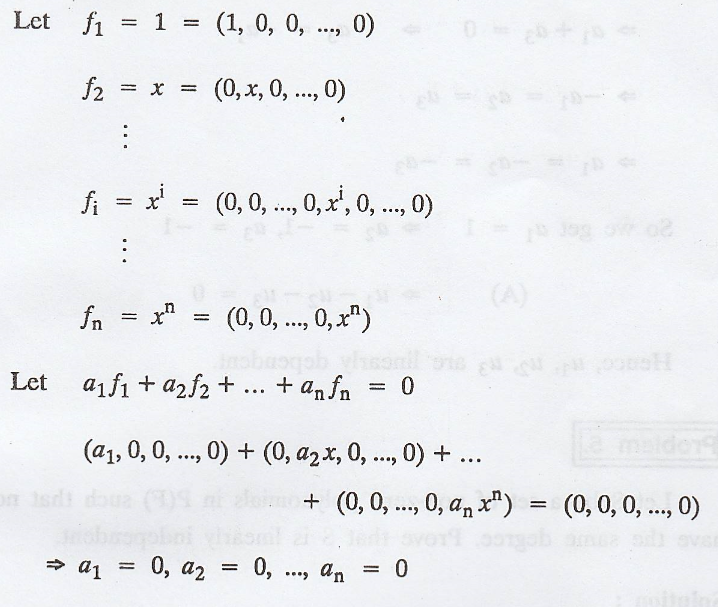
Thus, f₁,f₂, .... f_n are linearly independent.

i.c., S = {1, x, x², ...,.xⁿ) is linearly independent.

Problem 4.

Give an example of three linearly dependent vectors in R³ such that none of the three is a multiple of another.

Solution:

Given: None of the three is multiple of another

Problem 5

Let S be a set of non-zero polynomials in P(F) such that no two have the same degree. Prove that S is linearly independent.

Solution :

Given : S is the set of all non-zero polynomials.

By the definition of degree of polynomial a_nn ≠ 0

So these polynomials are linearly independent.

(c) Sub-set, span, finite set, F(R, R)

Theorem :

Let V be a vector space, and let  If S₁ is linearly dependent, then S₂ is linearly dependent.

Proof:

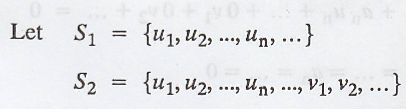
Given: S₁ is linearly dependent.

Then we have a₁, a₂, ..., a_n not all zero

Such that a₁u₁ + a₂u₂ + ... + a_n u_n + ... = 0

We can extend

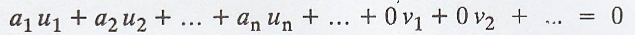
Clearly, this is the linear combination of vectors of S₂ such that not all a₁, a₂, …, a_n, … are zero.

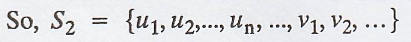
Satisfies the definition of linear dependence.

So, S₂ is linearly dependent.

Corollary :

Let V be a vector space, and  If S₂ is linearly independent, then S₁ is linearly independent.

Proof :

Given: S₂ is linearly independent.

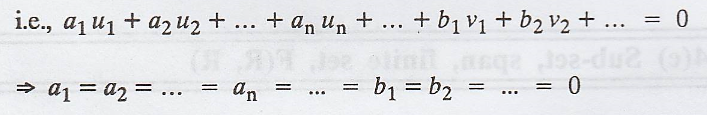
Conveniently, we write

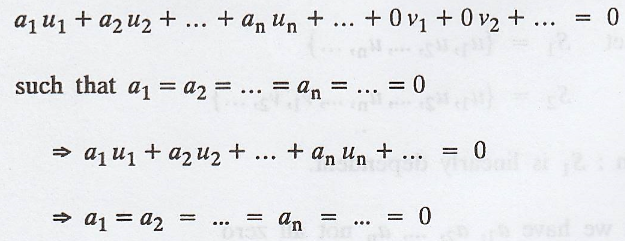
thus, u₁, u₂, ..., u_n are linearly independent

=> S₁ is linearly independent.

Theorem :

Let S be a linearly independent subset of a vector space V, and v be a vector in V that is not in S. Then S U {v} is linearly dependent if and only if v ε span(S)

Proof :

If S U {v} is linearly dependent, then u₁, u₂, ..., u_n ε S U {v}

such that for some non-zero scalars a₁, a₂, ..., a_n.

Since v ≠ v_i for i 1, 2, m, the coefficient of v in this linear combination is non-zero, and so the set {v₁, v₂, ..., v_m, v} is linearly dependent.

Therefore S U {v} is linearly dependent.

Problem 1.

Let S = {u₁, u₂, ..., u_n} be a linearly independent sub-set of a vector space V over the field Z2. How many vectors are there in span(S)? Justify your answer.

Solution :

Let V be a vector space and let S = {v₁, v₂, ..., v_n} be a subset of V then span (S) is the e set of all those vectors in V.

Let the linearly independent subset S = {u₁, u₂, ..., u_n} of a vector space V over the field Z₂.

Assume S has the maximum number of linearly independent vectors possible in V, and then clearly each of the vectors u_i, 1 ≤ i ≤ n is an n-tuple or in other words,

Since Z₂ = {0, 1}, then each place a_i have only two choices either 0 or 1 and there are total n places to fill.

Therefore, there are 2 x 2 x ... x 2 = 2ⁿ choices

Thus, the span(S) has 2ⁿ vectors.

Problem 2.

Let V be a vector space over a field of characteristic not equal to two. Let u, v and w be distinct vectors V.

Prove that {u, v, w} is linearly independent if and only if {u + v, v + w, u + w} is linearly independent.

Solution :

Given that u, v and w are distinct vectors in a vector space over the field of characteristic not 0.

Suppose {u, v, w} is a linearly independent set.

To prove : {u + v, v + w, u + w} is a linearly independent.

Let a(u + v) + b(v + w) + c(u + w) = 0 for some scalar a, b, c

=> (a + c) u + (b + a) v + (b + c) w = 0

Since {u, v, w} is linearly independent, the corresponding, scalars must be zero.

i.e., a + c = 0, b + c = 0, a + b = 0

Solving, we get a = b = c = 0

So, we have shown that whenever

a (u + v) + b (v + w) + c (u + w) = 0, we get

a = b = c = 0

=> {u + v, v + w, u + w} is a linearly independent set.

Converse Part:

Suppose {u + v, v + w, u + w} is a linearly independent set.

To prove {u, v, w} is a linearly independent set.

For, suppose p + q, q + r, r + p are any three scalars such that

(p + q) u + (q + r) v + (r + p) w = 0

=> p (u + w) + q (u + v) + r (v + w) = 0

Since {u + v, v + w, u + w} is linearly independent, the corresponding scalars must be zero.

i.e., p = q = r = 0

Consequently, p + q = 0, q + r = 0, r + p = 0

So, we have shown that whenever

(p + q) u + (q + r) v + (r + p) w = 0,

we get p + q = 0, q + r = 0, r + p = 0

⇒ {u, v, w} is linearly independent.

Hence, the proof.

EXERCISE 4.4

1. Determine whether the following sets are linearly dependent or linearly independent.

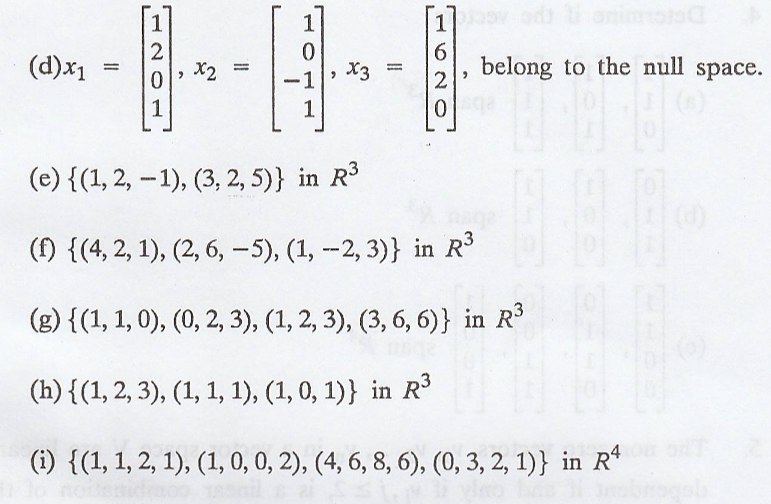
2. For what values of c are the vectors (-1, 0, -1), (2, 1, 2) and (1, 1, c) in R³ linearly dependent?

3. For what values of λ are the vectors t + 3 and 2t + λ² + 2 in P₁ linearly dependent?

4. Determine if the vectors

5. The non-zero vectors, v₁, v₂, ..., v_n in a vector space V are linearly dependent if and only if v_j, j ≥ 2, is a linear combination of the preceeding vectors v₁, v₂, v_j-1

6. Prove that if two vectors are linearly dependent, one of them is a scalar multiple of the other.

7. Under what conditions on the scalar 'a' are the vectors (a, 1, 0), (1, a, 1) and (0, 1, a) in R³ linearly dependent.

8. Show that the vectors u + v, u - v, u - 2v + w are linearly independent provided u, v, w are linearly independent.