Random Process and Linear Algebra: Unit IV: Vector Spaces,,
Linear Combinations and Systems of Linear Equations
Let V be a vector space and Let S a non-empty sub-set of V. A vector v ε V is called a linear combination of vectors of S if there exist a finite number of vectors
LINEAR
COMBINATIONS AND SYSTEMS OF LINEAR EQUATIONS
Definition
:
Let V be a vector space and Let S a non-empty sub-set of V.
A vector v ε V is
called a linear combination of vectors of S if there exist a finite number of
vectors

Note:
(1) If v = a1
u1+ a2 u2+ ... + an un
then v is a linear combination of u1, u2, ..., un
and a1, a2, ..., an are called co-efficients
of the linear combination.
(2) In any vector space
V, 0 v = 0 each v ε V
Thus the zero vector is
a linear combination of any non-empty sub-set of V.
(a) Solve
Linear equations :
Problem 1.

Solution
:
Rearrange the equations
['.' The first non-zero
coefficient of (1) must be one]
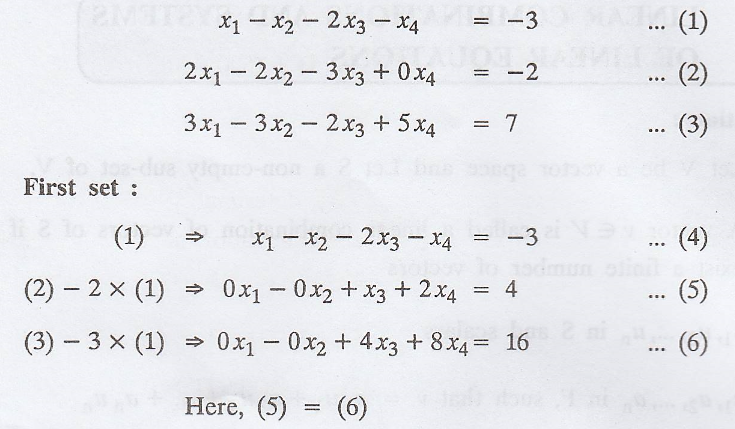


This can also be
expressed as

Problem 2.
For each list of
polynomials in P3(R), determine whether the first polynomial can be
expressed as a linear combination of the other two.
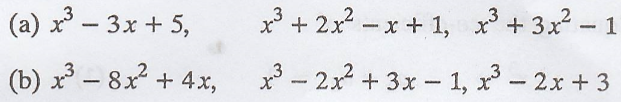
[A.U N/D 2019, R-17]
Solution
:

Equating the
coefficients of
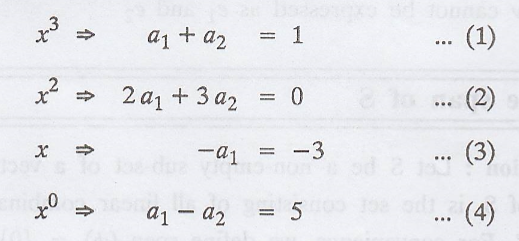
Solving (3) & (4),
we get, a1 = 3, a2 = -2
a1 = 3, a2
= -2 satisfying equations (1) & (2)

Hence, the result.
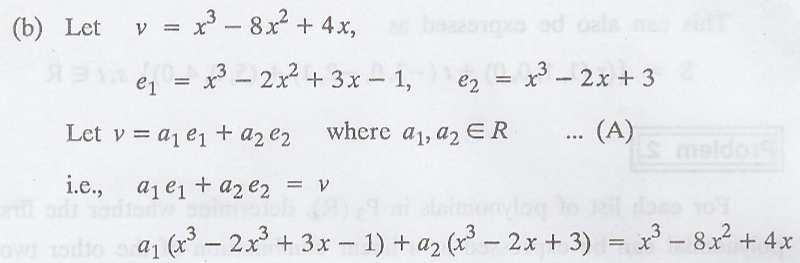
Equating the
co-efficients of


(b) The
span of S
Definition:
Let S be a non-empty sub-set of a vector space V. The span of S, is the set
consisting of all linear combinations of the vectors in S. For convenience, we
define span (φ) = {0}
Definition:
A sub-set S of a vector space V generates (or spans) V if span (S) = V.
Note: In this case, we also say that the vectors of S generate (or span) V.
Theorem 1.
The span of any sub-set S of a vector space V is a sub-space of V. Moreover,
any sub-space of V that contains S must also contain the span of S.
(or) The linear span
L(S) of any sub-set of a vector space V(F) is a sub-space of V(F). Moreover, 
Solution
:
(i) If S = φ because
span (φ) = {0} which is a sub-space that is connected in any sub-space of V.

Then there exist
vectors
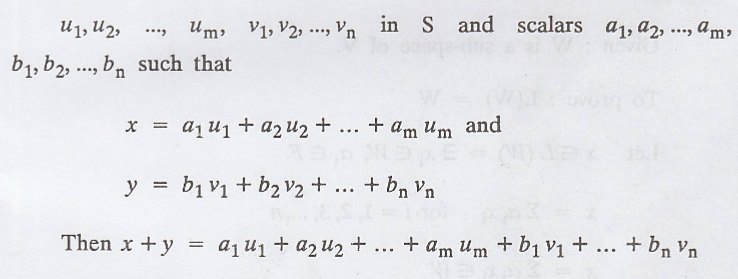
and, for any scalar c,
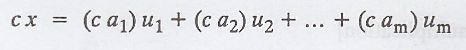
are clearly linear
combinations of the vectors in S.
So x + y and cx are in
span (S).
Thus span (S) is a
sub-space of V.
(ii) Let W denote any
sub-space of V that contains S.
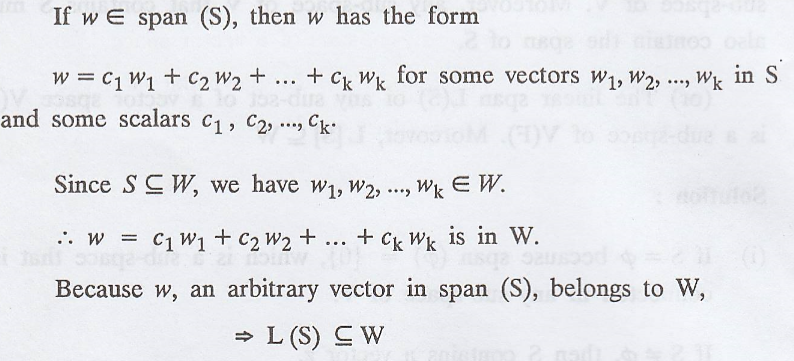
Problem 1.
Show that a sub-set W
of a vector space V is a sub-space of V if and only if span (W) = W.
Solution
:
Given: W is a sub-space
of V.

['.' W is a sub-space
of V, hence it is closed for addition and scalar multiplication]

Problem 2.

Solution
:

Problem 3.
In each part, determine
whether the given vector is in the span of S.
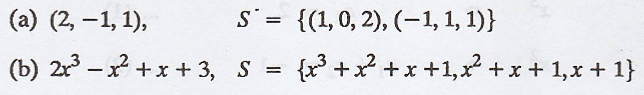
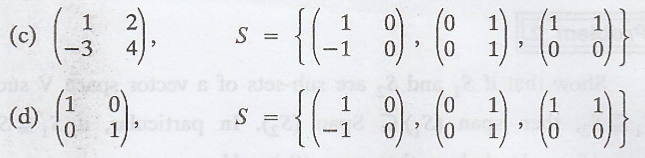
Solution
:
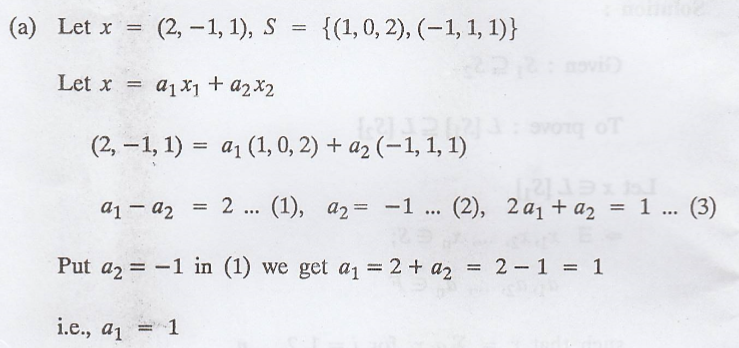

The given vector is in
the span of S.

Equating the coefficients of

.'. the given vector is
not the span of S.

.'. The given vector is
in the span of S.

.'. The given vector is
not in the span of S.
EXERCISE 4.3
1. Solve the following
systems of linear equations by the method introduced in this section.
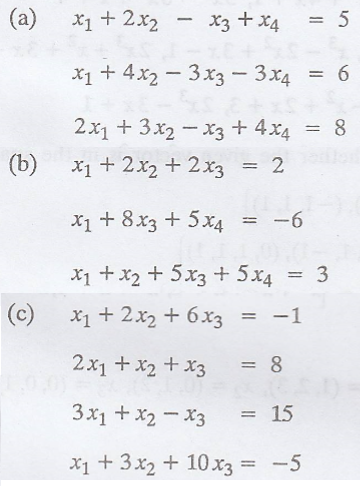
2. For each of the
following lists of vectors in R3, determine whether the first vector
can be expressed as a linear combination of the other two.
(a) (1, 2, -3), (-3, 2,
1), (2, -1, -1)
(b) (2, -1, 0), (1, 2,
-3), (1, -3, 2)
(c) (5, 1, −5), (1, -2,
-3), (-2, 3, -4)
(d) (-2, 2, 2), (1, 2,
-1), (-3, -3, 3)
3. For each list of
polynomials in P3(R), determine whether the first polynomial can be
expressed as a linear combination of the other two.

4. In each part,
determine whether the given vector is in the span S.
(a) (−1, 2, 1), S =
{(1, 0, 2), (−1, 1, 1)}
(b)(−1, 1, 1, 2), S =
{(1, 0, 1, −1), (0, 1, 1, 1)}
(c) (2, −1, 1, −3), S =
{(1, 0, 1, −1), (0, 1, 1, 1)}
(d) 
5. Show that the
vectors x1 = (1, 2, 3), x2 = (0, 1, 2), x3 =
(0, 0, 1) generate V3 (R)
6. Write the polynomial
V = t2 + 4t - 3 over R as a linear combination of polynomials e1
= t2 - 2t + 5, e2 = 2t2 - 3t, e3 =
t + 3
7. Write the vector x =  in vector space of 2 x 2 matrices as a linear combination of
in vector space of 2 x 2 matrices as a linear combination of 

8. Write the vector  in vector space of 2 x 2 matrices as a linear combination of
in vector space of 2 x 2 matrices as a linear combination of

9. If S and T are any
sub-sets of a vector space V(F), then
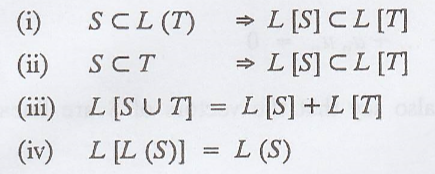
10. Show that (1, 1,
1), (0, 1, 1) and (0, 1, -1) generate R3.
11. Write the matrix  as a linear combination of
as a linear combination of

12. Solve :
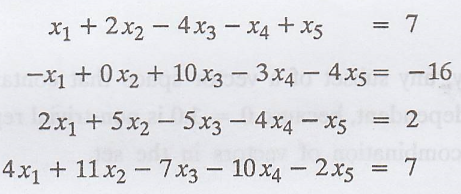
Random Process and Linear Algebra: Unit IV: Vector Spaces,, : Tag: : - Linear Combinations and Systems of Linear Equations
Related Topics
Related Subjects
Random Process and Linear Algebra
MA3355 - M3 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
