Laplace Transform Analysis of CT System

3.7 LAPLACE TRANSFORM ANALYSIS OF CT SYSTEM

Solution of differential equation:

The unilateral Laplace transforms used to solve differential equation with initial conditions.

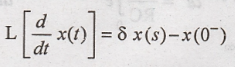
Laplace transform for network analysis, Laplace transform is mainly used to analyze the network effectively. Electrical components such as resistor, capacitor and inductors are represented by means of Laplace transform.

Laplace Transform of a Capacitor,

Voltage drop across the resistance is given by,

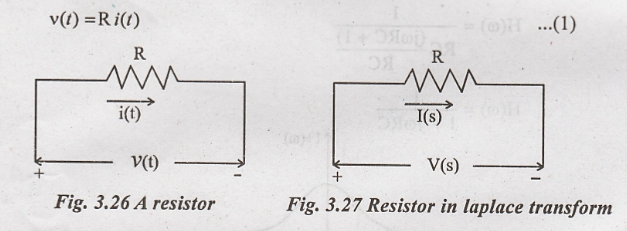
Laplace transform of (1) can be written as,

V(s) = RI(s)

Laplace transform of a single inductor

Voltage across the inductor is given as,

Taking Laplace transform of above equation.

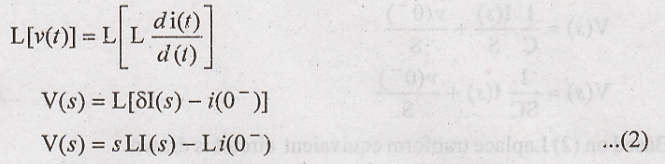
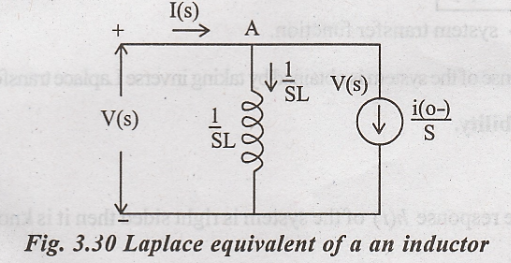
From equation (2) we have the current I(t) as

Based on (3) a new equivalent circuit can be drawn as follows.

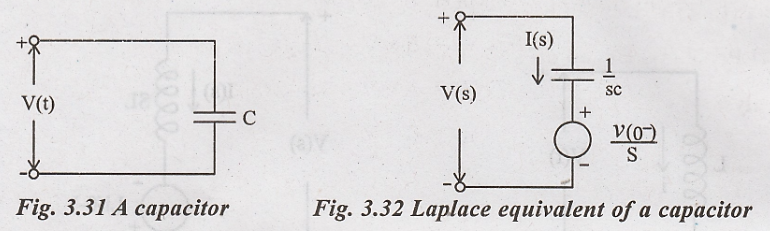
Laplace transform of a single capacitor

Voltage across a capacitor is given as

Taking Laplace transform of (1)

Based on (2) Laplace transform equivalent circuit is drawn.

Transfer function of a system.

Output of the LTI-CT system is given as

y(t) = h(t) * x(t)

Taking Laplace transform of above equation,

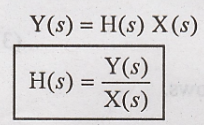
Here H(s) ⇒ system transfer function.

Impulse response of the system is obtained by taking inverse Laplace transform, of H(s).

Causality and stability.

Causality:

If the impulse response h(t) of the system is right sided then it is known as causal system.

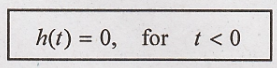
A Linear time invariant system (LTI) is said to be causal if all the poles of its system function lie on left side of the ROC.

Stability:

A system is said to be stable, if its impulse response is absolutely integral. i.e.,

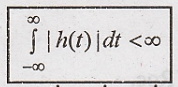
A linear time invariant system (LTI) system is said to be stable if ROC of its system function includes Re(s) = 0, i.e., jω axis of a plane,