Signals and Systems: Unit IV: Analysis of Discrete Time Signals,,
Inverse Z Transform
Inverse z Transform using Power Series Expansion, Inverse z-transform using partial fraction expansion
Inverse z transform can be obtained by (i) Power series expansion (ii) Partial fraction expansion (iii) Contour integration
INVERSE Z TRANSFORM
Inverse
z transform can be obtained by
(i)
Power series expansion
(ii)
Partial fraction expansion
(iii)
Contour integration
Inverse z Transform using Power Series Expansion
In
inverse x transform x(n) is obtained from X(z). From X(z), x(n) can be obtained
as
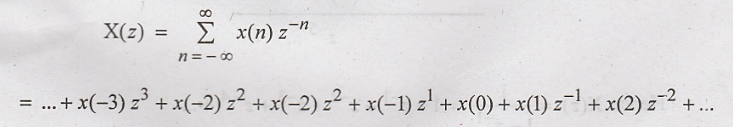
From
above expansion, the sequence x(n) can be obtained as
x(n)
= {..., x(-3), x(-2), x(-1), x(0), x(1), x(2), x(3)...}
Power
series expansion can be obtained directly (or) by long division method.
Problem 1:
Determine
inverse z transform of X(z) = 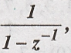
Solution:
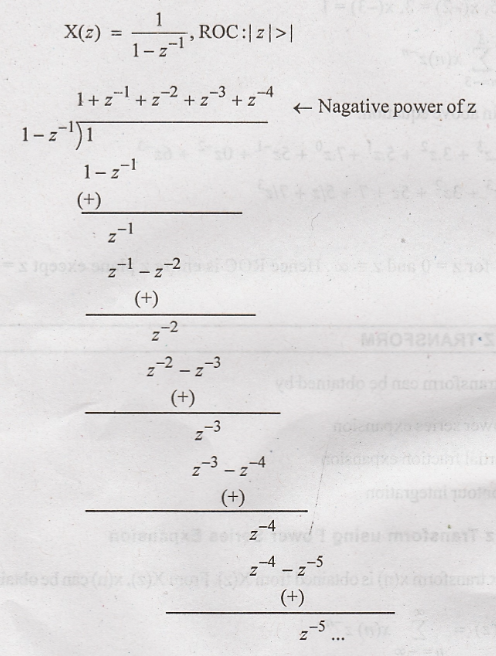
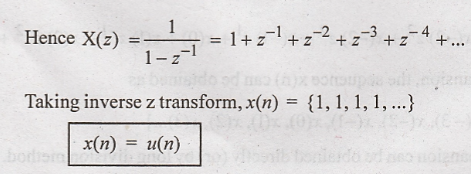
Problem 2:
Determine
inverse z transform of X(z) = 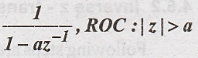
Solution:
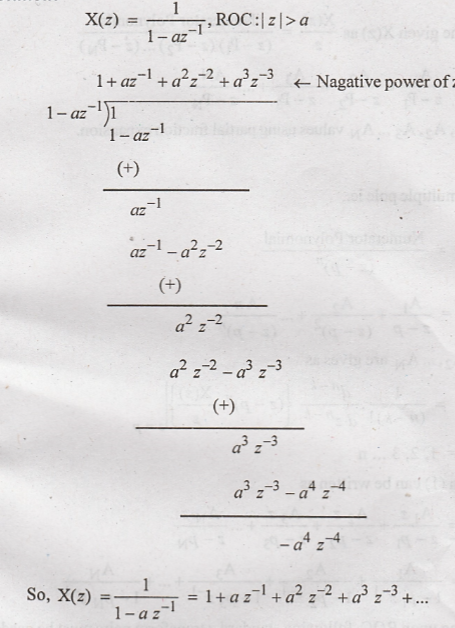
Taking
inverse z transform, x(n) = {1, a, a2, a3,...} = an
u(n)
Hint:
When ROC is |z|>|a| (or) |z| > 1, we should expand, X(z) in negative
powers of z.
Inverse z - transform using partial fraction expansion
Following
steps are performed for partial fraction expansion case I
Case I:
I
Step: Arrange the given 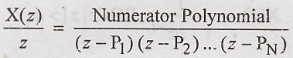
II
Step: 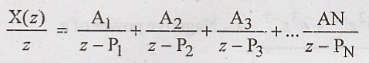
Then
find A1, A2, A3 ... AN values using
partial fraction expansion.
Case II
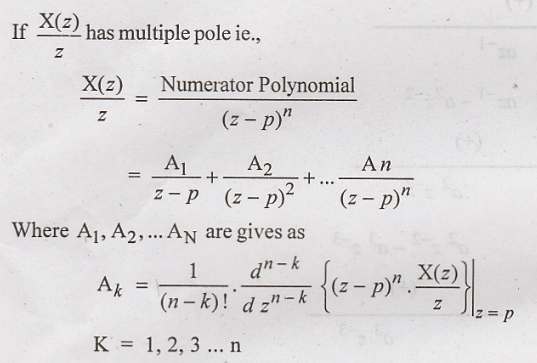
III
Step: Equation (1) can be written as
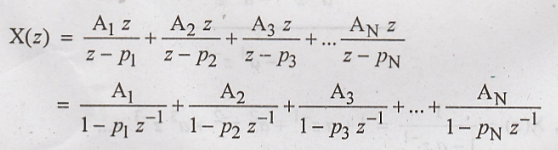
IV
Step: Depending upon ROC, following standard z transform pairs must be used.
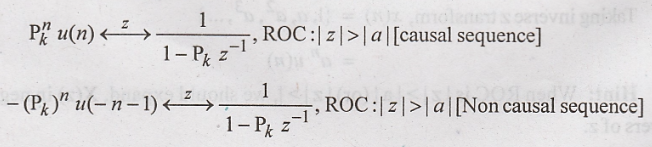
Problem 1:
Determine
the inverse z transform of X(z) = 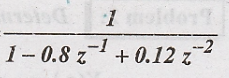 ROC is z > 0.6.
ROC is z > 0.6.
Solution:
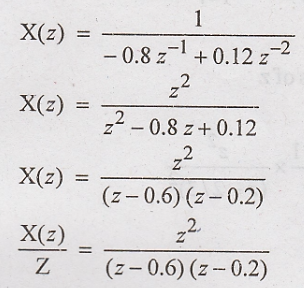
By
partial fraction technique we get
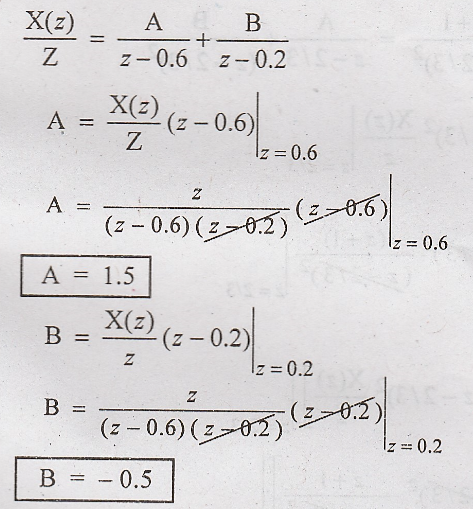
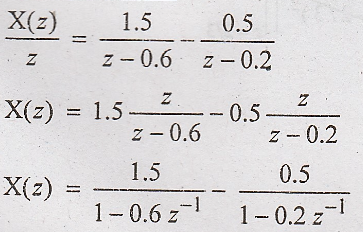
Taking
inverse z transform using standard relation, we get
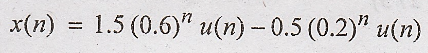
Problem 2:
Determine
the inverse z transform of
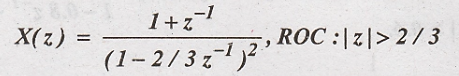
Solution:
Convert
X(z) to positive powers of z
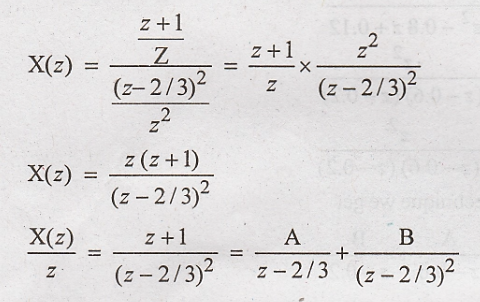
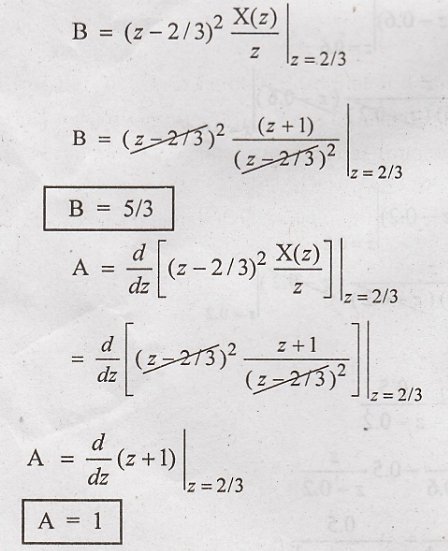
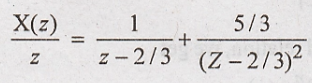
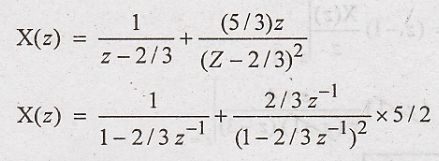
Taking
inverse z transform using standard relations
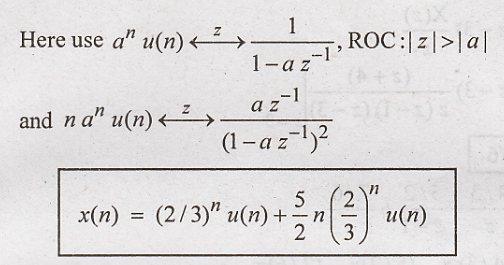
Problem 3:
Find
the inverse z transform of X(z) = 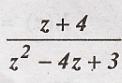
Solution:
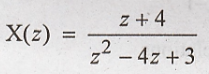
Divide
the above equation by z in order to get X(z)/z
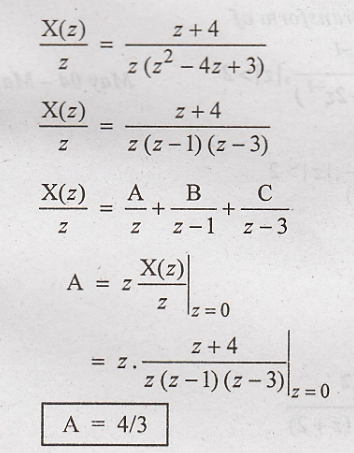
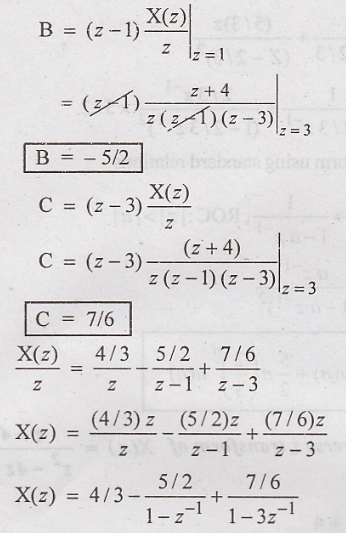
Taking
inverse z transform using standard relations
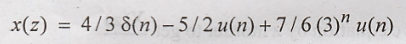
Problem 4:
Find
the inverse z transform of
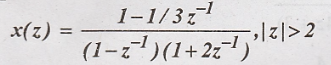 May 04 – Marks 10
May 04 – Marks 10
Solution:
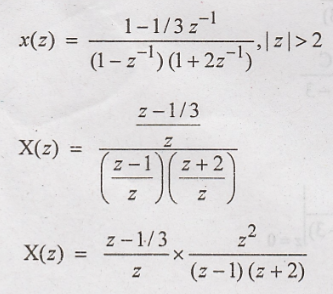
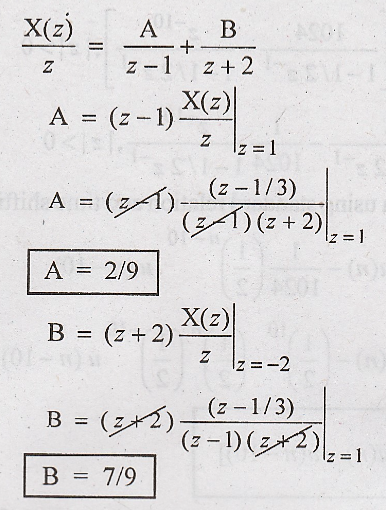
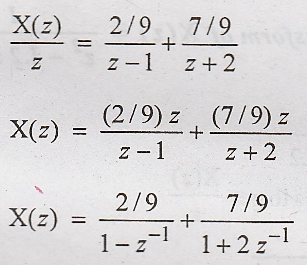
Taking
inverse z transform using standard relation.
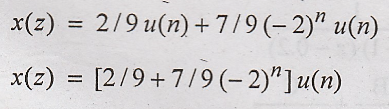
Problem 5:
Find
the inverse z transform of
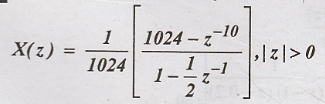 May 12-Marks 8
May 12-Marks 8
Solution:
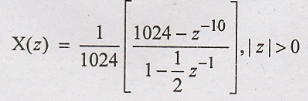
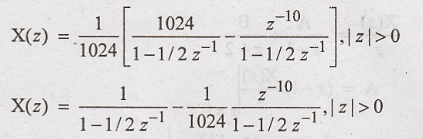
Taking
inverse z transform using standard relation and time shifting property.
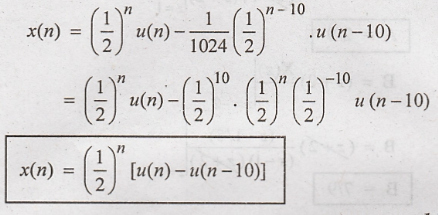
Problem 6:
Find
the inverse z transform of X(z) = 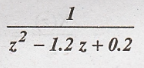
Solution:
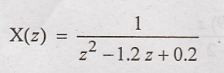
Divide
above equation by z in orders to get X(z)/z
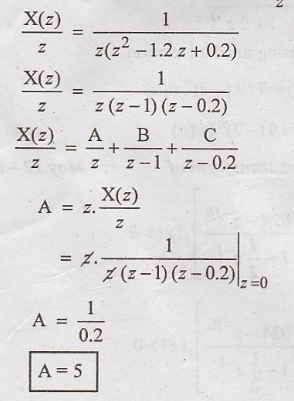
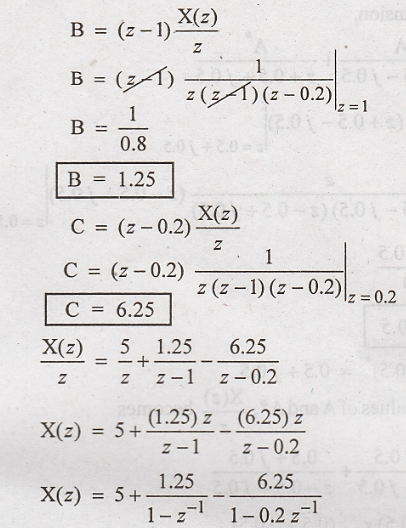
By
taking inverse z transform using standard relations
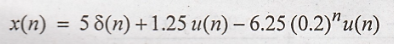
Problem 7:
Determine
inverse z transform of the following function
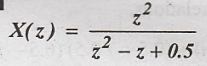
Solution:
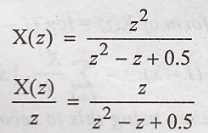
Roots
of quadratic equation
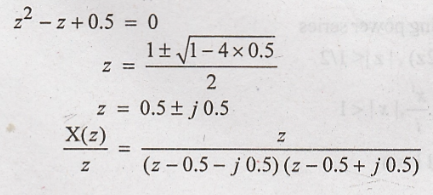
By
partial fraction expansion,
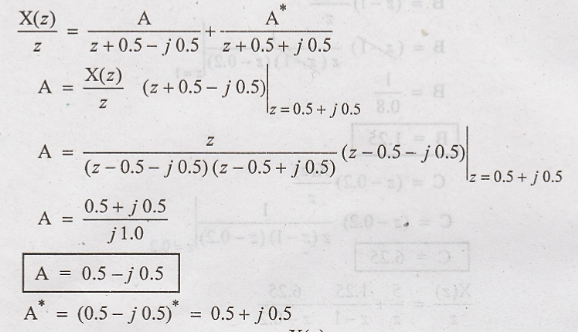
After
substituting the values of A and A*, X(z)/z becomes
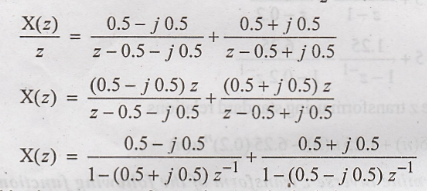
Taking
inverse z transform using standard relations,
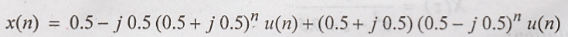
Problem 8:
Determine
the inverse z transform of X(z) = log (1-2z), |z| < 1/2 by using the power
series log (1 − x) = 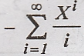 , |x| < 1 and by first differentiating X(z)
and then using this to recover x(n).
, |x| < 1 and by first differentiating X(z)
and then using this to recover x(n).
Solution:
Inverse
z transform using power series
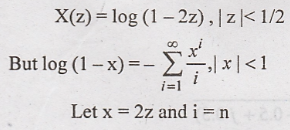
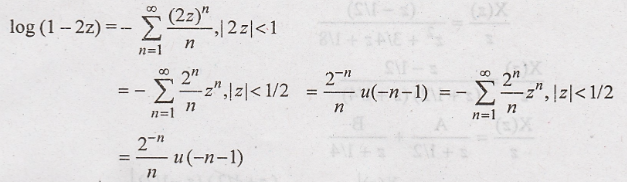
Inverse
z transform using differentiation
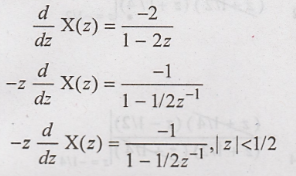
Taking
inverse z transform on both sides
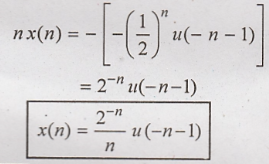
Problem 9:
Find
the inverse z transform of the following.
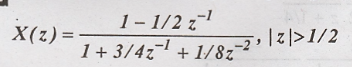
Solution:
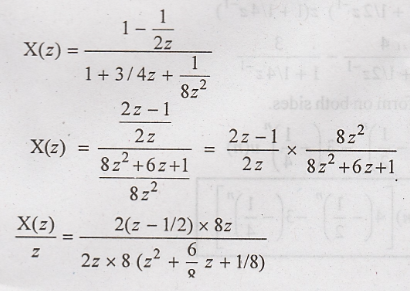
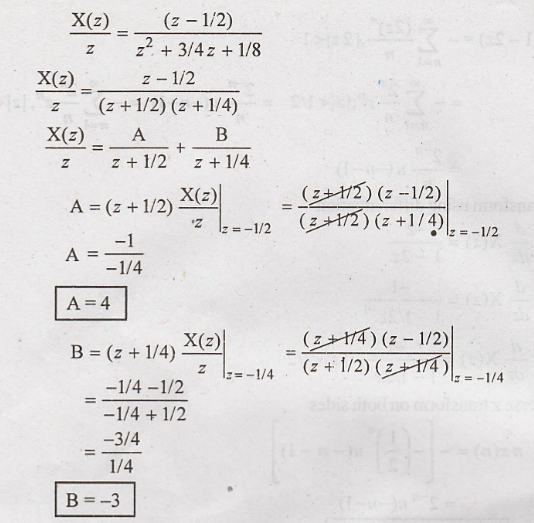
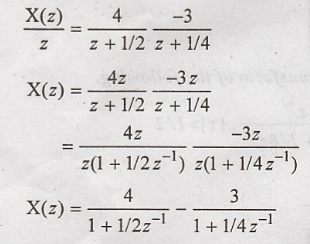
Taking
inverse z transform on both sides.
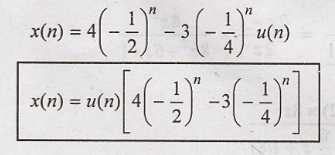
Problem 10:
Find
the inverse z transform of the following. Dec-10, 5marks
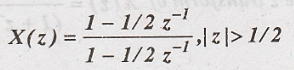
Solution:
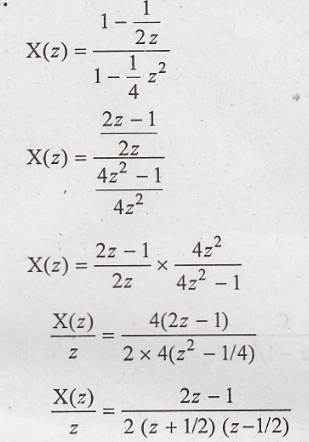
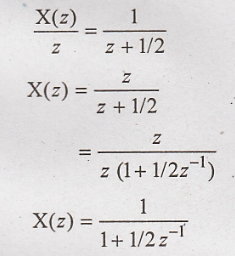
Taking
inverse z transform using standard relationship
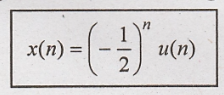
Problem 11:
Determine
inverse z transform of X(z) = 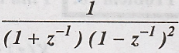 ROC:|z|>1
ROC:|z|>1
Solution:
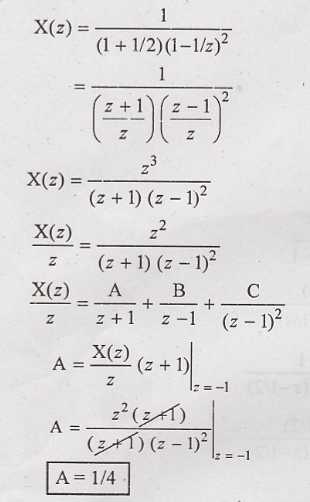
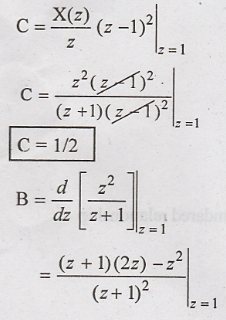
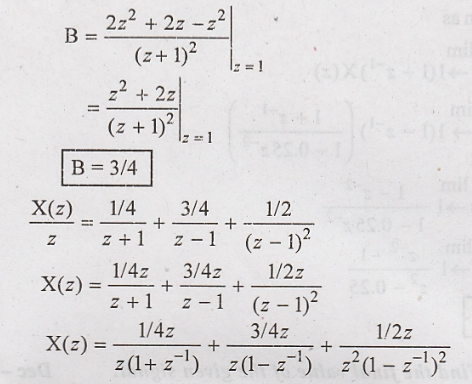
Taking
inverse z transform using standard relation,
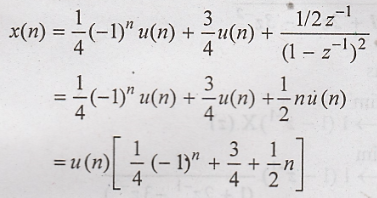
Problem 12:
Find
the initial and final values of the function.
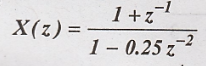 (May-97)
(May-97)
Solution:
Initial
value is given as
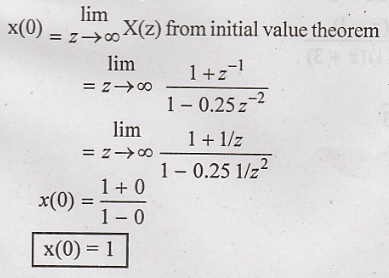
Final
value is given as
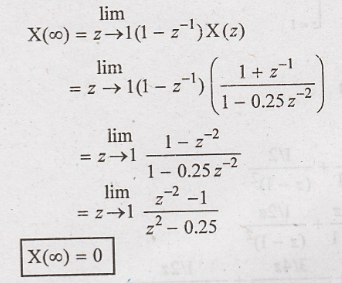
Problem 13:
Find
the final value of the given signal.
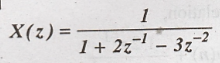 Dec-03/3 marks
Dec-03/3 marks
Solution:
Final
value is given as
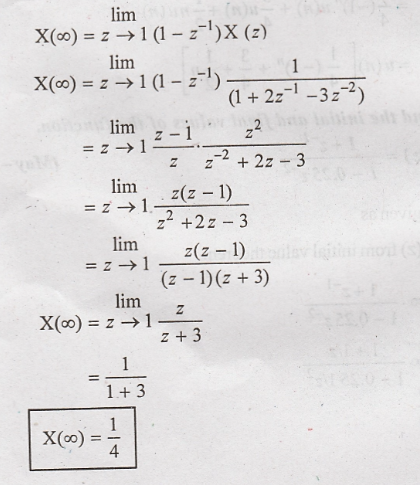
Signals and Systems: Unit IV: Analysis of Discrete Time Signals,, : Tag: : Inverse z Transform using Power Series Expansion, Inverse z-transform using partial fraction expansion - Inverse Z Transform
Related Topics
Related Subjects
Signals and Systems
EC3354 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
