Random Process and Linear Algebra: Unit V: Linear Transformation and Inner Product Spaces,,
Invariant
Definitions and problems on Invariant
(e) Invariant
Definitions :
Let V be a vector space, and let T : V → V be
linear. A subspace W of V is said to be T-invariant if T(x) Є W for every x Є
W, that is T(W) ![]() W. If W is T-invariant, we define the restriction of T
on W to be the function TW : W → W defined by TW (x) =
T(x) for all x Є W.
W. If W is T-invariant, we define the restriction of T
on W to be the function TW : W → W defined by TW (x) =
T(x) for all x Є W.
Problem 1.
If W is a subspace of a vector space V and that T :
V → V is linear.
Prove that subspace {0}, V, R(T), and N(T) are all
T-invariant.
Solution :
A subspace W of the vector space V is said to be
T-invariant if T(x) Є W for every x Є W, that is T(W) ![]() W.
W.
If W is T-invariant, define the restriction of T on
W be the function TW : W → W defined by Tw(x) = T(x) for
all x Є W, where T: V → V is linear.
Let the subspace W = {0}
Since T is linear, based on the property of
linearity.
=> T(0) = 0, that is T(x) Є W
=> W = {0} is T-invariant by definition of
T-invariant.
Let the subspace W = V.
Since T is defined as T : V → V, therefore T(V) ![]() V.
V.
=> W = V is T-invariant by the definition of
T-invariant.
Let the subspace W = R(T).
Let x Є R(T), that is some y Є V exists such that
T(y) = x
Now, take the function T on both sides of T(y) = x,
to get the following:
T(T(y)) = T(x)
Since T(y) Є V, T(x) Є R(T) and so, T(R(T)) C R(T)
W = R(T) is T-invariant by the definition of
T-invariant.
Let the subspace W = N(T).
Let x Є N(T), that is T(x) = 0

W = N(T) is T-invariant by the definition of
T-invariant.
Problem 2.
If W is T-invariant, prove that Tw is
linear.
Solution :
To show that Tw is a linear if W is
T-invariant.
A subspace W of the vector space V is said to be
T-invariant if T(x) Є W for every x Є W, that is T(W) ![]() W.
W.
If W is T-invariant, define the restriction of T on
W to be the function TW : W →
W defined by TW(x) = T(x) for all x Є W, where T : V → V is linear.
Let x, y Є W
Since W ![]() V, so x,y Є V and for all x,y Є W
V, so x,y Є V and for all x,y Є W
As T is linear on V,
. '.T(x + y) = T(x) + T(y)
T(α x) = α T(x), for α Є F
Thus, T is linear on W and hence TW is
linear.
Problem 3.
Suppose that T is the projection on W along some
subspace W'. Prove that W is T-invariant and that TW = IW.
Solution :
To show that W is T-invariant and that TW
= IW, if T is the projection on W along some subspace W'.
We know that, T : V → V is called the projection on
W1 along W2 if, for x = x1 + x2
with x1 Є W1 and x2 Є W2.
We have T(x) = x1, where W1
and W2 are the subspaces of the vector space V such that 

Since T is the projection on W along some subspace
W', therefore using definition of projection
We have T(y) = y for all y Є W that is T(W) ![]() W.
W.
By the definition of T-invariant, => W is
T-invariant.
Problem 4.
Suppose that V = R(T) ![]() W and W is
T-invariant.
W and W is
T-invariant.
Prove that W ![]() N(T)
N(T)
Solution :
Let T : V → V be a linear transformation.
Let W is a T-invariant subspace of V = R(T) ![]() W.
W.
Here, W is a T-invariant, then T(W) ![]() W.
W.

Here, W is a subspace of V => W C V
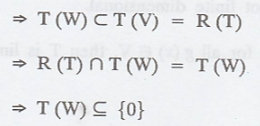
That is, for each w in W. T(W) = 0
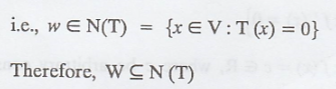
Problem 5.
Suppose that V = R(T) ![]() W and W is T-invariant.
W and W is T-invariant.
(i) Show that if V is finite-dimensional, then W =
N(T)
(ii) Show by example that the conclusion of (i) is
not necessarily true if V is not finite-dimensional.
Solution :
(i) Let V is a finite dimensional vector space.
By Dimension Theorem,
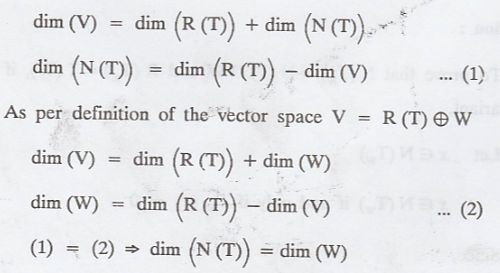
(ii) Let V be a set of all polynomials over the
field R is a vector space, then clearly V is not finite dimensional.
Define T(g(x)) = g'(x), for all g(x) Є V, then T is
linear.
Now,

Therefore, the conclusion of part (i) is not
necessarily true if V is not finite-dimensional.
Problem 6.
Suppose that W is T-invariant. Prove that N(TW)
= N(T) ∩ W and R(TW) = T(W)
Solution :

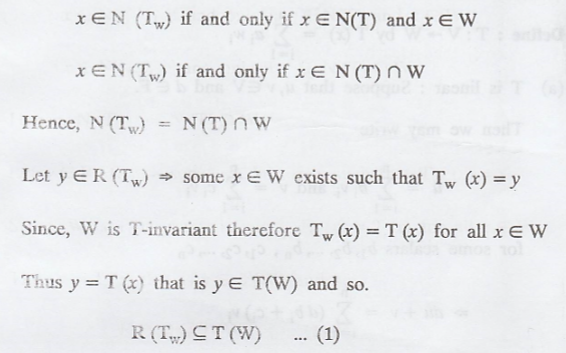
Converse
part:
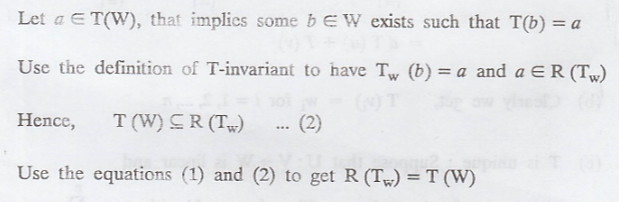
Random Process and Linear Algebra: Unit V: Linear Transformation and Inner Product Spaces,, : Tag: : - Invariant
Related Topics
Related Subjects
Random Process and Linear Algebra
MA3355 - M3 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
