Introduction of Vector Spaces

VECTOR SPACES

Introduction      

In this section, we introduce the underlying structure of linear algebra, that of a finite dimensional vector space.

The definition of vector space V, whose elements are called vectors, involves an arbitrary field F, whose elements are called scalars.

The following notations will be used

Vector Spaces

Definition : Vector space or linear space :

A vector space V over a field F consists of a set on which two operations (+ and .) are defined so that for each pair of elements (x, y) in V there is a unique element x + y in V and for each element a in F and each element x in V there is a unique element ax in V, such that the following axioms hold.

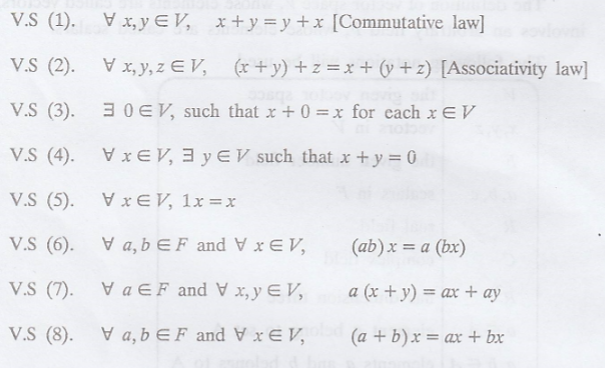
Example : R, R², R³, Rⁿ are the vector spaces over R

Note:

(1) The elements of the field F are called scalars and the elements of the vector space V are called vectors.

(2) An object of the form (a₁, a₂, ..., a_n) where the entries a₁, a₂,...,a_n are elements of F, is called an n-tuple space with entries from F.

(3) Two n-tuples (a₁, a₂, ..., a_n) and (b₁, b₂, ..., b_n) with entries from a field F are equal if a_i = b_i for i = 1,2,...n

(4) The set of all n-tuples with entries from a field F is denoted by Fⁿ.

(5) Vectors in Fⁿ may be written as column vectors 

Theorem: [Cancellation law for vector addition]

If x, y, z are vectors in a vector space V such that x + z = y + z, then x = y

Proof :

Given: x + z = y + z, for all x,y,z ε V ...... (1)

To prove : x = y

Proof: We know that

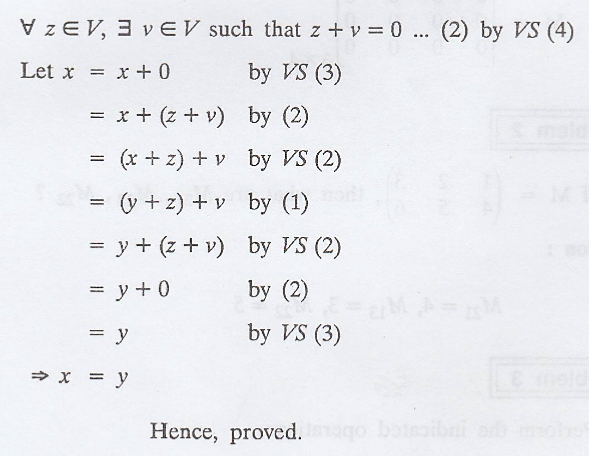
Note: If x, y, z are vectors in a vector space V, then

(i) x + y = x + z => y = z

(ii) y + x = z + x => y = z