Introduction of Random Processes

RANDOM PROCESSES

Introduction

A random process is conceptually an extension of a random variable.

A random variable is a function of time is called a random process.

New problems in various branches of Engineering and Science, do not fit into the frame work of the classical probability theory. Such problems arouses us to study the processes, that is, phenomena that takes place in time. It is necessary to develop random processes which is a family of random variables that is indexed by a parameter such as time. Many problems that arise in Physics, Chemistry and other fields can be solved by using random processes. In this unit, we give a simple solution to the mathematical problems which use random processes technique.

A comparison of Random variable and random process.

DEFINITION AND EXAMPLES

(a) Random process

A random process is a collection (or ensemble) of random variables {X(s, t)} that are functions of a real variable, namely time 't' where s ε S (Sample space) and t ε T (parameter set or index set)

Examples:

1. The daily stock price.

2. The wireless signal received by a cell phone over time.

3. The image intensity over 1 c.m2 regions.

State space

The set of possible values of any individual member of the random process is called state space.

Any individual member itself is called a sample function or a realisation of the processes.

Note

(i) If 's' and 't' are fixed, {X(s, t)} is a number,

(ii) If 't is fixed, {X(s, t)} is a random variable.

(iii) If 's' is fixed. {X(s, t)} is a single time function.

(iv) If 's' and ' are variables, {X(s, t)} is a collection of random variables that are time functions.

Notation: As the dependence of a random process on 's' is obvious, 's' will be omitted in the notation of a random process. If the parameter set 'T' is discrete, the random process will be noted by {X(n)} or Xn. If the parameter set 'T' is continuous, the process will be denoted by {X(t)}.

(b) Classification of process [A.U CBT Dec. 2009] [A.U A/M 2019 (R13) RP]

It is convenient to classify random processes according to the characteristics of t and the random variable X = X(t) at time t. We shall consider only four cases based on t and X having values in the ranges -∞ < t < ∞ and - ∞ < x < ∞

1. Continuous random process

2. Continuous random sequence

3. Discrete random process

4. Discrete random sequence

We can classify random process in another way also. It can be classified as

1. Deterministic random process

2. Non-deterministic random process

(c) Statistical (Ensemble) Averages

(i) Mean = E [X (t)] =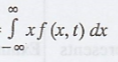 

(ii) Auto correlation function of [X (t)]

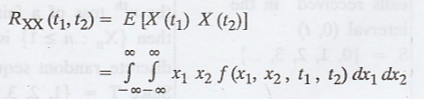
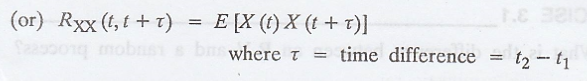
(iii) Auto covariance of [X (t)]

(iv) Correlation coefficient of [X (t)]

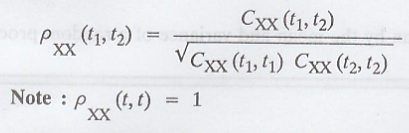
(v) Cross correlation

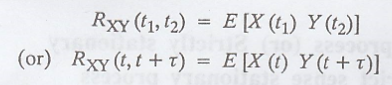
(vi) Cross covariance

(vii) Cross correlation coefficient

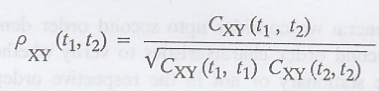
Example 3.1.1.

Define a random process. Explain the classification of random process. Give an example to each case. [A.U. N/D 2003]

Solution :

It is convenient to classify random processes according to the characteristics of t and the random variable X = X(t) at time t. We shall consider only four cases based on t and X having values in the ranges -∞ < t < ∞ and - ∞ < x < ∞

1. Continuous random process

2. Continuous random sequence

3. Discrete random process

4. Discrete random sequence

EXERCISE 3.1

1. What is the difference between an R.V and a random process?

2. What is the difference between random sequence and random processes?

3. What is a discrete random sequence? Give an example.

4. What is a continuous random sequence? Give an example.

5. What is a continuous random process? Give an example.

6. What do you mean by the mean and variance of a random process?