Signals and Systems: Unit IV: Analysis of Discrete Time Signals,,
Introduction of Analysis of Discrete Time Signals
Baseband Sampling
Most of the signals encountered in nature are continuous in time but in digital signal processing the signals are sampled and quantized at discrete-time instants and are represented as a sequence of 1's and O's. For example, signal such as speed signal, ECG and EEG are electrical signals and therefore necessary to perform a conversion to digital representation. This can be done by an analog to digital representation. This can be done by an analog to digital converter.
INTRODUCTION OF ANALYSIS OF DISCRETE TIME SIGNALS
Most
of the signals encountered in nature are continuous in time but in digital
signal processing the signals are sampled and quantized at discrete-time
instants and are represented as a sequence of 1's and O's. For example, signal
such as speed signal, ECG and EEG are electrical signals and therefore
necessary to perform a conversion to digital representation. This can be done
by an analog to digital representation. This can be done by an analog to digital
converter.

The
above figure shows the ADC unit and its constituent parts. The sampler, samples
the input signal with a sampling interval T, producing an output x(nT). The
signal x(nT) is discrete in time but continuous in amplitude. The output of the
sampler is applied to a quantize. It converts x(nT) into discrete time,
discrete-amplitude signal. After sampling and quantization, the final step in
converting an analog signal to a form acceptable to digital computer is called
coding. The coder maps each quantized sample value in digital world.
A
continuous time signal can be represented in the frequency domain using Laplace
transform or continuous-time Fourier transform (CTFT). Similarly, a discrete
time signal can be represented in the Frequency domain using Z- transform or
discrete time Fourier transform. The Fourier transform of a discrete time
signal is called discrete time Fourier transform (DTFT).
BASEBAND SAMPLING
Sampling Theorem for Lowpass (LP) Signals
Statement of sampling
Theorem:
1.
A band limited signal of finite energy, which has no frequency components
higher than W hertz, is completely described by specifying the values of the
signal at instants of time separated by 1/2W seconds.
2.
A bandlimited signal of finite energy, which has no frequency components higher
than W hertz, may be completely recovered from the knowledge of its samples
taken at the rate of 2W samples per second.
The
first part of above statement tells about sampling of the signal and second
part tells about reconstruction of the signal. Above statement can be combined
and stated alternatively as follows:
A
continuous time signal can be completely represented in its samples and recoved
back if the sampling frequency is twice of the highest frequency content of the
signal i.e.,
fs
≥ 2W
Here
fs ⇒
Sampling frequency
W
⇒ Higher frequency
content
Proof of Sampling
theorem:
There are two parts:
(i)
Representation of x(t) intems of its samples.
(ii)
Reconstruction of x(t) from its samples.
Part I:
Representations of x(t) intems of its samples. x(n Ts)

The
sampled singal xδ (t) is given as

Step 2: 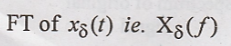
Taking
FT of equation
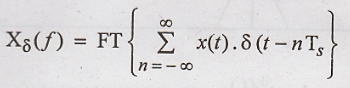
We know that FT of product in time domain becomes convolution in frequency domain. i.e.,
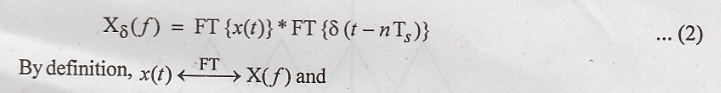
Hence
equation (2) becomes,
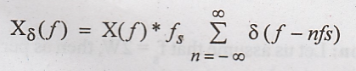
Since
convolution is linear
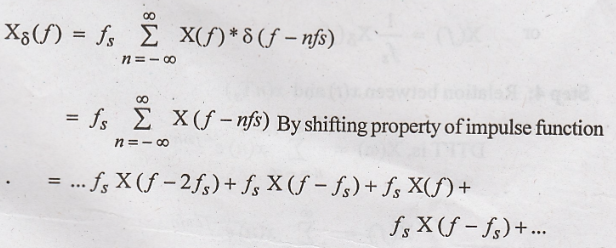
Comments:
(i)
The RHS of above equation shows that X(f) is placed at 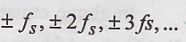
(ii)
This means X(f) is periodic in fs.
(iii)
If sampling frequency is fs = 2W, then the spectrum X(f) just touch
each other.
Step 3:
Relation between X(f) and Xδ(f).
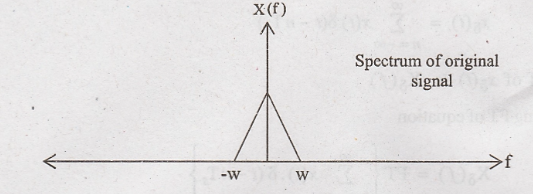
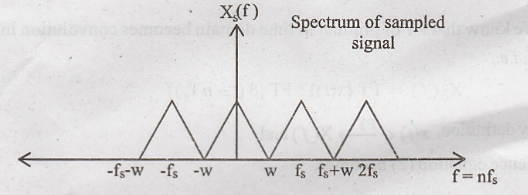
Important
assumption: Let us assume that fs = 2W, then as per above diagram,
Step 4:
Relation between x(t) and x(nTs).
In
above equation f is the frequency of DT signal. If we replace X(f) by Xδ(f),
then 'f becomes frequency of CT signal i.e.,
In
above equation f is frequency of CT signal and f/fs = frequency of
DT signal in equation since x(n) = x(nTs), i.e. samples of x(t),
then
Putting
above expression in equation (3)
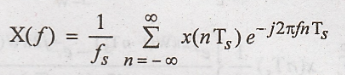
Inverse
Fourier transform (IFT) of above equation gives x(t) i.e.,
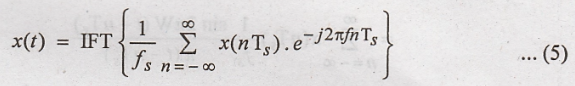
Comments:
i)
Here x(t) is represented completely interms of x(nTs).
ii)
Above equation holds for fs = 2W. This means if the samples are
taken at the rate of 2W or higher, x(t) is completely represented by its
samples.
iii)
First part of the sampling theorem is proved by above two comments.
Part-II:
Reconstruction of x(t) from its samples.
Step
1: Take inverse Fourier transform of X(f) which is interms of Xδ(f).
Step
2: Show that x(t) is obtained back with the help of interpolation function.
Step
1: The IFT of equation (5) becomes,
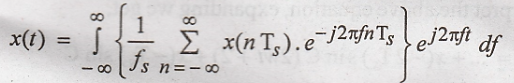
Here
the integration can be taken from - W ≤ f ≤ W.
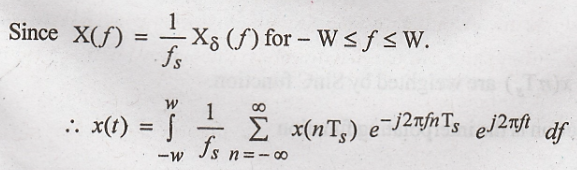
Interchanging
the order of summation and integration,
Simplifying
above equation,
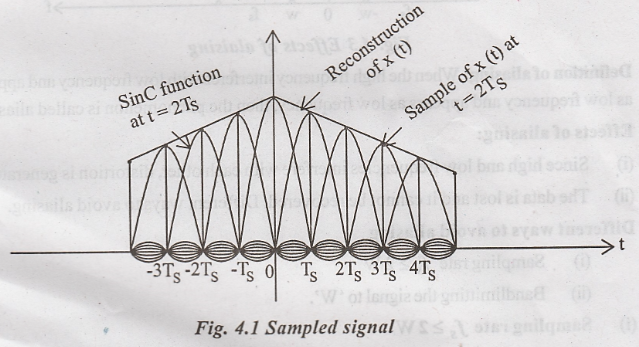
Step 2:
Let as interpret the above equation, expanding we get,
Comments:
(i)
The samples x(nTs) are weighted by SinC function.
(ii)
The SinC function is the interpolating function
Step 3:
Reconstruction of x(t) by low pass filter
Effects of Undersampling (Aliasing)
While
proving sampling theorem we considered that fs = 2W consider the
case of fs < 2 W, then spectrum of Xδ(f) will be
modified as follows:
(i)
The spectrum located at X(ƒ), X(f − ƒs), X(ƒ −2ƒs), ...
overlap on each other.
(ii)
Consider the spectrums of X(f) and X(f - fs) is magnified.
(iii)
The high frequencies near 'ω' in X(f - fs) overlap with low
frequencies (fs - W) in X(f).
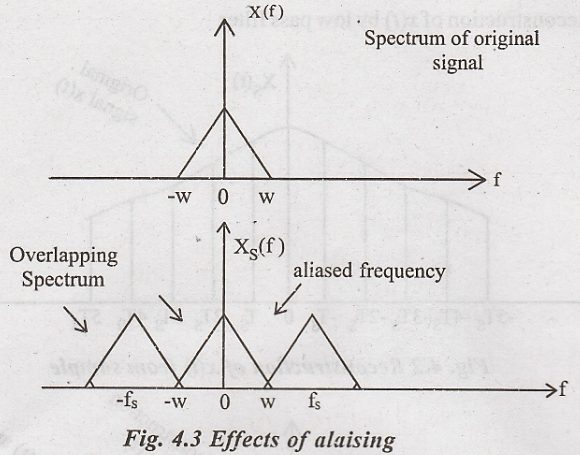
Definition of aliasing:
When the high frequency interferes with low frequency and appears as low
frequency and appears as low frequency, then the phenomenon is called aliasing.
Effects of aliasing:
(i)
Since high and low frequencies interfere with each other, distortion is
generated.
(ii)
The data is lost and it cannot be recovered. Different ways to avoid aliasing.
Different ways to
avoid aliasing
(i)
Sampling rate fs ≥ 2W
(ii)
Bandlimitting the signal to 'W'.
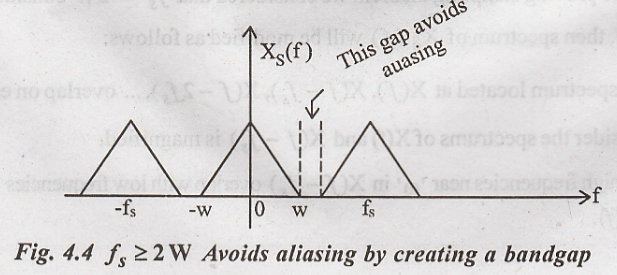
(i) Sampling rate fs ≥ 2W
When
the sampling rate is made higher than 2W, then the spectrums will not overlap
and there will be sufficient gap between the individual spectrum.
(ii) Bandlimitting the signal
The
sampling rate is, fs = 2 W. There can be for components higher than
2W. These components creating aliasing. Hence a low pass filter is used before
sampling the signal as shown in figure.

Nyquist rate and Nyquist interval
Nyquist rate:
When the sampling becomes exactly equal to '2W' samples/sec, for a given
bandwidth of W hertz, then it is called Nyquist rate.
Nyquist interval:
It is the time interval between any two adjacent samples when sampling rate is
Nyquist rate.
Nyquist
rate = 2W Hz
Nyquist
interval = 1/2W seconds
Problem based on
sampling theorem
Problem 1:
A
signal having a spectrum ranging from near dc to 10KHz is to be sampled and
converted to discrete form. What is the minimum number of samples per second
that must be taken to ensure recovery?
Solution:
Given:
fm = 10 KHz
From
Nyqulist rate, the minimum number of samples that must be taken to ensure
recovery is,
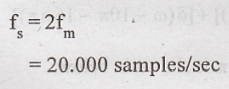
Problem 2:
The
signal x(t) = 10 cos (10πt) is sampled at a rate 8 samples per second. Plot the
amplitude spectrum for w≤ 30 π. Can the original signal can be recovered from
samples? Explain.
Solution:
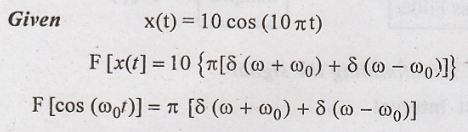
The
amplitude spectrum shown below
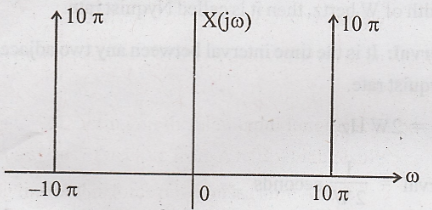
The
sampling rate is less than Nyquist rate. So, the original signal cannot be
recovered from the samples.
The
frequency spectra of sampled x(t) is given by
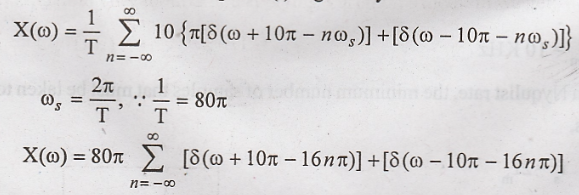
The
plot of amplitude spectrum for |ω|≤ 30 π is shown in below
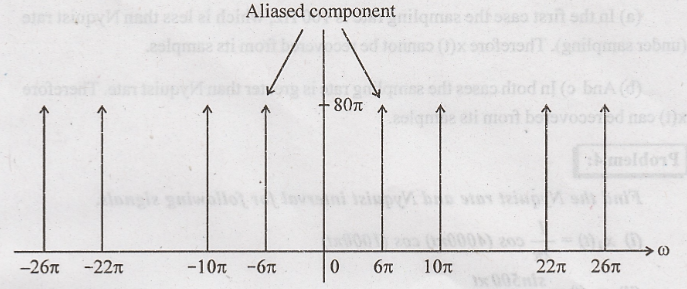
Problem 3:
A
signal x(t) = sin C (150 πt) is sampled at a range of (a) 100 Hz (b) 200 Hz (c)
300 Hz. For each of these three cases, explain if you can recover the signal
x(t) from the sampled signal.
Solution:
Given:
x(t) = sinС (150 πt)
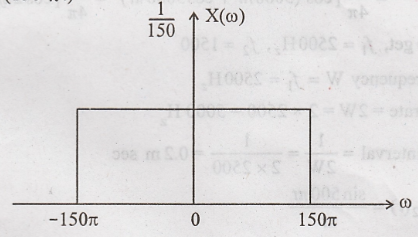
The
spectrum of the signal x(t) is a rectangular pulse with a bandwidth (maximum frequency
component) of 150 π rad/sec.
From
the above figure, we have
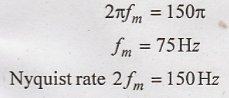
(a)
In the first case the sampling rate is 100 Hz, which is less than Nyquist rate
(under sampling). Therefore x(t) cannot be recovered from its samples.
(b)
And c) In both cases the sampling rate is greater than Nyquist rate. Therefore
x(t) can be recovered from its samples.
Problem 4:
Find
the Nyquist rate and Nyquist interval for following signals.
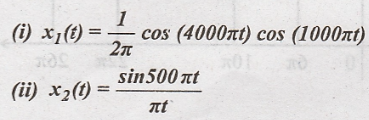
Solution:
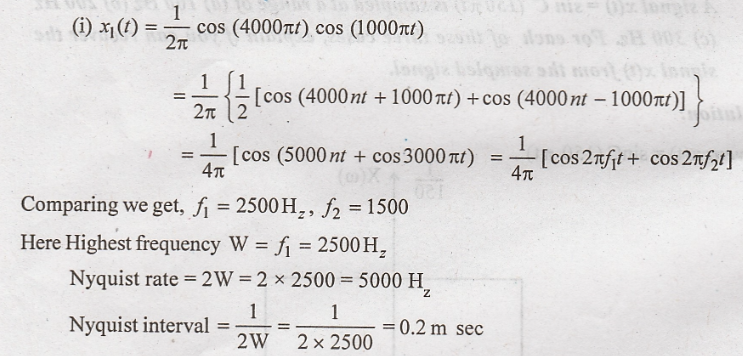
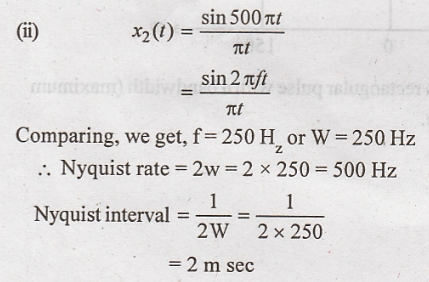
Problem 5:
Determine
the Nyquist sampling rate and Nyquist sampling interval for following signals:
(i)
x(t) = sin C2 (200t)
(ii)
x(t) = 25 cos (500 πt)
Solution:
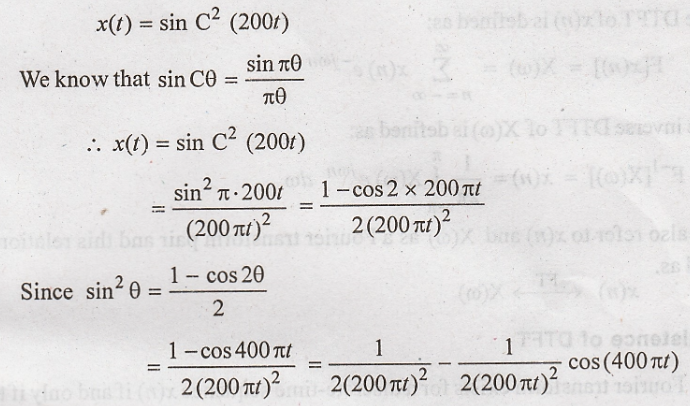
compare
above equation with,
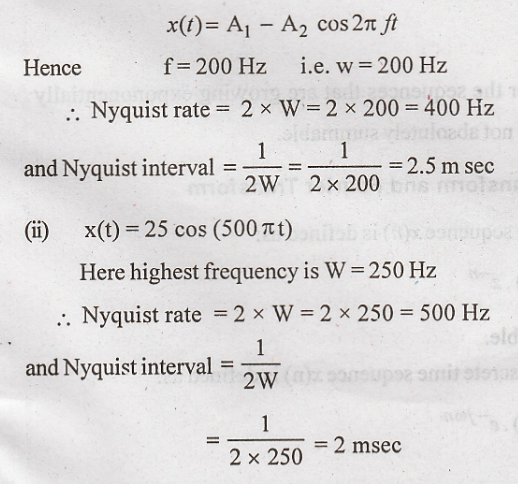
Signals and Systems: Unit IV: Analysis of Discrete Time Signals,, : Tag: : Baseband Sampling - Introduction of Analysis of Discrete Time Signals
Related Topics
Related Subjects
Signals and Systems
EC3354 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
