Random Process and Linear Algebra: Unit V: Linear Transformation and Inner Product Spaces,,
Inner Product spaces Orthogonal sets R2, R3, R4, C4, P(R)
Problems under Inner product spaces Orthogonal sets R2, R3, R4, C4, P(R)
(b) Inner
product spaces Orthogonal sets R2, R3, R4, C4,
P(R)
Problem 1.
Apply the Gram-Schmidt
process to the given subset S = {(1, 0, 1), (0, 1, 1), (1, 3, 3)} and x = (1,
1, 2) of the inner product space V = R3
(a) to obtain an
orthogonal basis for span (S)
(b) Normalize the
vectors in this basis to obtain an orthonormal basis β for span (S)
(c) Compute the Fourier
coefficients of the given vector relative to β.
Solution
:
(a) Apply Gram-Schmidt
process
(b) The vectors v1,
v2 and v3 can be normalized to obtain the orthonormal
basis {u1, u2, u3},
where,
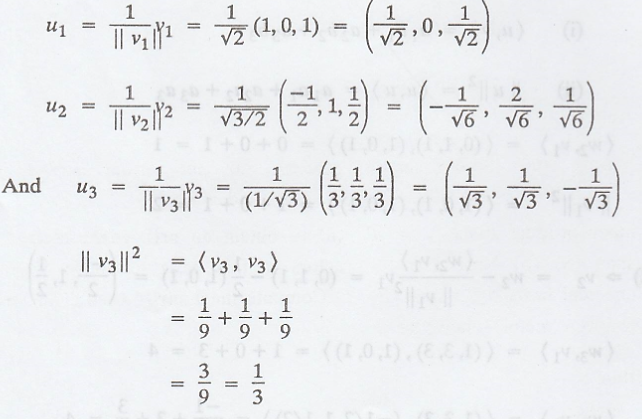
Hence, the required
orthonormal basis of span(S) is :
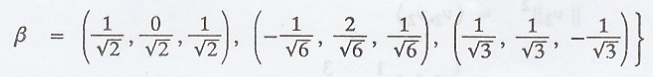
(c) Now, find the
Fourier coefficients for, x = (1, 1, 2)
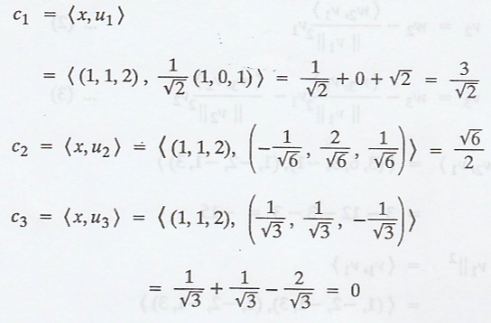
Hence, the required
Fourier coefficients are :
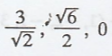
Problem 2.
Apply the Gram-Schmidt
process to the given subset S = {(1, -2, -1, 3), (3, 6, 3, −1), (1, 4, 2, 8)}
and x = (-1, 2, 1, 1) of the inner product space V = R4 (a) to
obtain an orthogonal basis for span (S) (b) Normalize the vectors in this basis
to obtain an orthonormal basis β for span (S) (c) Compute the Fourier
coefficients of the given vector relative to β.
Solution
:
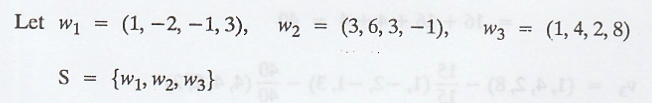
(a) Apply Grass-Schmidt process
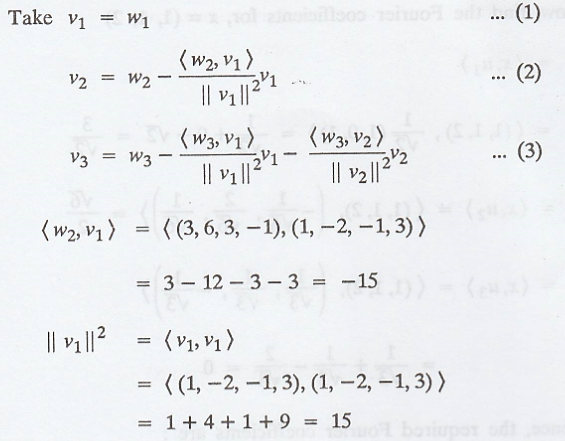
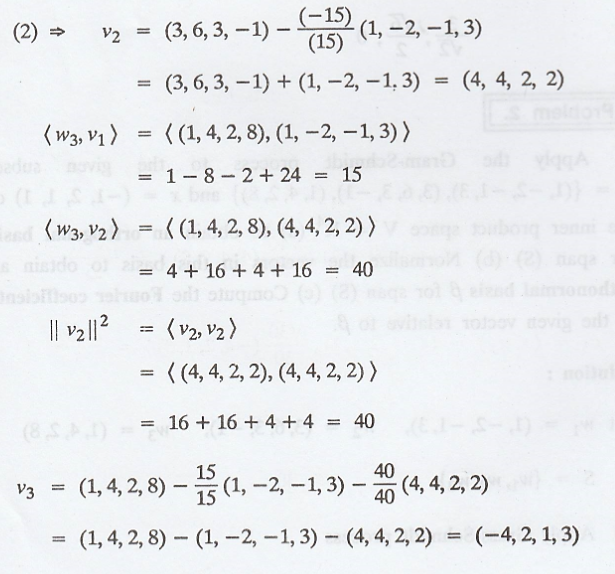
(b) The vectors v1,
v2 and v3 can be normalized to obtain the orthonormal
basis {u1, u2, u3}, where
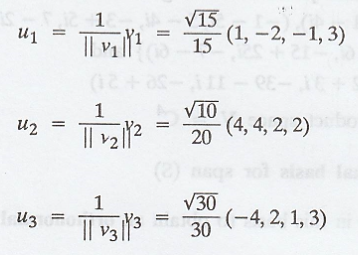
Thus, the required
orthonormal basis of span(S) is,
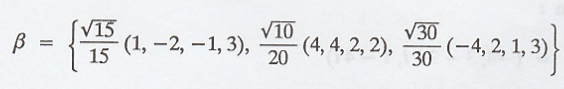
(c) Next compute the
Fourier coefficients for,
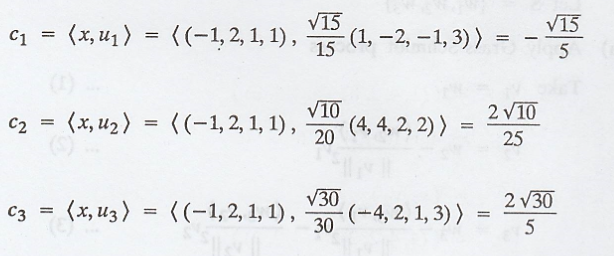
Hence, the required of
Fourier coefficients are,
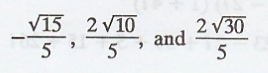
Problem 3.
Apply the Gram-Schmidt
process to the given subset
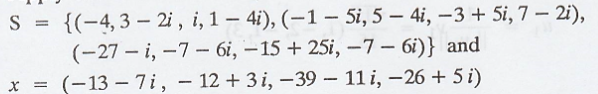
of the inner product
space V = C4
(a) to obtain an
orthogonal basis for span (S)
(b) Normalize the
vectors in this basis to obtain an orthonormal basis β for span (S)
(c) Compute the Fourier
coefficients of the given vector relative to β.
Solution
:
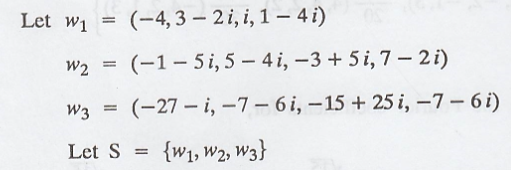
(a) Apply Grass-Schmidt
process
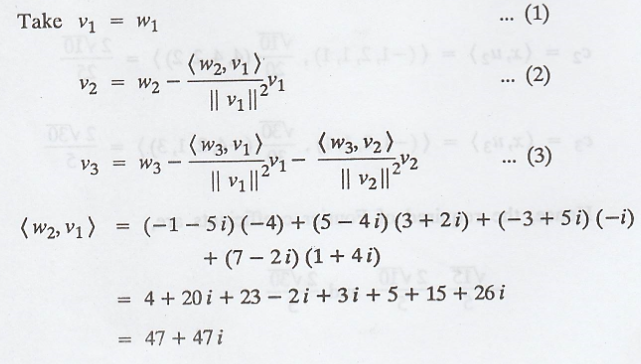
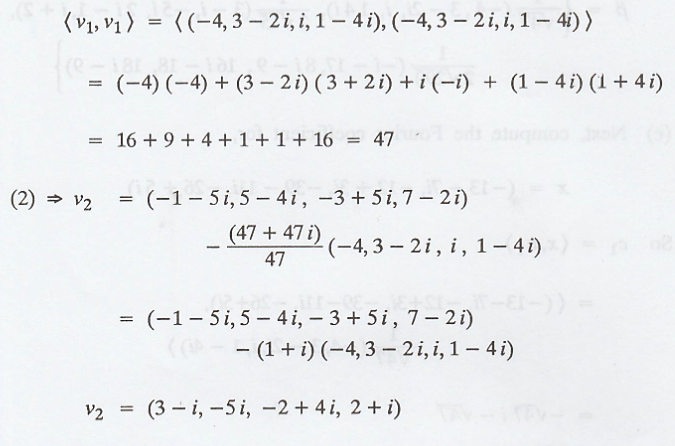
Similarly,
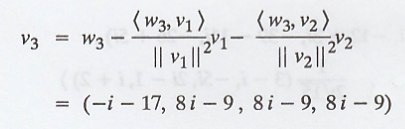
(b) The vectors v1
and v3 can be normalized to obtain the orthonormal basis {u1,
u2, u3}, where,
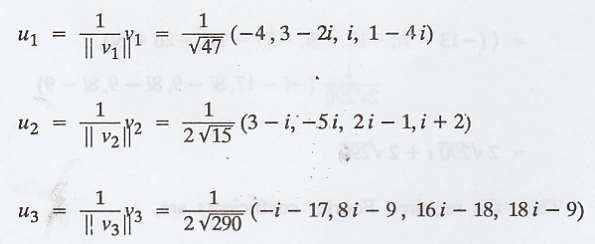
Hence, the required
orthonormal basis of span(S) is,
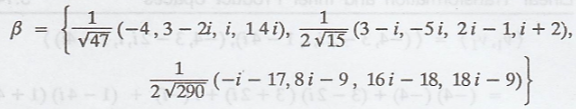
(c) Next, compute the
Fourier coefficient for,
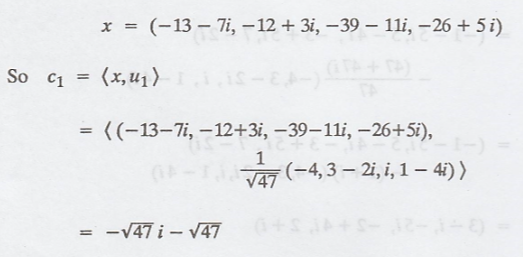
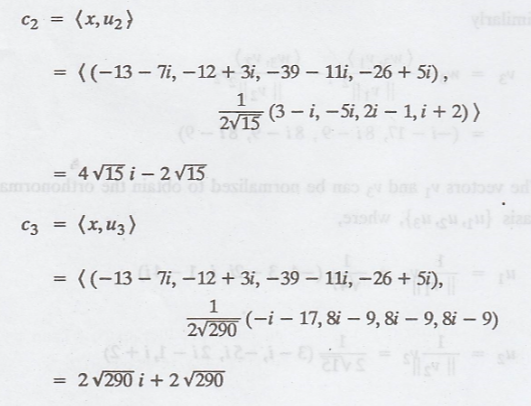
Thus, the required
Fourier coefficients are,
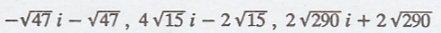
Problem 4.
In R2, let
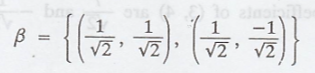
Find the Fourier
coefficients of (3, 4) relative to β
Solution
:
Let the set 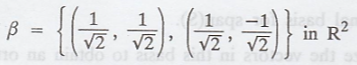
The lengths of the
vectors in β are,
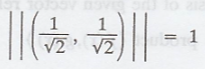
and
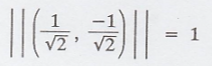
It is also given that
the vectors 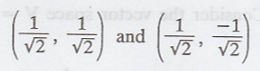 are linearly independent.
are linearly independent.
Hence, β is an
orthonormal basis of R2.
If β is an orthnormal
subset of an inner product space V and let x Є V, then define the Fourier
coefficients of x relatives to β to the scalars (x,y), where y Є β.
.'. Fourier
coefficients of (3, 4) are,
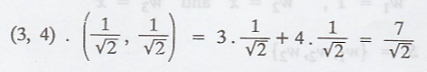
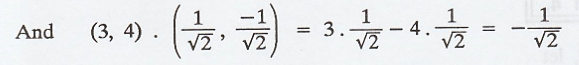
.'. The required
Fourier coefficients of (3, 4) are and 7/√2 and -1/√2
Problem 5.
Apply the Gram-Schmidt
process to the given subset S the inner product space V to obtain
(a) Orthogonal basis
for span(S).
(b) Normalize the
vectors in this basis to obtain an orthonormal basis β for span(S).
(c) Compute the Fourier
co-efficiensis of the given vector relative to β.
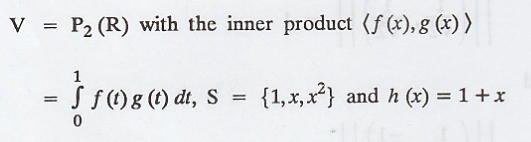
Solution:
Consider the vector
space V = P2(R) with inner product defined as,
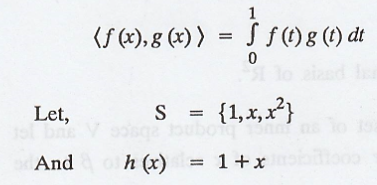
Let the vectors,
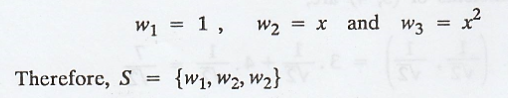
(a) Now, apply
Grass-Schmidt process
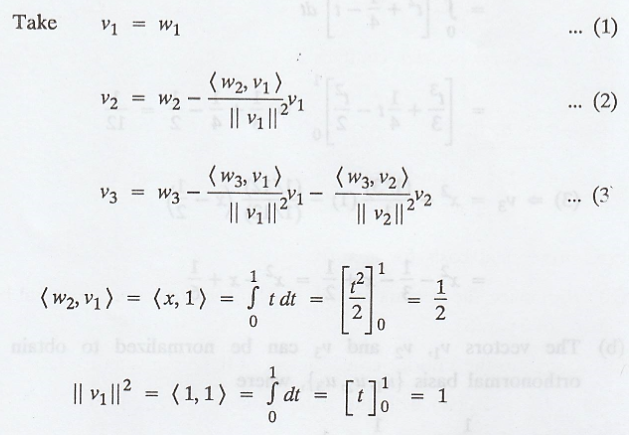
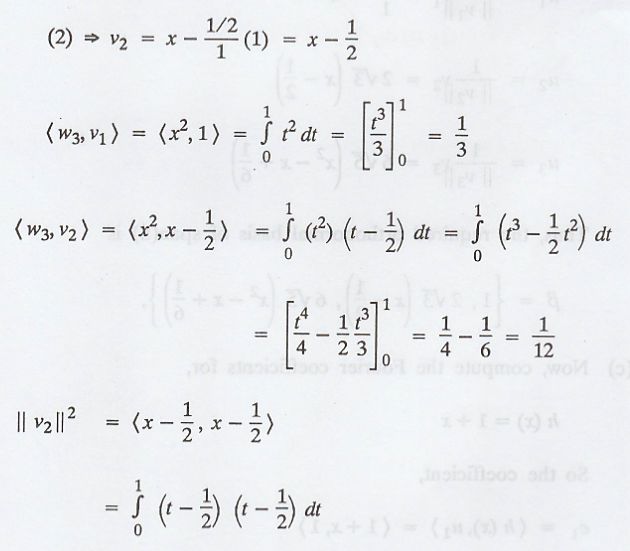
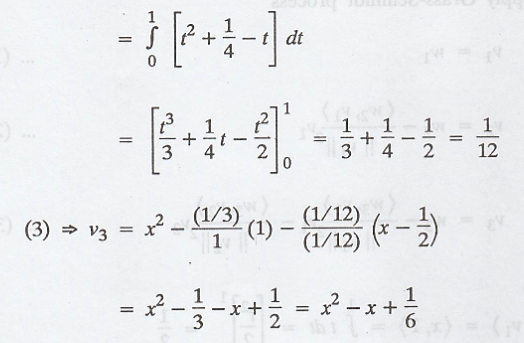
(b) The vectors v1,
v2 and v3 can be normalized to obtain the orthonormal
basis {u1, u2, u3}, where
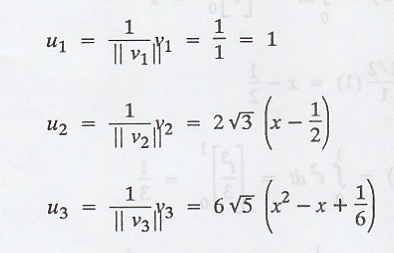
Thus, the required
orthonormal basis of span(S) is
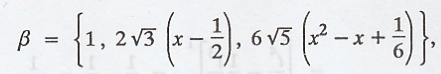
(c) Now, compute the
Fourier coefficients for,
h(x) = 1 + x
So the coefficient,
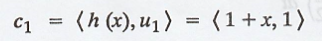
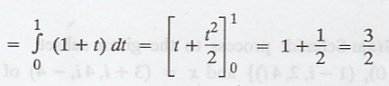
Again,
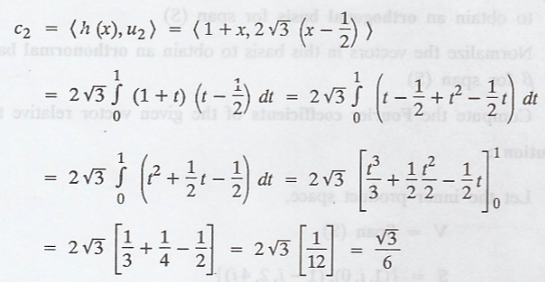
And,
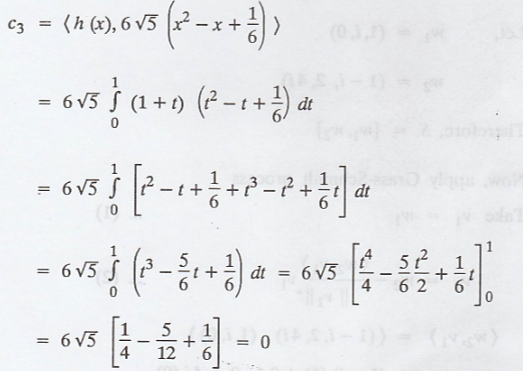
Hence, the required
Fourier coefficients are
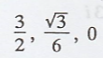
Problem 6.
Apply the Gram-Schmidt
process to the given subset
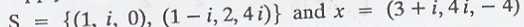 of the inner
product space V = R3
of the inner
product space V = R3
(a) to obtain an
orthogonal basis for span (S)
(b) Normalize the
vectors in this basis to obtain an orthonormal basis β for span (S)
(c) Compute the Fourier
coefficients of the given vector relative to β.
Solution
:
Let the inner product
space,
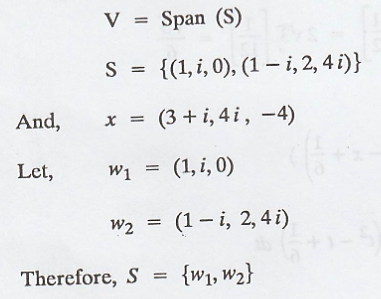
(a) Now, apply
Grass-Schmidt process
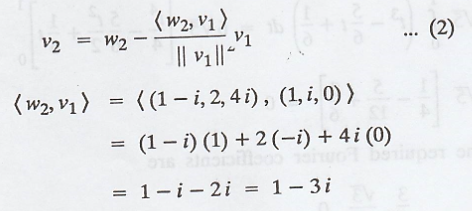
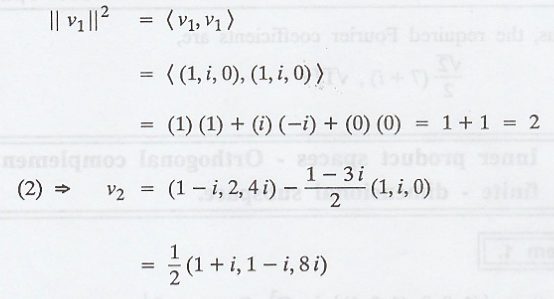
(b) The vectors v1
and v2 can be normalized to obtain the orthonormal basis {u1,
u2} where,
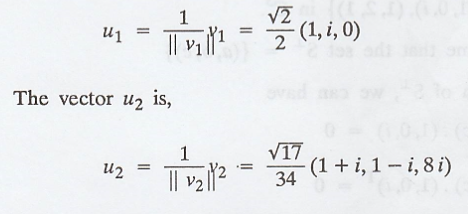
(c) Next compute the
Fourier coefficients for,
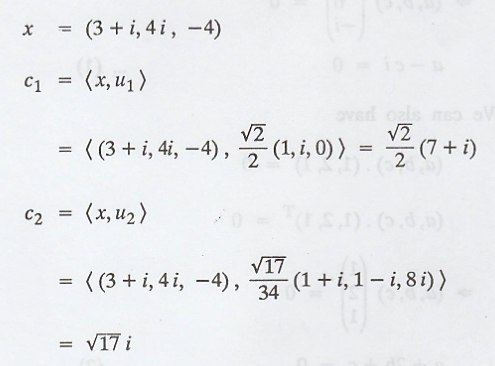
Thus, the required
Fourier coefficients are,
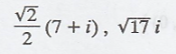
Random Process and Linear Algebra: Unit V: Linear Transformation and Inner Product Spaces,, : Tag: : - Inner Product spaces Orthogonal sets R2, R3, R4, C4, P(R)
Related Topics
Related Subjects
Random Process and Linear Algebra
MA3355 - M3 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
