Random Process and Linear Algebra: Unit V: Linear Transformation and Inner Product Spaces,,
Inner Product Spaces
In this chapter we shall study the vector spaces over a field of reals or a field of complex numbers. For vector space over these fields we shall introduce an idea of the length of a vector and when the field is of real numbers, we shall also be able to introduce an idea of the angle between two vectors. After that we shall see that lengths and angles may be expressed interms of a certain type of scalar valued function which is called an inner product.
INNER PRODUCT
SPACES
Introduction :
In this chapter we
shall study the vector spaces over a field of reals or a field of complex
numbers. For vector space over these fields we shall introduce an idea of the
length of a vector and when the field is of real numbers, we shall also be able
to introduce an idea of the angle between two vectors. After that we shall see
that lengths and angles may be expressed interms of a certain type of scalar
valued function which is called an inner product.
Many geometric notions
such as angle, length, and perpendicularity in R2 and R3
may be extended to more general real and complex vector spaces. All of these
ideas are related to the concept of inner product.
INNER
PRODUCTS AND NORMS
(a) Inner
Product spaces:
Definition :
Let V be a vector space
over F. An inner product on V is a function that assigns, to every ordered pair
of vectors x and y in V, a scalar in F, denoted <x,y>, such that for all
x, y and z in V and all c in F, the following axioms hold.

(d) <x,x> > 0
if x ≠ 0
Note that (c) reduces
to <x,y> = <y, x> if F = R. Conditions (a) and (b) simply require
that the inner product be linear in the first component.
It is easily shown that
if a1, a2, ..., an Є F and y, v1, v2,
..., vn Є V, then
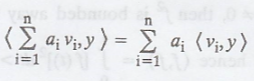
Note:
Standard inner product is usually called the dot product and is denoted by
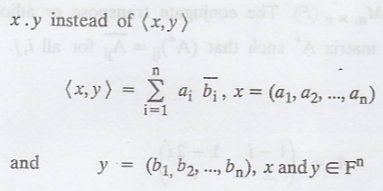
Example 1.
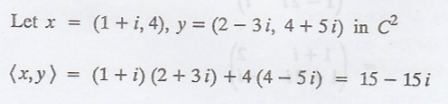
Example 2.
If <x,y> is any
inner product on a vector space V and r> 0, we may define another inner
product by the rule <x,y>' = r <x,y>.
If r ≤ 0, then (d)
would not hold.
Example 3.
Let V = C([0, 1]), the
vector space of real-valued continuous functions on [0, 1].
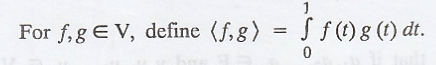
Since the preceding
integral is linear in f, (a) and (b) are immediate, and (c) is trivial. If f ≠
0, then f2 is bounded away from zero on some subinterval [0, 1] and
hence 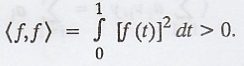
Definition :
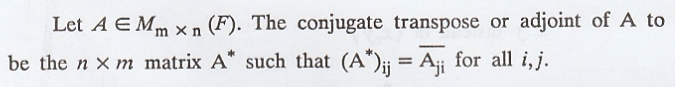
Example 4.
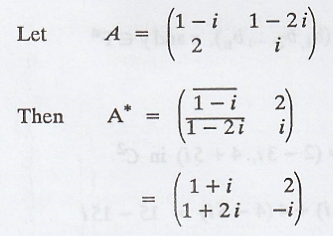
Note: If
x and y are viewed as column vectors in Fn, then <x,y> = y*x.
In the case that A has
real entries, A* is simply the transpose of A.
Example 5.
Frobenius inner
product
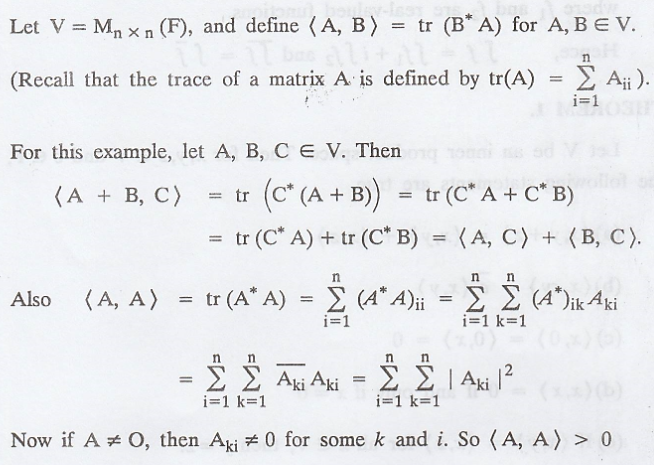
Note :
1. A vector space V
over F endowed with a specific inner product is called an inner product space.
2. If F = C, we call V
a complex inner product space, whereas if F = R, we call V a real inner product
space.
3. It is clear that if
V has an inner product <x, y> and W is a subspace of V, then W is also an
inner product space when the same function <x,y> is restricted to the
vectors x, y Є W.
4. A very important
inner product space that resembles C([0, 1]) is the space H of continuous
complex-valued functions defined on the interval [0, 2π] with the inner product
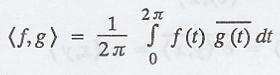
The reason for the
constant 1/2π will become evident later.
5. Every complex-valued
function f may be written as f = f1 + i f2, where f1
and f2 are real-valued functions.
Hence, 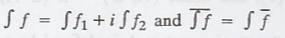
THEOREM 1.
Let V be an inner
product space. Then for x, y, z Є V and C Є F, the following statements are
true.
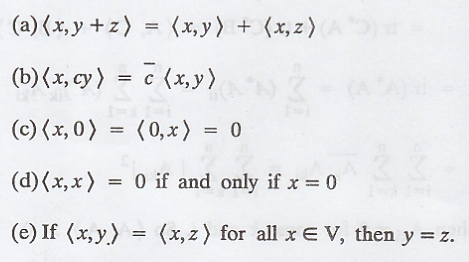
Proof :

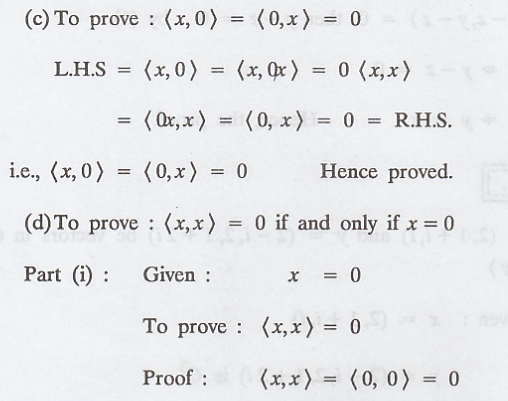
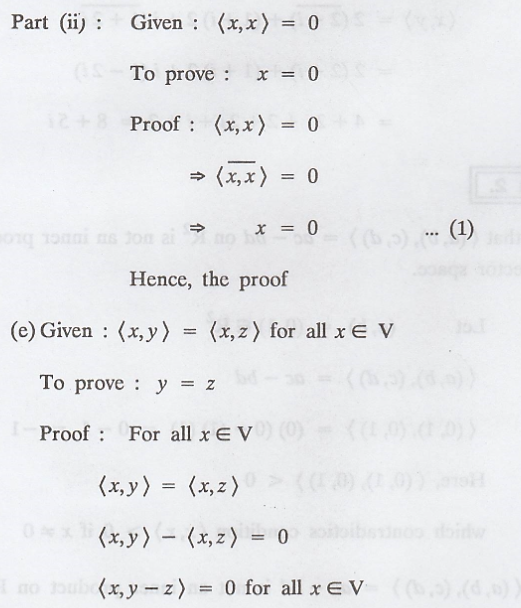
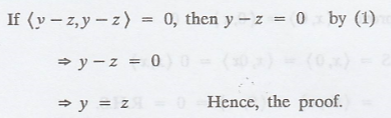
Problem 1.
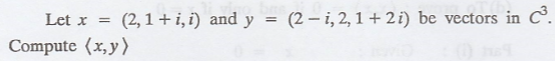
Solution
:
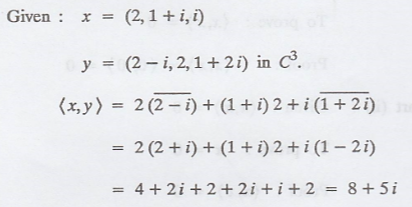
Problem 2.
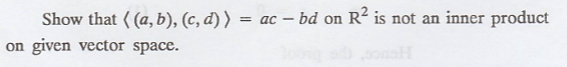
Solution
:
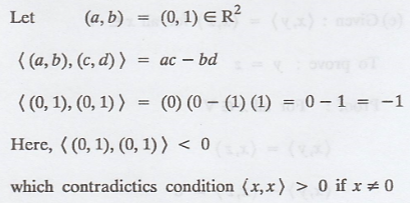
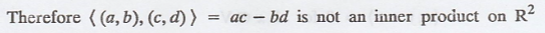
Problem 3.
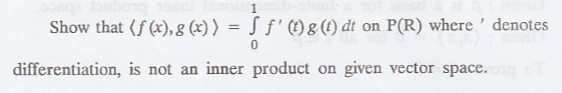
Solution
:
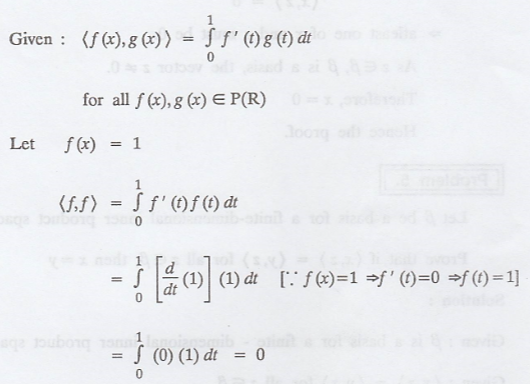
which is a
contradiction to the condition
<x, x> > 0 if
x ≠ 0
.'. Given is not an
inner product on P(R)
Problem 4.
Let β be a basis for a
finite-dimensional inner product space.
Prove that if <x, z>
= 0 for all z Є β, then x = 0
Solution
:

Problem 5.

Solution
:

Proof :
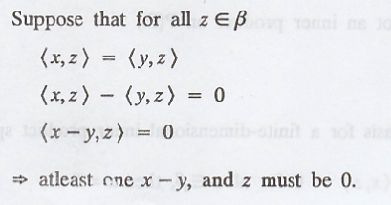
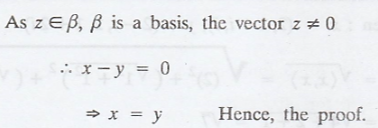
Random Process and Linear Algebra: Unit V: Linear Transformation and Inner Product Spaces,, : Tag: : - Inner Product Spaces
Related Topics
Related Subjects
Random Process and Linear Algebra
MA3355 - M3 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
