Random Process and Linear Algebra: Unit V: Linear Transformation and Inner Product Spaces,,
Inner product spaces - Orthogonal complement, Finite - Dimensional subspace
Problems about Inner product spaces - Orthogonal complement, Finite - Dimensional subspace
(c) Inner
product spaces - Orthogonal complement, finite - dimensional subspace.
Problem 1.
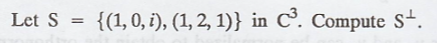
Solution
:

We can also have
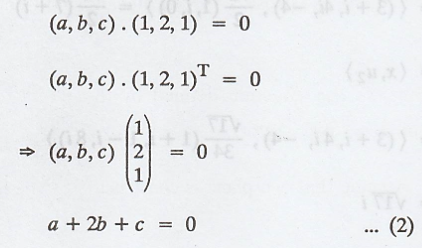

Therefore, we have the
solution set which is the required ![]() which can be given as :
which can be given as :
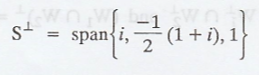
Problem 2.
Let S0 = {x0},
where x0 is a nonzero vector in R3. Describe ![]() geometrically.
Now suppose that S = {x1, x2} is a linearly independent
subset of R3. Describe
geometrically.
Now suppose that S = {x1, x2} is a linearly independent
subset of R3. Describe ![]() geometrically.
geometrically.
Solution
:
Let S0 = {x0},
where x0 is a nonzero vector in R3.
Assume x0 as
a direction.
Therefore, by
definition, ![]() consists of two linearly independent vectors.
consists of two linearly independent vectors.
A plane, orthogonal to
the direction defined by the vector x0, is constructed by span of
these two vectors.
Let S = {x1,x2}.
Assume that one plane is constructed by spanning of the vectors contained in S.
Therefore, by
definition, ![]() consists of a single element. A linear span of this element is
a line.
consists of a single element. A linear span of this element is
a line.
Therefore, ![]() represents a line orthogonal to the plane which can be generated by the linear
span of the elements of S.
represents a line orthogonal to the plane which can be generated by the linear
span of the elements of S.
Problem 3.
Let W1 and W2
be subspaces of a finite-dimensional inner product space.
Prove that 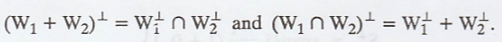
Solution
:
Let W1 and W2
be subspaces of a finite-dimensional inner product space.
To prove that
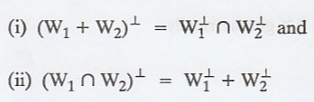
Proof :
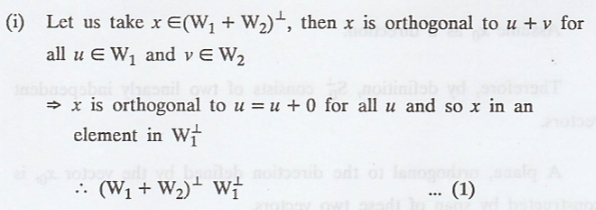
Proceeding in a similar
way, we can find that x is an element in ![]() and therefore,
and therefore,
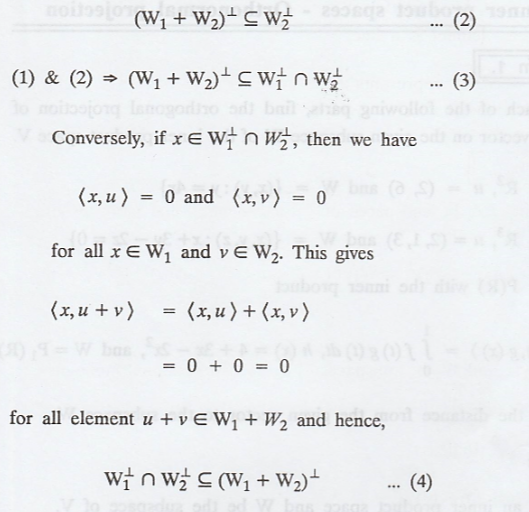
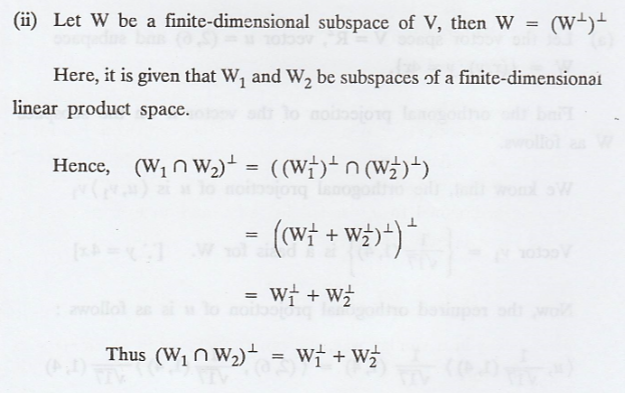
Random Process and Linear Algebra: Unit V: Linear Transformation and Inner Product Spaces,, : Tag: : - Inner product spaces - Orthogonal complement, Finite - Dimensional subspace
Related Topics
Related Subjects
Random Process and Linear Algebra
MA3355 - M3 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
