Random Process and Linear Algebra: Unit V: Linear Transformation and Inner Product Spaces,,
Inner Product space-Matrices
Problems under Inner product space - Matrices
(a) Inner
product space - Matrices
Problem 1.
Apply the Gram-Schmidt
process to the given subset S of the inner product space V to obtain
(a) Orthogonal basis
for span(S).
(b) Normalize the
vectors in this basis to obtain an orthonormal basis β for span(S).
(c) Compute the Fourier
co-efficiensis of the given vector relative to β.
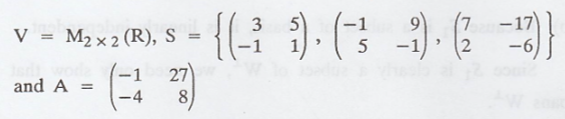
Solution
:

(a) Now apply
Gram-Schmidt process
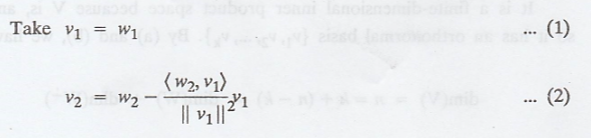
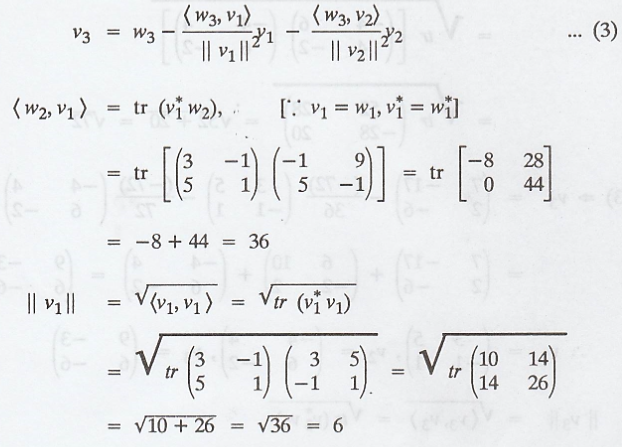
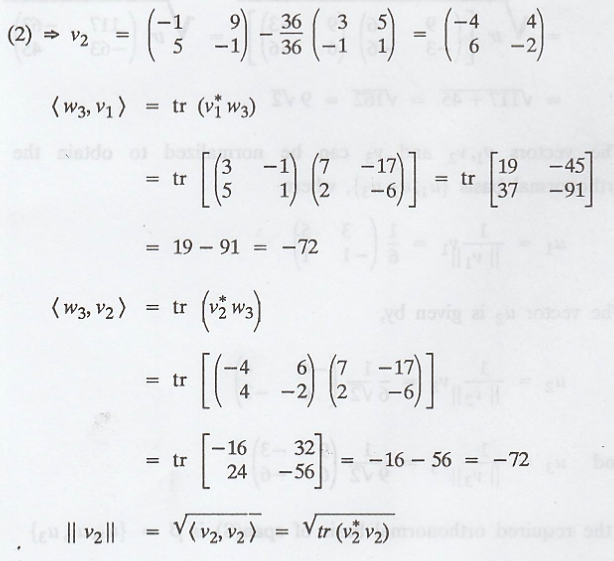

(b) The vectors v1,
v2 and v3 can be normalized to obtain the orthonormal
basis {u1, u2, u3}, where
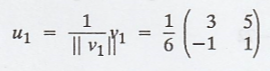
The vector u2
is given by,
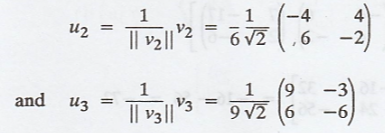
Thus, the required
orthonormal basis of span(S) is β = {u1, u2, u3}
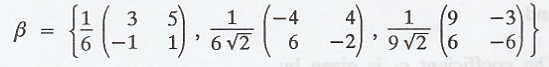
[Use your calculator
for matrix multiplication]
(c) Next compute the
Fourier coefficients for,
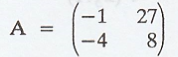
The coefficient c1
is given by
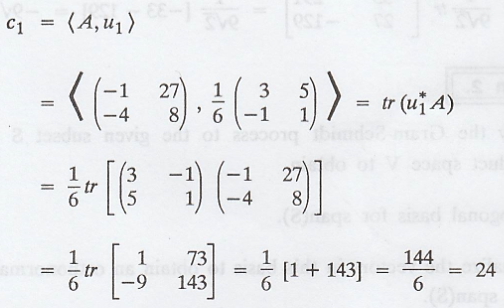
The coefficient c2
is given by

and
The coefficient c3
is given by
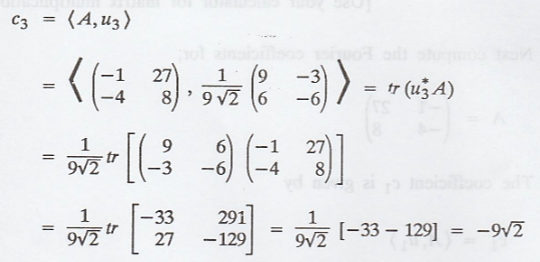
Problem 2.
Apply the Gram-Schmidt
process to the given subset S of the inner product space V to obtain
(a) Orthogonal basis
for span(S).
(b) Normalize the
vectors in this basis to obtain an orthonormal basis β for span(S).
(c) Compute the Fourier
co-efficiensis of the given vector relative to β.

Solution:

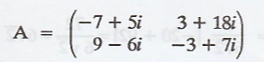

(a) Now apply
Gram-Schmidt process
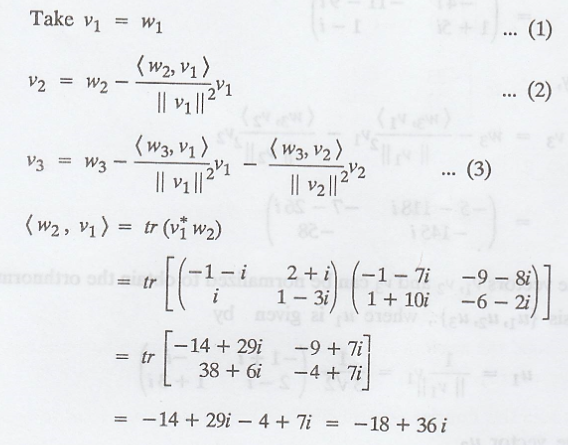
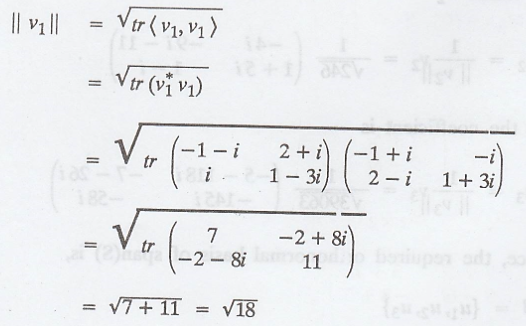
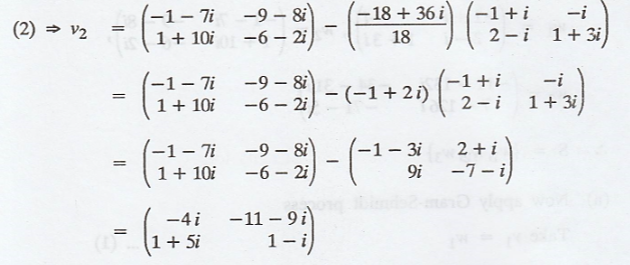

(b) The vectors v1,
v2 and v3 can be normalized to obtain the orthnormal
basis {u1, u2, u3}., where u1 is
given by
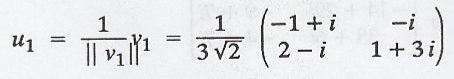
The vector u2
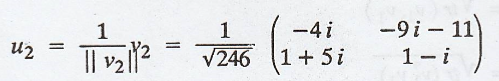
And the coefficient is

Hence, the required
orthonormal basis of span(S) is,
β = {u1, u2,
u3}

(c) Next compute the
Fourier coefficients for,

The coefficient c1
is,
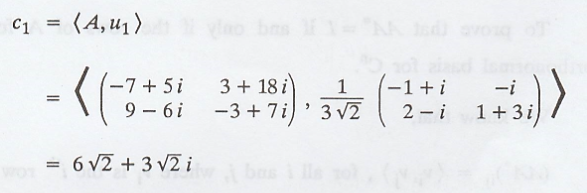
Again coefficient c2
is,
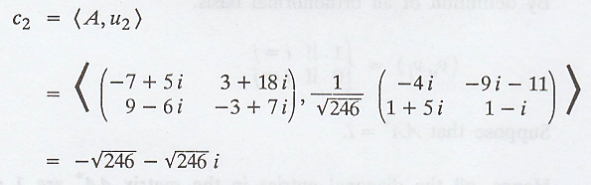
And,
The coefficient c3
is,
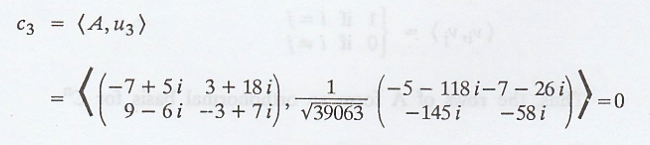
Thus the required
Fourier coefficients are

Problem 3.
Let A be an n x n
matrix with complex entries. Prove that AA* = I if and only if the rows of A
form an orthonormal basis for Cn.
Solution
:
Let A be an n X n
matrix with complex entries.
To prove that AA* = I
if and only if the rows of A form an orthonormal basis for Cn.
We know that,
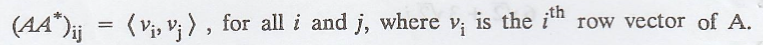
By definition of an
orthonormal basis.

Suppose that AA* = I.
Hence, all the diagonal
entries in the matrix AA* are 1 and all non-diagonal entries are 0.
Therefore, the entries
in AA* can be written as,
Thus, the rows of A form an orthonormal basis for Cn
Suppose the rows of A
form an orthonormal basis for Cn
Then,
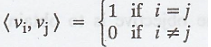
Observe that the
entries for the matrix AA* are either 0 or 1.
From the above
definition of <vi, vj>, observe that all the
diagonal entries in the matrix AA* are 1 and all non-diagonal entries are 0.
Thus, AA* = I
Problem 4.
Prove that for any
matrix 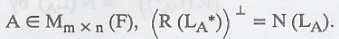
Solution
:
To prove that for any matrix 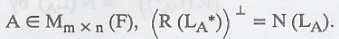
Suppose 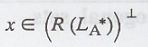
This gives that x is
orthogonal to A*y for all y Є Fm n
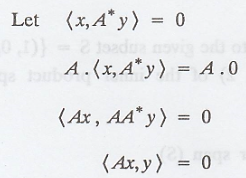
The above relation
holds for all y.
Therefore, Ax = 0

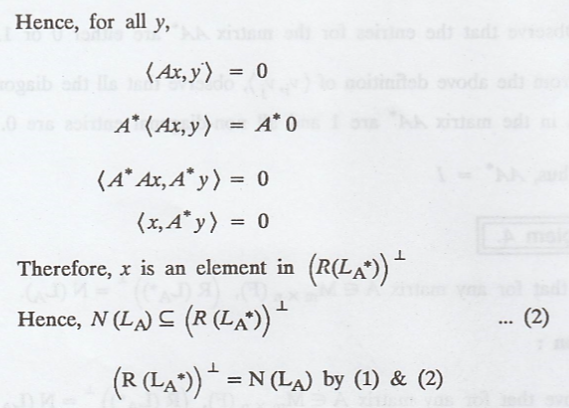
Random Process and Linear Algebra: Unit V: Linear Transformation and Inner Product Spaces,, : Tag: : - Inner Product space-Matrices
Related Topics
Related Subjects
Random Process and Linear Algebra
MA3355 - M3 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
