Impulse Response

IMPULSE RESPONSE

Properties of systems:

(i) Dynamicity (Memoryless systems)

Consider linear convolution,

The system is said to be static or memory less if present output depends only on present input. In the above equation y(t) will depend x(t) only when t = 0. This means h(τ) is evaluated only at τ = 0 .i.e.,

h(τ) = 0 for τ ≠ 0

The above condition is true only for

h(τ) = Cδ(τ)

The system is memoryless or static if,

h(τ) = Cδ(τ)

If the above condition is not satisfied, the system will be dynamic.

(ii) Causality

Consider the convolution equation,

We know that the system is said to be causal if its output depends on present and past inputs. In the above equation,

x(t) is present inpat

x(t - τ) are past inputs for τ ≥ 0

and x(t - τ) are future inputs for τ < 0

The result of convolution must be zero for future inputs (i.e τ < 0) if the system is causal, x(t-τ) cannot be zero since it represents future inputs. Hence h(τ) must be zero for τ < 0 for the system to be causal i.e.,

For LTI system to be causal

Causality: h(τ) = 0 for t<0

This condition shows that an impulse response of a causal system is also causal.

(iii) Stability:

Consider the convolution equation,

The magnitude of the output will be

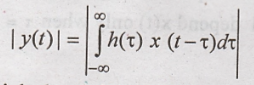
The right hand side of above equation can be written as,

The system is stable if it produces bounded input. Hence for x(t) to be bounded,

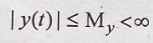
Using the above condition, we can write equation as

The system is stable if bounded output as given above is produced for bounded input. Hence for x(t) to be bounded,

If x(t - τ) is bounded then its maximum value will be M_x. Putting value in equation

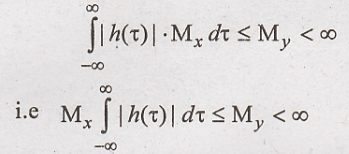
In the above equation M_x and M_y are maximum values of x(t) and y(t) respectively. Then for the above equation to be satisfied.

The above condition shows that the BIBO stable system has absolutely integrable impulse response.

(iv) Step Response

Consider the convolution equation,

Then equation can be writtern as,

Thus the step response becomes,

Step response = 

Here note that step response is the integration of impulse response.

Problem 1:

Check whether the following systems are stable and causal.

Solution:

Causality

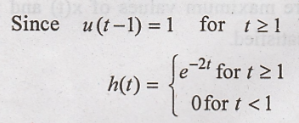
Since h(t) = 0 for t < 0 system is causal.

Stabilitiy

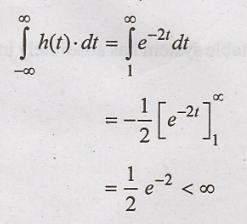
Since 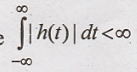, the system is stable

(ii) 

Causality:

Stability:

The system is stable.

(iii) 

Causality

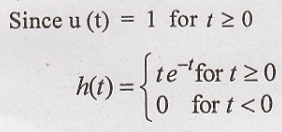
Therefore the system is causal.

Stability:

Hence the system is stable

Problem 2:

Verify whether the following systems are BIBO stable or not.

Solution:

This is causal system since

h(t) = 0 for t < 0

For stability,

Hence this system is stable

(ii) 

This is causal system since

h(t) = 0 for t < 0

For stability,

Hence the above equation becomes,

The value of cosine function is always from -1 to 1

Hence = 

Therefore this is stable system

Problem 3:

Determine the response of the system with impulse response h(t) = u(t) for the input x(t) = e^−2t .u(t)

Solution:

Given h(t) = u(t)

x(t) = e^−2t .u(t)

Output of the system is given by the convolution integral as,

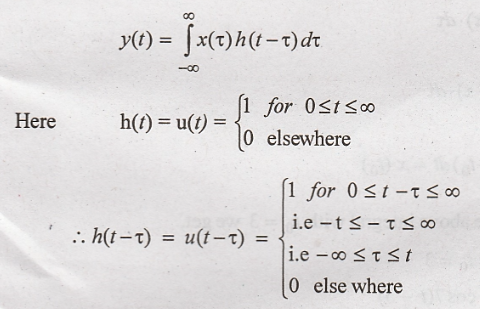
Putting above expression in convolution equation:

Now x(t) = e^-2t .u(τ), hence above equation will be,

Since u(τ) = 1 for 0 ≤ τ ≤ ∞, above equation will be,

Problem 4:

Find the output of an LTI with impulse response h(t) = δ(t - 3) for the input x(t) = cos 4t + cos7t.

Solution:

Here, h(t) = δ(t - 3) and

x(t) = cos 4t + cos 7t

Output of the system is given by convolution integral as,

By shifting property 

Using this property to solve above integral with t₀ = 3 we get,

Problem 5:

Find the response of the system shown in figure 3.21 for the output x(t) = δ(t)-δ(t-1.5). Here h(t) is impulse of the system.

Solution:

The impulse response of the system is given as,

y(t) = x(t)* h(t) = δ(t)* h(t) - δ(t-1.5)* h(t)

By replication property of impulse function, first convolution will be h(t),

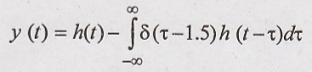
For above integration, use shifting property of impulse function, 

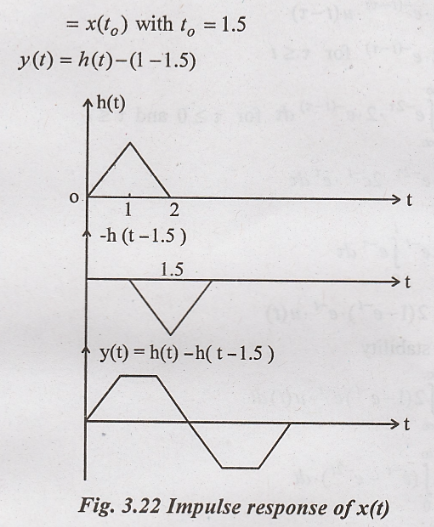
Problem 6:

The system shown below is formed by connecting two systems in cascade. The impulse response of the system are given by h₁(t) and h₂(t) . Find the over all impulse response of the system and determine if the system is BIBO stable.

Solution:

To obtain over all impulse response for cascade connection,

To check BIBO stability

Problem 7:

Find the step response of the system whose impulse response is given as h(t) = u(t+1) - u(t-1)

Solution:

Taking Laplace transform of given impulse response,

We know that . Taking inverse Laplace transform of the above equation