Signals and Systems: Unit III: Linear Time Invariant Continuous Time Systems,,
Important 2 marks Questions with Answers of Linear Time Invariant-Continuous Time Systems
Anna university questions with answers
Important 2 mark questions with answers of Linear time invariant-continuous time systems. Anna university questions with answers
Important
2 Mark Questions with Answers
UNIT
3: LINEAR TIME INVARIANT-CONTINUOUS TIME SYSTEMS
1. Define impulse
response of a continuous time system.
Impulse response is the
output produced by the system when input is applied to the system. Impulse
response is denoted by h(t).
Impulse response is
obtained by taking inverse Fourier transform (or) Inverse Laplace transform of
transfer function.
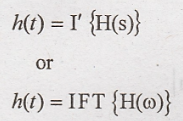
2. Write does the
input-output relation of LTI system in time and frequency domain.
In time domain : y(t) =
y(t) * x(t)

3. Find the impulse
response of the given system. y(t) = x(t – t0)
Take Laplace transform
of given equation.
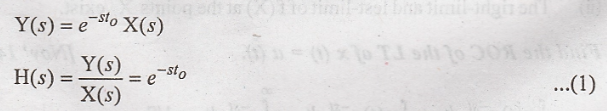
Taking inverse Laplace
transform of (1)
h(t) = δ(t-t0)
4. Define transfer function
in CT systems.
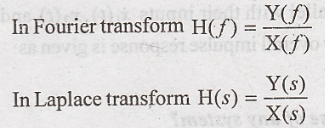
Transfer function
relates the transforms of input and output.
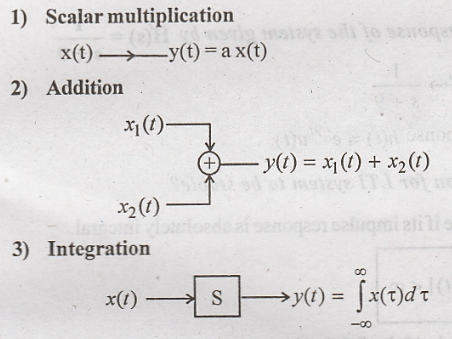
5. What are the three
elementary operations in block diagram representation of continuous time
system.
The three elementary operations in block diagram representation of continuous time system are,
6. Find the transfer
function of LTI system described the differential equation.
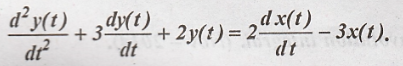
Taking Fourier
transform of given differential equation.
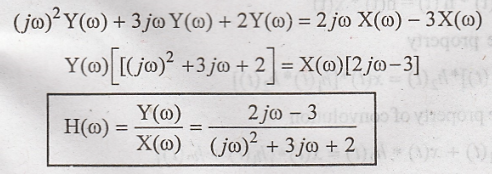
7. What is the impulse
response of two LTI systems connected in parallel?
If two systems are connected in parallel with their inputs x1(t), x2(t) and their impulse response h1(t) and h2(t) then their overall impulse response is given as
h(t) = h1(t)
+ h2(t).
8. What is meant by
impulse response of any system?
When the input x(t) is
applied to the system, then the output (response) of the system to the input is
known as impulse response.

The impulse response is
used to study the various properties such as system stability, dynamicity,
causality etc.
9. Find the impulse
response of the system given by 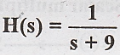
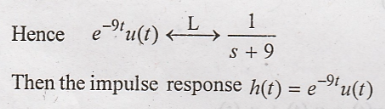
10. What is the
condition for LTI system to be stable?
An LTI system is stable
if its impulse response is absolutely integral.
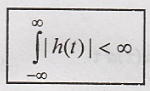
An LTI system is stable
if the ROC of its system transfer function includes
Re(s) = 0 (jω of S
plane).
11. List the properties
of convolution integral. (Nov - 2014).
(1) Commutative
property
y(t) = x(t) * h(t) =
h(t) * x(t)
(2) Associative
property
[x(t) * h1(t)]
* h2(t) = x(t) * [h1(t) * h2(t)]
(3) Distributive
property of convolution
x(t) * h1(t)
+ x(t) * h2(t) = x(t) * {h1(t) + h2(t)}
12) State the
significance of impulse response (Nov - 2014)
Impulse response is
used to analyze the properties of a system such as dynamicity, equality and
stability. Impulse response is a response of impulse δ(t) to any system.
13) Find the transfer
function for the system described by the difference equation 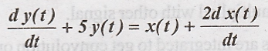 (Apr/May 2008)
(Apr/May 2008)
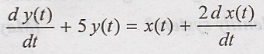
Take fourier transform
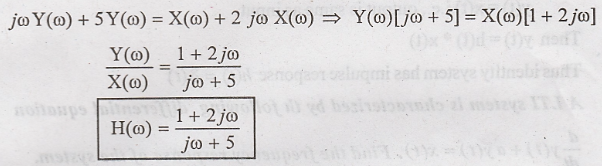
14) State the
condition for LTI system to be causal and stable.
For a LTI system to be
causal,
Causality: h(t) = 0 for
t < 0
This condition shows
that an impulse response of a causal system is also causal. Stability:
A LIT system is stable
if, Stability: 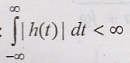
This condition show
that the BIBO stable system has absolutely integrable impulse response.
15) Differentiate
between natural response and forced response. (Nov/Dec: 2015)
i. In natural response
only initial conditions are considered and input is zero.
ii. The forced response
of the system is obtained only for input, with zero initial conditions.
16) Check whether the
causal system with transfer function H(s) = 1/S-2 is stable. (Dec-13)
The pole lies at s = 2.
Since the pole of causal system does not lie on left side of jω axis, the
system is not stable.
17) What are the basic
steps involved in convolution integrals?
Folding
:
One of the signal is first folded at t = 0.
Shifting
:
The folded signal is shifted right (or) left depending upon time at which
output is to be calculated.
Multiplication:
The shifted signal is multiplied with other signal.
Integtation
:
The multiplied signals are integrated to get convolution output.
18) What is the impulse
response of an identity system? (May 08)
For an identity system.
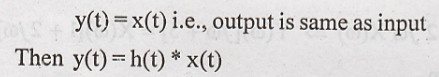
Thus identity system
has impulse response h(t) = δ(t)
19. A LTI system is
characterized by th following differential equation 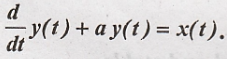 Find the
frequency response of the system.
Find the
frequency response of the system.
Taking fourier
transform of given differential equation.
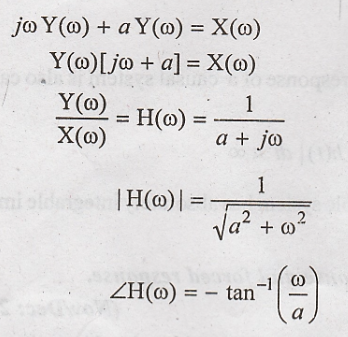
20) Write the Nth
order differential equation.
The Nth
order differential equation can be written as
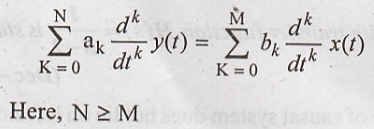
21) Define the
frequency response of the CT system. [Nov-11]
The response of a CT
system to a complex sinusoidal signal gives the frequency response of the CT
system.
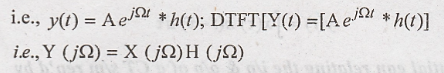
Here, H(jΩ) is the
frequency response of the CT system
22) Check the causality
of the system with impulse response h(t) = e-t u(t). [Nov-12]
For an LTI-CT system to
be causal, h(t) = 0 for t < 0.
Here, h(t) = e-t
u(t) = 0 for t < 0. Hence, causal system
23) Draw the block diagram
of the LTI system 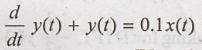 [Nov-14] (R13)
[Nov-14] (R13)
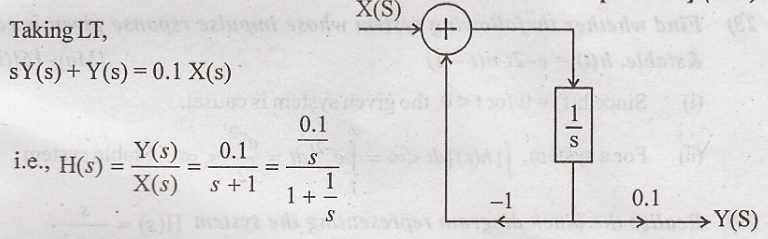
24) What is u(t-2) *
δ(t-1)? [Nov-15] (R13)
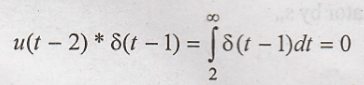
25) Give the
differential equation representation of a system 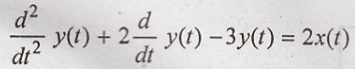 . Find the frequency
response H(jΩ) [Nov-15] (R13)
. Find the frequency
response H(jΩ) [Nov-15] (R13)
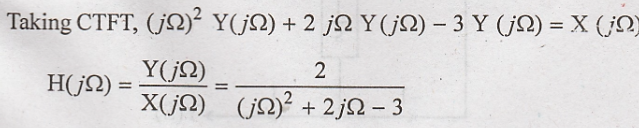
26) Define Convolution
integral of CT systems.
The convolution
integral gives the output or response of a CT system which is the convolution
of the input sequence [x(t)] & Impulse response [h(t)] sequence.
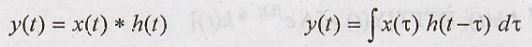
27) Find the
differential eqn relating the i/p & o/p of a CT s/m rep'd by 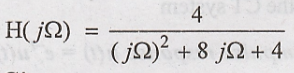 [May-14]
[May-14]
Given:
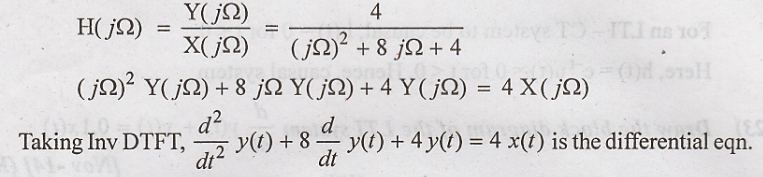
28) Find whether the following
system whose impulse response given is causal & stable. h(t) = e-2t
u(t-1) [May-16](R13)
(i) Since h(t) = 0 for
t < 0, the given system is causal.
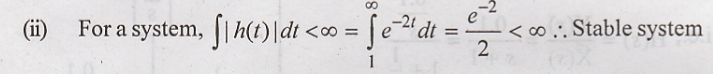
29) Realize the block
diagram representing the system H(s) = 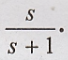
Divide Numerator &
Denominator by s,.
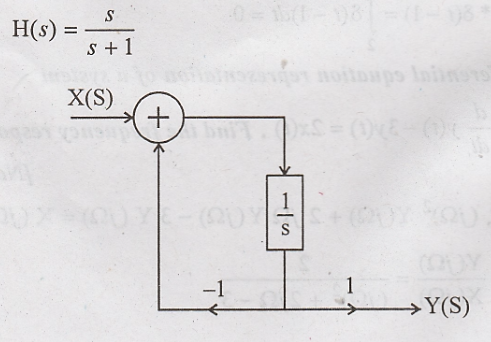
Signals and Systems: Unit III: Linear Time Invariant Continuous Time Systems,, : Tag: : Anna university questions with answers - Important 2 marks Questions with Answers of Linear Time Invariant-Continuous Time Systems
Related Topics
Related Subjects
Signals and Systems
EC3354 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
