Signals and Systems: Unit IV: Analysis of Discrete Time Signals,,
Important 2 marks Questions with Answers Analysis of Discrete Time Signals
Anna University Important 2 marks Questions with Answers Analysis of Discrete Time Signals
Important Two Marks Questions with Answers
UNIT 4: ANALYSIS OF
DISCRETE TIME SIGNALS
1.
Define z transform
z
transform of discrete time signal x(n) is defined as
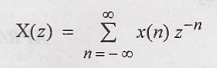
Here
z is complex variable. x(n) and x(z) is called z transform pair.
z
transform pair: 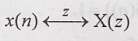
2.
State the relation between DTFT and z transform Nov/Dec 2015.
z
transform is given as
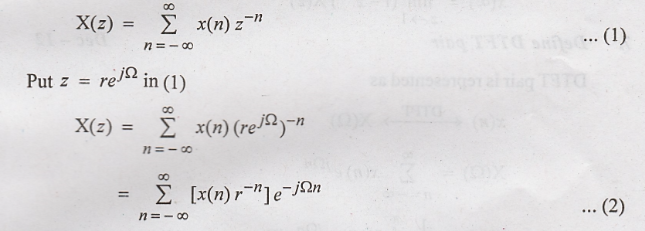
But
DTFT is given as
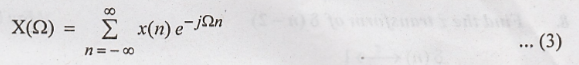
By
comparing X(z) and X(Ω), we find that X(z) indicates a Fourier transform of
x(n) r-n.
3.
List any two properties of region of convergence (ROC) in z domain APR/May 2008
(i) ROC of causal sequence (Right hand Sided sequence) is in the form of |z| > r.
(ii) ROC of non causal sequence (Left hand sided sequence is in the form of |z| < r.
4.
Obtain z transform of x(n) = {1, 2, 3, 4}
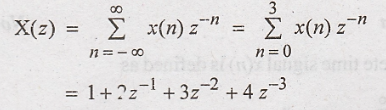
5.
What is z transform of A δ(n+ k)? APR/May 13.
By
time shifting property
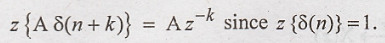
6.
State final value theorem of z transform. May - 12
The
final value of a sequence is given as
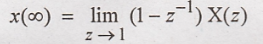
7.
Define DTFT pair Dec - 12
DTFT
pair is represented as
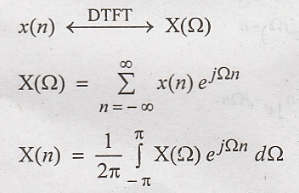
8.
Find the z transform of δ(n-2) May 07
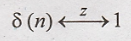
By
time shifting property 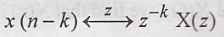

9.
What is the z transform of u(n) and δ(n)?
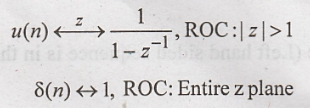
10.
What is aliasing? Nov/Dec 14.
When
the high frequency interferes with low frequency and appears as low frequency,
then this phenomenon is called aliasing.
11.
State the methods of find inverse z transform. May/99
Inverse
z transform can be obtained using
(i)
Power series expansion (ii) Partial fraction expansion (iii) Contour
integration.
12.
State the sampling theorem May/11
A
bandlimited signal of finite energy, which has no frequency components higher than
W hertz, is completely described by specifying the values of the signal at
instants of time separated by 1/2W seconds.
13.
What is meant by antialiasing filter? Dec / 09.
Analog
signal is passed through a lowpass filter before sampling takes place. This
lowpass filter bandlimits the analog signal. This lowpass filter eliminates the
aliasing effect. Hence it is known as anti aliasing filter.
14.
Consider the analog signal
x(t)
= 4 cos 100 πt + 15 sin 300 πt - 2 cos 100 πt Dec/11
x(t)
= 4 cos 100 πt + 15 sin 300 πt - 2 соs 100 πt compare this given equation with
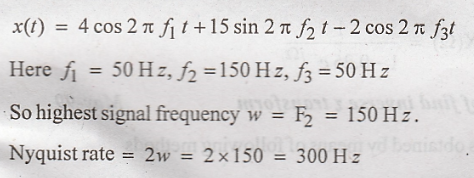
15.
Determine the z transform of x(n) = (n-3) u(n)
Solution:
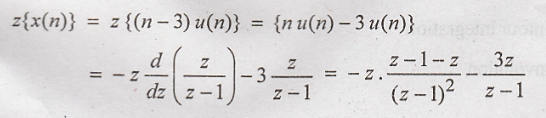
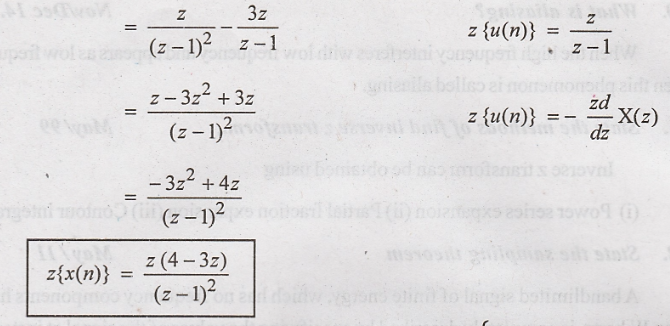
16.
Find the Fourier transform of the sequence x(n) = 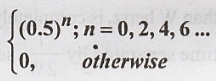
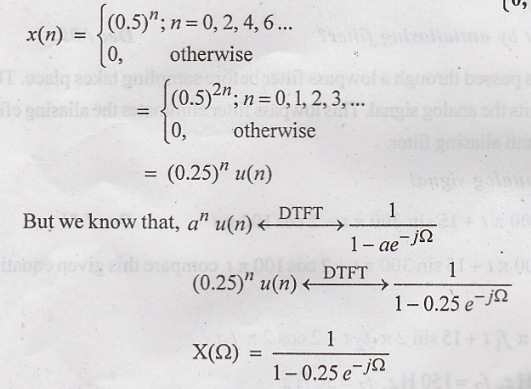
17. State the methods of find
inverse z transform May-99
Inverse
z transform is obtained by means of following methods
(i)
Power series expansion
(ii)
Partial fraction expansion
(iii)
Contour integration
(iv)
Convolution
18.
Determine the z transform of x(n) = δ(n) - 0.95 δ(n-6)
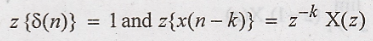
The
z transform of given function is
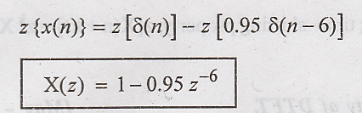
19.
What is the inverse z transform of 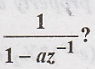
From
the standard z transform representation
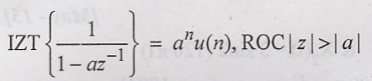
20.
State parseval's relation in a transform.
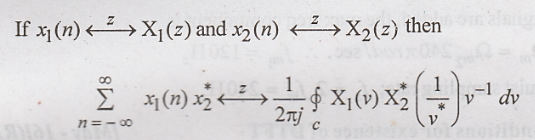
21.
State the Convolution property of Z-transform. [Nov - 12]
z[x(n)
* h(n)] = X(z) H(z) ... i.e., The Z-transform of the Convolution in the time
domain is equal to the product of their Z-transforms in the freq domain.
22)
Prove the Time-Shifting property of DTFT. [May-12]
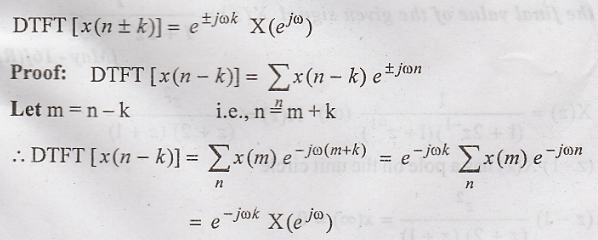
23)
State the Final value theorem. [May-12]
Final
value theorem: 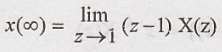
24)
What is the z-transform of δ(n + k) [May-13]
W.K.T,
z[δ(n) = X(z) = 1. Using time-shifting property, z[X(n+ k)] = zk
X(z)
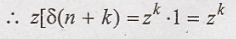
25)
State the multiplication property of DTFT. [May - 14]
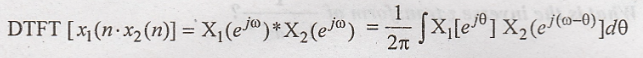
26)
Determine the Nyquist sampling rate for X(t) = sin (200πt) + 3 sin2 (120πt).
[May-15] (R13)
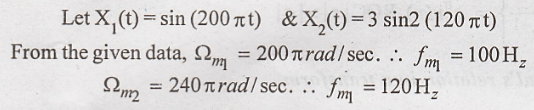
When
both signals are added, the max freq component is
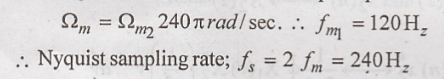
27) Write the conditions for
existence of DTFT [May-16](R13)
A
sufficient condition for the existence of DTFT for an a periodic sequence X(n)
is 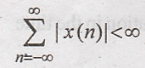 .i.e., if a sequence X(n) is absolutely summ able, then DTFT
exists for the sequence X(n).
.i.e., if a sequence X(n) is absolutely summ able, then DTFT
exists for the sequence X(n).
28)
Find the final value of the given signal X(z) = 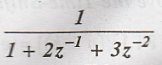 [May-16](R13)
[May-16](R13)
Given:
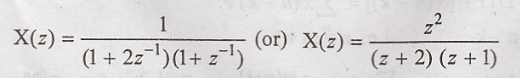
Here,
(z - 1) X(z) has a pole on the unit circle
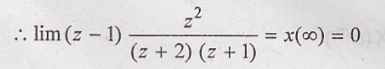
Signals and Systems: Unit IV: Analysis of Discrete Time Signals,, : Tag: : - Important 2 marks Questions with Answers Analysis of Discrete Time Signals
Related Topics
Related Subjects
Signals and Systems
EC3354 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
