Random Process and Linear Algebra: Unit III: Random Processes,,
Important 2 marks Questions and Answers of Random Process
Important Questions and Answers of Random Process
'2' Marks
Questions and Answers
1. Give an example for a continuous time random process. [A.U. N/D 2004, CBT A/M 2011]
2. Define a Stationary
process. [A.U. N/D 2004, CBT M/J 2010]
Solution:
A random process X(t)
is said to be stationary in tl strict sense if its statistical characteristics
do not change with time.
i.e., the random
processes X(t1) and X(t2) where t2 = t1
+ ∆ will have all statistical properties the same.
3. State the four types
of a stochastic processes. [A.U. A/M 2004] [A.U Trichy A/M 2010, CBT M/J 2010,
A/M 2019 R13 PQT, RP]
Solution:
(i) Discrete time,
discrete state random process.
(ii) Discrete time,
continuous state random process.
(iii) Continuous time,
discrete state random process.
(iv) Continuous time,
continuous state random process.
4. Prove that a first
order stationary random process has a constant mean. [A.U. Model] [A.U A/M
2011, N/D 2013]
Solution:
See Page No. 3.7
Theorem 1.
5.Define (a) wide sense
stationary random process, (b) ergodic random process. (or) When a random
process said to be Ergodic process? [A.U Trichy M/J 2011, M/J 2012, A/M 2017
(R8, R13)] [A.U. Model] [A.U N/D 2017 (RP) R13][A.U A/M 2019 R8 RP] [M/J 2013]
Solution:
(a) Wide sense
stationary random process :
A random process X(t)
is said to be wide sense stationary if its mean is constant and its
autocorrelation depends only on time difference.
i.e., (i) E (X (t)) =
constant. (ii) RXX (t,t+τ) = RXX (τ)
(b) Ergodic Random
Process : [A.U CBT A/M 2011, CBT N/D 2011] [A.U M/J 2013]
A random process X (t)
is called ergodic if its ensemble averages are equal to appropriate time
averages.
6. Give an example of
an ergodic process. [A.U. A/M 2004]
Solution
:
1. A Markov chain
finite state space.
2. A stochastic process
X(t) is. ergodic if its time average tends to the ensemble average as T → ∞
7. What is a Markov
chain? When can you say that a Markov Chain is homogeneous ? [A.U. N/D 2004,
N/D 2010] [A.U N/D 2015, R-13]
Solution
If, for all n,
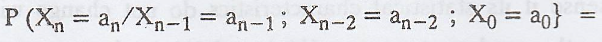
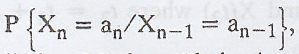 is
called a Markov Chain (a1, a2, ....an, are
called the states of the Markov Chain.
is
called a Markov Chain (a1, a2, ....an, are
called the states of the Markov Chain.
If Pij (n-1,
n) = Pij (m-1, m), the Markov chain is called a homogeneous Markov
chain.
8. Consider a Markov
chain with 2 states and transition probability matrix P = 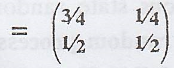 Find
the steady state probabilities of the chain. [A.U. Model]
Find
the steady state probabilities of the chain. [A.U. Model]
Solution:
Let the stationar,
probabilities of the chain be π = (π1
π2)
By the property of π, π
P = π
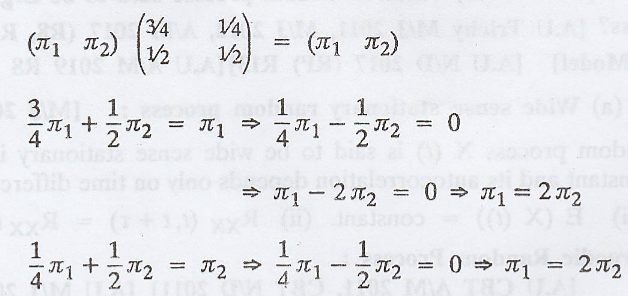
Since the above
equations are identical, consider this equation with π1 + π2
= 1
π1 = 2π2
.'. 3π2 = 1
=> π2 = 1/3 and π1 = 2/3
Hence the steady-state
probabilities of the chain is π = (π1 π2)
i.e., π = (2/3 1/3)
9. Define irreducible
Markov chain? And state Chapman Kolmogorow theorem. [A.U. N/D 2003]
Solution
:
If eeeeee for some n
and for all i & j, then every state can be reached from every other state.
When this condition is satisfied, the Markov chain is said to be irreducible.
The tpm of an irreducible chain is an irreducible matrix.
Chapman-Kolmogorov
theorem : [A.U A/M 2017 R-13]
If 'P' is the tpm of a
homogenous Markov chain, then the n-step tpm P(n) is equal to Pn

10. Define transition
probability matrix. [tpm] [AU N/D 2011]
Solution
:
The transition
probability matrix (tpm) of the process {xn, n ≥ 0} is defined by
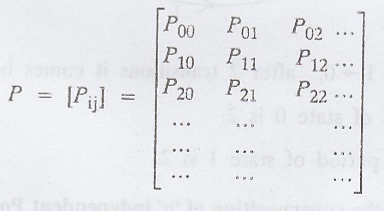
where the transition
probabilities (elements of P) satisfy Pij ≥ 0,
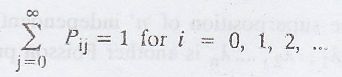
11. What is meant by
steady-state distribution of Markov chain? [A.U. A/M 2003] [A.U N/D 2017 R-08]
Solution:
If a homogeneous Markov
chain is regular, then every sequence of state probability distribution
approaches a unique fixed probability distribution called the stationary
(state) distribution or steady-state distribution of the Markov chain.
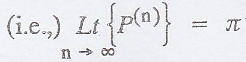 where the
state probability distribution at step n,
where the
state probability distribution at step n, 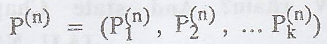 and the
stationary distribution at π = (π1, π2, ... πk)
are row vectors.
and the
stationary distribution at π = (π1, π2, ... πk)
are row vectors.
12. Consider a Markov
Chain with state {0, 1} and transition probability matrix eeeeee. Is the state
0 periodic? If so what is the period ? [A.U. A/M 2006]
Solution
:

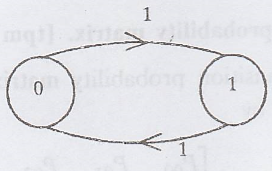
Starting from 0→1→0,
after 2 transitions it comes back to state 0.
Therefore, period of
state 0 is 2.
In the same way period
of state 1 is 2.
13. What will be the
superposition of 'n' independent Poisson processes with respective average
rates λ1, λ2, ... λn? [A.U. N/D 2004]
Solution:
The superposition of
'n' independent Poisson processes with average rates λ1, λ2,
… λn is another Poisson process with average rate λ1 + λ2
+ ... + λn
14. State any two
properties of a Poisson process. [A.U. A/M 2003] [A.U CBT A/M 2011, A.U N/D
2015 R-13 RP, A.U N/D 2017 R-13] [A.U. A/M 2018 R-13] [A.U N/D 2018 R13 PQT,
RP]
The Poisson process is
a Markov process:
(i) The Poisson process
possess the Markov property.
(ii) Sum of two
independent Poisson processes is a Poisson process.
(iii) Difference of two
independent Poisson processes is not a Poisson process.
15. State the
postulates of a Poisson process. [A.U. N/D 2003, A/M 2011, N/D 2017 (RP) R13,
N/D 2019 R17 PQT]
Solution:
Let X(t) = number of
times an event A say, occured upto time 't' so that the sequence {X(t), t ε [0,
∞)} forms a Poisson process with parameter 'λ'.
(i) Events occuring in
non-overlapping intervals are independent of each other.
(ii) P[X(t) = 1 for t
in (x, x + h)] = λh + 0(h)
(iii) P[X(t) = 0 for t
in (x, x + h)] = 1 - λh + 0(h)
(iv) P[X(t) = 2 or more
for t in (x, x + h)] = 0(h)
17. What do you man by
an absorbing Markov chain? Give an example.
Solution:
A state i of a Markov
chain is said to be an absorbing state if Pii = 1, i.e., if it is
impossible to leave it. A Markov chain is said to be absorbing if it has
atleast one absorbing state.
18. Write down the
relation satisfied by the steady-state distribution and the tpm of a regular
Markov chain.
Solution:
If π = (π1 π2
... πn) is the steady-state distribution of the chain whose tpm is
the nth order square matrix P, then πP = π
19. When is a Markov
chain completely specified?
Solution:
A Markov chain is
completely specified when the initial probability distribution and the tpm are
given.
20. What is a
Stochastic matrix? When is it said to be regular?
Solution:
In a square matrix the
sum of all the elements of each row is 1, is called a Stochastic matrix. A
stochastic matrix P is said to be regular if all the clements of pn
(for some positive integer n) are positive.
21. Check whether the
following matrix is stochastic? A = 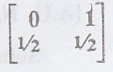 Is it a regular matrix?
Is it a regular matrix?
Solution
:
Definition:
Regular matrix : See
Page No. 3.90
Ist row sum
= 0 + 1 =1
IInd row sum
= 1/2 + 1/2 = 1
.'.The given matrix is
a stochastic.
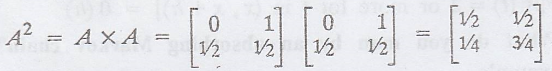
All the entries of A(2)
are positive.
.'. Given matrix A is
regular.
22. Is a Poisson process
a continuous time Markov Chain? Justify your answer. [A.U A/M. 2010]
Solution:
Yes.
By the property of
Poisson process, the conditional probability distribution of X(t3)
given all the past values X(t1) = n1, X(t2) =
n2 depends only on the most recent value X(t2) = n2.
i.e., The Poisson
process possesses the Markov property.
Poisson process with
Markov which take discrete values, whether t is discrete or continuous are
called Markov Chain.
Hence, Poisson process
is a continuous time Markov Chain.
23. What is meant by
one-step transition probability ?[A.U Trichy N/D 2010][A.U N/D 2017 R-13]
Solution:
The conditional
probability P[Xn = aj/Xn-1 = ai] is
called the one-step transition probability from state 'ai' to state
'aj' at the nth step and is denoted by Pij
(n-1, n)
24. Is Poisson process
stationary? Justify. [A.U A/M 2015 (R-13, R-8)][A.U N/D 2017 R-08]
Solution
:
Poisson process is not
a stationary process, as its statistical properties (mean, autocorrelation,
...) are time dependent.
25. What is a random
process? When do you say a random process is a random variable? [A.U A/M 2015
(R-13, R-8)]
Solution:
Random process is
function of the possible outcomes of an experiment and also time. i.e., X(s,
t).
It is fixed, then the
random process is a random variable.
26. Consider a Markov
chain with state {0, 1, 2} and transition probability matrix 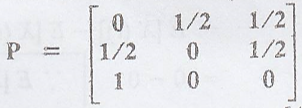 Draw
the state transition diagram. [A.U N/D 2015 R-8]
Draw
the state transition diagram. [A.U N/D 2015 R-8]
Solution
:
Given:


27. Give an example of
evolutionary random process. [A.U A/M 2015 (R-13, R-8)] [A.U N/D 2018 R13 RP]
Solution
:
Poisson process.
28. What is Markov
process? [AU N/D 2009] [A.U Tvli A/M 2009] [A.U M/J 2016 R13 RP, N/D 2019 R17
RP, A/M 2019 R17 RP] [A.U N/D 2019 R17 PQT]
Solution:
A random process X(t)
is said to be a Markov process if for any t1 < t2 <
t3 < ... < tn
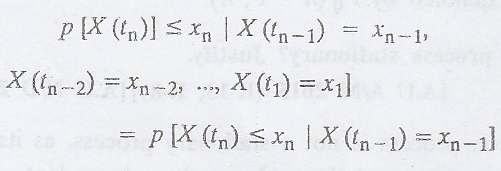
(i.e.,) the conditional
distribution of X(t) for given values of X(t1), X(t2)...
X(tn-1) depends only on X(tn-1)
29. Let X (t) be a
wide-sense stationary random process with slo E[X(t)] = 0 and Y(t) = X(t) - X(t
+ τ), τ > 0. Compute E[Y(t)] and Var[Y(t)] [A.U N/D 2019 R17 RP]
Solution:
Given: Y(t) = X(t) -
X(t + τ)
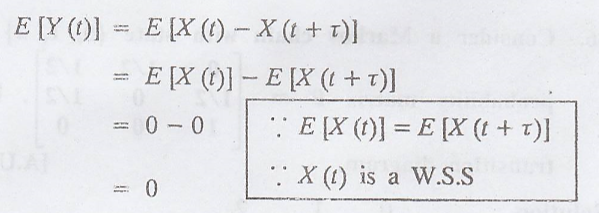

Random Process and Linear Algebra: Unit III: Random Processes,, : Tag: : - Important 2 marks Questions and Answers of Random Process
Related Topics
Related Subjects
Random Process and Linear Algebra
MA3355 - M3 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
