Signals and Systems: Unit III: Linear Time Invariant Continuous Time Systems,,
Fourier Transform Analysis of CT Systems
CT Systems, Frequency Response, Solution of Differential Equations, Problems Based on Fourier Transform Analysis of CT Systems
Discuss about CT Systems, Frequency Response, Solution of Differential Equations, Problems Based on Fourier Transform Analysis of CT Systems
FOURIES TRANSFORM ANALYSIS OF CT SYSTEMS
Fourier transform X(ω)
of signal x(t) gives the frequency spectrum of the signal.
i. Output of continuous
time system is represented as
y(t) = x(t) * h(t)
ii. By using
convolution theorem, the above equation becomes,
Y(ω) = X(ω).H(ω)
By taking inverse
Fourier transform of y(ω) we can obtain the output y(t) of the system.
Frequency Response
H(ω) is the frequency
response of LTI - CT system. It is also known as system
transfer function.
We know that, y(ω) =
X(ω).H(ω)
H(ω) = Y(ω)/X(ω)
Here Y(ω) ⇒ Fourier transform of
output y(t)
X(ω) ⇒ Fourier transform of
input x(t)
H(ω) ⇒ Fourier transform of
h(t) (i.e) impulse response.
Solution of Differential Equations
Consider the
differential equation
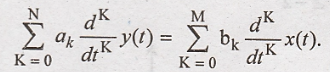
Apply differentiation
in time domain property of Fourier transform to above equation.
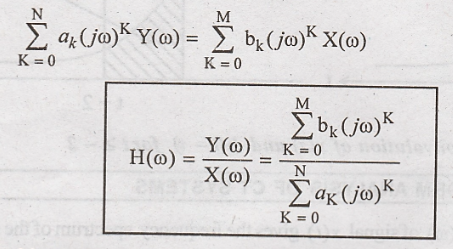
Problems Based on Fourier Transform Analysis of CT Systems
Problem 1:
Determine frequency
response and impulse response for the system described by the following
differential equation. Assume zero initial condition.
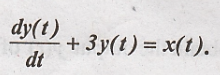
Solution:
(i) Frequency response
- H(ω)
Taking Fourier
transform of given differential equation.

(ii) Impulse Response
[h(t)]
Inverse Fourier
transform of H(ω) is h(t).

Taking Inverse Fourier
transform (1)
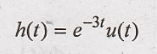
Problem 2:
The system produces the
output of y(t) = e-t u(t) for an input of x(t) = e-2t
u(t). Determine the impulse response and frequency response of the system. [May
13-Marks 16]
Solution:
(i) Frequency Response
- H(ω)

Taking Fourier
transform of (1)
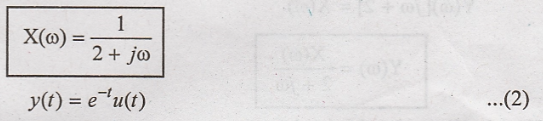
Taking Fourier
transform of (2)
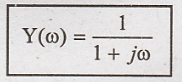
Frequency response H(ω)
= Y(ω)/X(ω)

(ii) Magnitude of
Frequency Response:
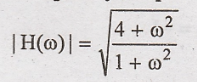
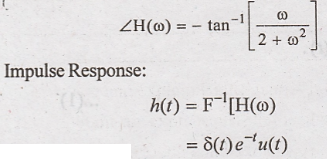
Problem 3:
Consider the continuous
time LTI system described by 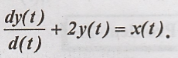
Obtain an output for
the input x(t) = e-t u(t) using fourier transform.
Solution:

Taking Fourier Transform
of (1)
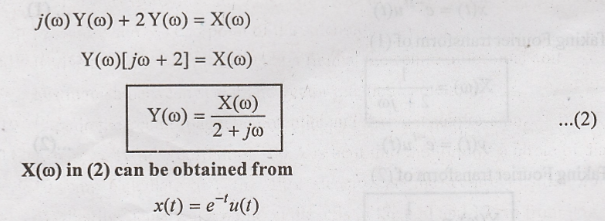
Taking Fourier
Transform
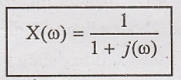
Now substitute X(ω) in
Y(ω)

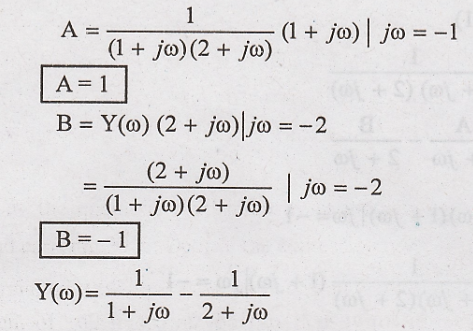
Taking inverse Fourier
transform
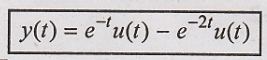
Problem 4:
Consider the continuous
time LTI system described by 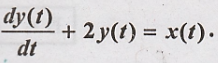 Using fourier
transform, find the output y(t) to each of the following input signals.
Using fourier
transform, find the output y(t) to each of the following input signals.
(i) x(t) = e-t
u(t) (ii) x(t) = u(t)
Solution:
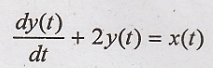
Taking Fourier
Transform

(i) x(t) = e-t
u(t)
Taking Fourier
Transform.
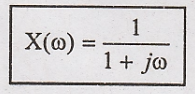
Now substitute X(ω) in
(1)

Taking inverse fourier
transform
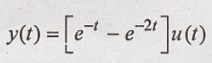
(ii) x(t) = u(t)
Taking Fourier
Transform
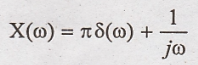
Now substitute X(ω) in
(1)
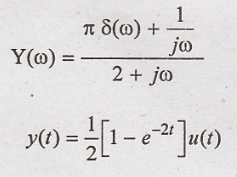
Problem 5:
A stable LTI system is
described by the differential equation.
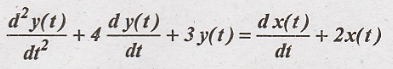
Find the frequency
response and impulse response using Fourier transform. [Dec 13-8Marks]
Solution:
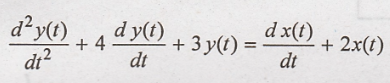
Taking Fourier
transform
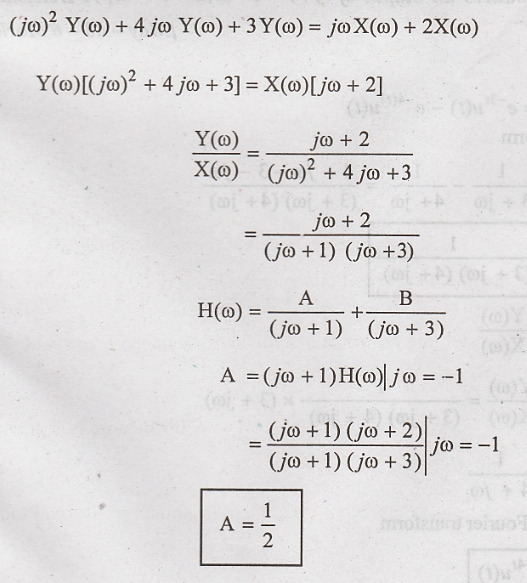
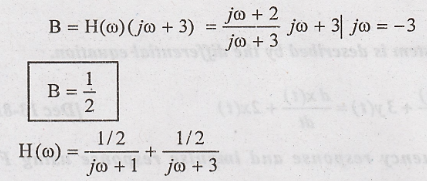
Taking inverse Fourier
transform.
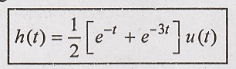
Problem 6:
Frequency response of
the causal LTI system is give by H(jω) = 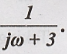 . The system produces an
output of
. The system produces an
output of 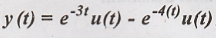 . Determine the input. [May-08-6 Marks]
. Determine the input. [May-08-6 Marks]
Solution:

Taking Fourier
transform

Taking inverse Fourier
transform
Problem 7:
The impulse response of
the continuous time system is given as 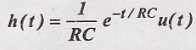 . Determine the frequency
response and plot magnitude and phase plot.
. Determine the frequency
response and plot magnitude and phase plot.
Solution:
Taking Fourier
transform of impulse response.

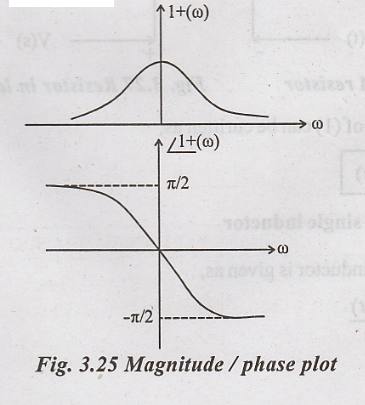
Magnitude of frequency
response
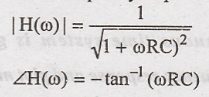
Signals and Systems: Unit III: Linear Time Invariant Continuous Time Systems,, : Tag: : CT Systems, Frequency Response, Solution of Differential Equations, Problems Based on Fourier Transform Analysis of CT Systems - Fourier Transform Analysis of CT Systems
Related Topics
Related Subjects
Signals and Systems
EC3354 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
