Random Process and Linear Algebra: Unit I: Probability and Random Variables,,
Exponential Distribution
Distribution Function of Exponential distribution, Memoryless Property of Exponential Distribution
Explain about the exponential distribution, distribution function of exponential distribution and memoryless property of exponential distribution
EXPONENTIAL DISTRIBUTION
i. Exponential distribution
A continuous random variable X is said
to follow exponential distribution if its probability density function is given
by,
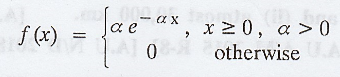
ii. Distribution function of Exponential Distribution
By definition, (D.F) 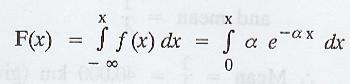
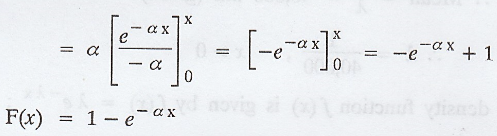
iii. Memoryless property of exponential distribution
[A.U Tvli M/J 2010] [A.U M/J 2013] [A.U
N/D 2016 R13 PQt] [A.U N/D 2019 R17 P&S]
If X is exponentially distributed, then
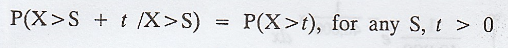
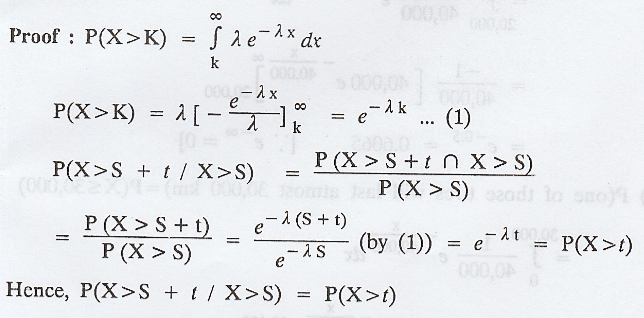
The converse of this result is also
true.
(i.e.,) If P(X > S + t / X > S) = P(X > t) then X follows an exponential distribution.
Example 1.11.1
The mileage which car owners get with a
certain kind of radial tyre is a random variable having an exponential
distribution with mean 40,000 km. Find the probabilities that one of these
tires will last (i) atleast 20,000 km and (ii) atmost 30,000 km. [A.U M/J 2009]
[A.U A/M 2015 R-8] [A.U N/D 2018 (R13) RP]
Solution:
Let X denotes the mileage obtained with
the tire and mean = 1/λ
.'. Mean = 1/λ = 40,000 km (given)
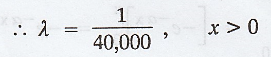
The density function f(x) is given by 
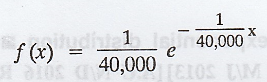
(i) P(one of the tires will last atleast
20,000 km) = P(X ≥ 20,000)
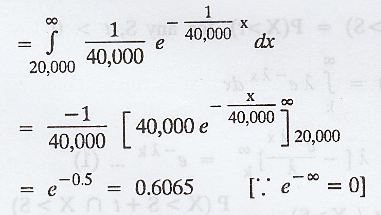
(ii) P(one of those tires will last
atmost 30,000 km) = P(X ≤ 30,000)
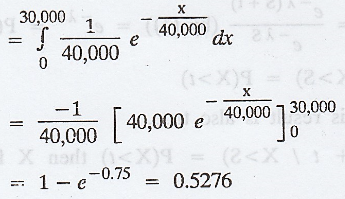
Example 1.11.2
The time in hours required to repair a
machine is exponentially distributed with perimeter λ = 1/2 (i) What is the
probability that the repair time exceeds 2h,
(ii) What is the conditional probability
that a repair takes atleast 10h given that its duration exceeds 9h ? [A.U M/J
2006] [A.U N/D 2010] [A.U M/J 2012] [A.U N/D 2017 (RP) R-08]
Solution:
Given λ = 1/2
Let 'X' denotes the time to repair the
machine.
The density function of X is given by,
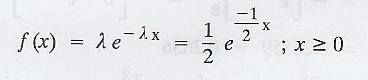
(i) P(the repair time exceeds 2h) = P(X
> 2) 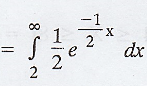

(ii) The conditional probability that a
repair takes atleast 10h given that its duration exceeds 9h is given by,
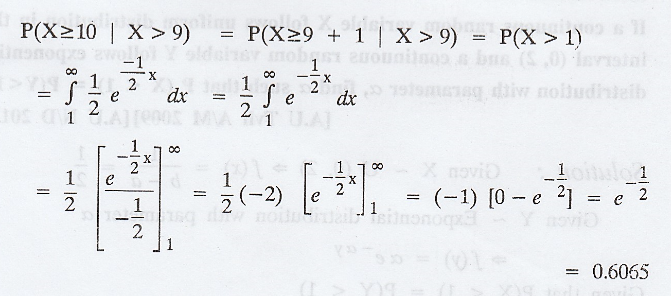
Example 1.11.3
The length of time a person speaks over
phone follows exponential distribution with mean 6. What is the probability
that the person will talk for (1) more than 8 minutes (2) between 4 and 8
minutes ? [A.U N/D 2006] [A.U M/J 2016 R13 RP]
Solution:
Given: f(x) = 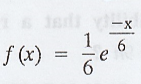

Example 1.11.4
If a continuous random variable X follows
uniform distribution in the interval (0, 2) and a continuous random variable Y
follows exponential distribution with parameter a, find a such that P (X <
1) = P(Y < 1). [A.U Tvli A/M 2009] [A.U N/D 2013]
Solution :
Given X ~ U (0, 2) => f(x) = 1/b-a = 1/2
Given Y - Exponential distribution with
parameter a
=> f (v) = a e-ay
Given that P(X < 1) = P(Y < 1)
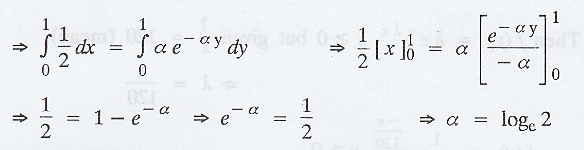
Example 1.11.5
If X is exponentially distributed with
parameter λ, find the value of K there exists P(X > K) / P(X ≤ K) = a.
Solution :
Given that 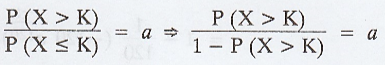
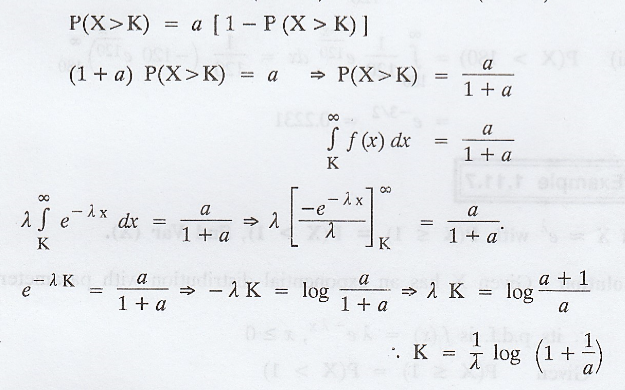
Example 1.11.6
The amount of time that a watch will run
without having to be reset is a R.V having an exponential distribution with
mean 120 days. Find the probability that such a watch will (i) have to be set
in less than 24 days and (ii) not have to be reset in atleast 180 days. [A.U
CBT A/M 2011] [A.U A/M 2018 R-08]
Solution:
Let 'X' denotes the number of days the
watch will run without reset.
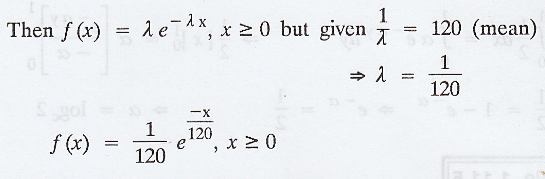
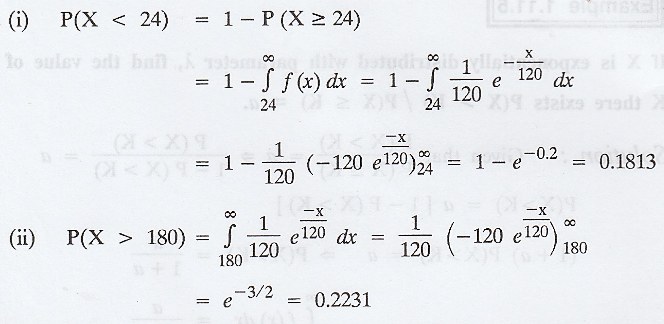
Example 1.11.7
If X ≈ eλ with P(X ≤ 1) = P(X
> 1), find Var (X).
Solution:
Given X has an exponential distribution
with parameter λ.
.'. its p.d.f. is f (x) = λ e-λx,
x ≥ 0
Given P(X ≤ 1) = P(X > 1)
1 - P (X > 1) = P (X > 1)
.'. 2 P( X > 1) = 1 => P(X > 1)
= 1/2
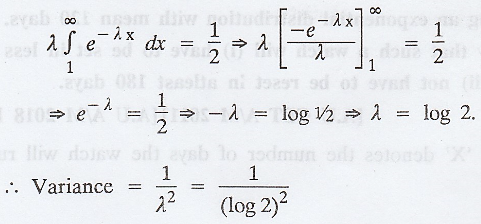
Example 1.11.8
If the number of kilometres that a car
can run before its battery wears out is exponentially distributed with an
average value of 10,000 km and if the owner desires to take a 5000 km trip,
what is the probability that he will be able to complete his trip without having
to replace the car battery. Assume that the car has been used for same time.
Solution :
Let X denotes the number of kilometres that a
car can run before its battery wears out.
Also given mean = 1/λ = 10,000 => λ =
1/10,000
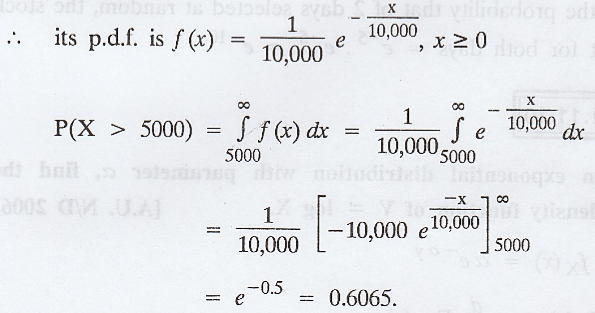
Example 1.11.9
The daily consumption of milk in excess
of 20,000 gallons is approximately exponentially distributed with = 3000. The
city has a daily stock of 35,000 gallons. What is the probability that of two
days selected at random, the stock is insufficient for both days.
Solution:
X -> Excess amount of milk consumed
in a day.
If 'Y' denotes the daily consumption of
milk, then X = Y - 20,000 follows the exponential distribution.
Given Mean θ = 1/λ = 3000
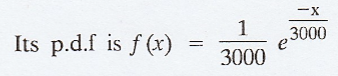
The probability that the stock is
insufficient for one day
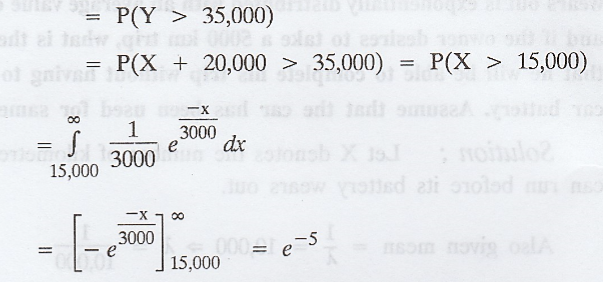
Hence, the probability that of 2 days
selected at random, the stock is insufficient for both days = e-5 . e-5 = e-10
Example 1.11.10
If X has an exponential distribution
with parameter a, find the probability density function of Y = log X. [A.U. N/D
2006]
Solution :
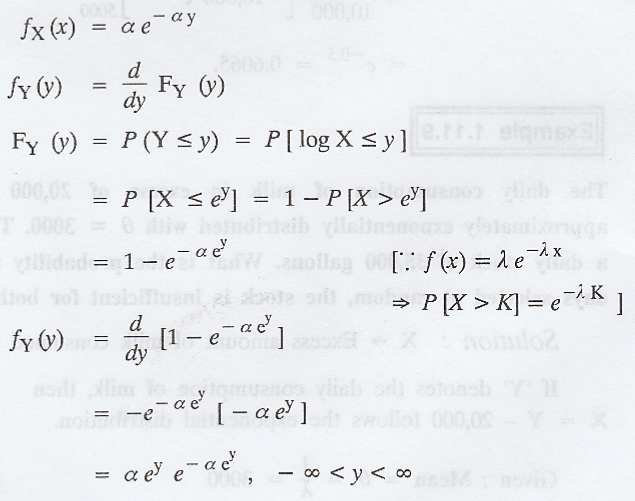
Example 1.11.11
If X is exponentially distributed, prove
that the probability that X exceed its expected value is less than 0.5
Solution:
Let X is exponentially distributed, its
p.d.f is

Thus, P (X > Expected value) < 0.5
Note that if M is the median (and not
the mean) of X then
P (X < M) = P(X > M) = 1/2
EXERCISE 1.11
1. The time in hours required to repair
a machine is exponentially distributed with parameter λ = 1/2, (i) what is the
probability that the repair time exceeds 2 hours? (ii) What is the conditional
probability that a repair takes atleast 10 hours given that its duration
exceeds 9 hours? [Ans. (i) 0.3679, (ii) 0.6065]
2. A continuous r.v. X has the p.d.f. f
(x) = 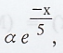 x > 0, find α, E[X] and var(X). [Ans. α = 1/5, E[X] = 5,
var[X] = 25]
x > 0, find α, E[X] and var(X). [Ans. α = 1/5, E[X] = 5,
var[X] = 25]
3. The mileage which a car owner gets
with a certain kind of tyre is a r.v. having an exponential distribution with
mean 40,000 kms. Find the probabilities that one of these tyres will last (i)
atleast 20,000 kms (ii) atmost 30,000 kms. [Ans. (i) 0.6065, (ii) 0.5270]
4. If the continuous r.v. X
exponentially distributed with parameter λ find the pdf of Y = X2. 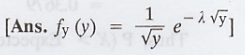
5. If the p.d.f of the r.v. X is f(x) =
e-x, x > 0 find the pdf of Y = X3. 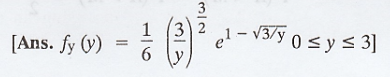
Random Process and Linear Algebra: Unit I: Probability and Random Variables,, : Tag: : Distribution Function of Exponential distribution, Memoryless Property of Exponential Distribution - Exponential Distribution
Related Topics
Related Subjects
Random Process and Linear Algebra
MA3355 - M3 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
