Examples of Vector Spaces

EXAMPLES OF VECTOR SPACES :

(a) Matrix space M_{m x n} :

The notation M_{m x n} or simply M, will be used to denote the set of all m x n matrices with entries from a field F. Then M_{m x n} is a vector space over F with respect to the usual operations of matrix addition and scalar multiplication of matrices.

Problem 1

Write the zero vector of M_{3 x 4} (F)

Solution :

Problem 2

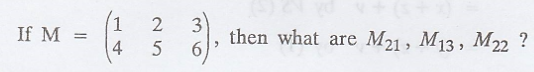
Solution :

Problem 3

Perform the indicated operationsord

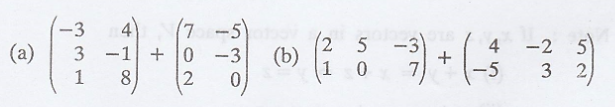
Solution :

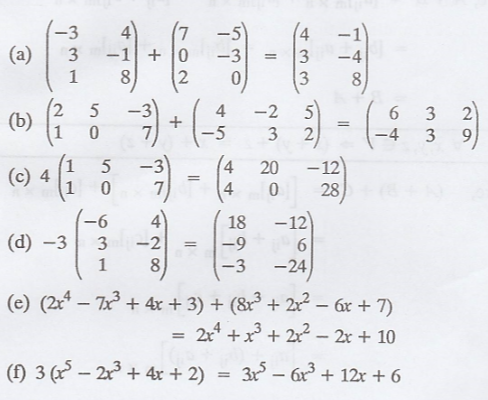
Problem 4

Let V denote the set of all m x n matrices with real entries. Let F be the field of rational numbers, defined by

Solution :

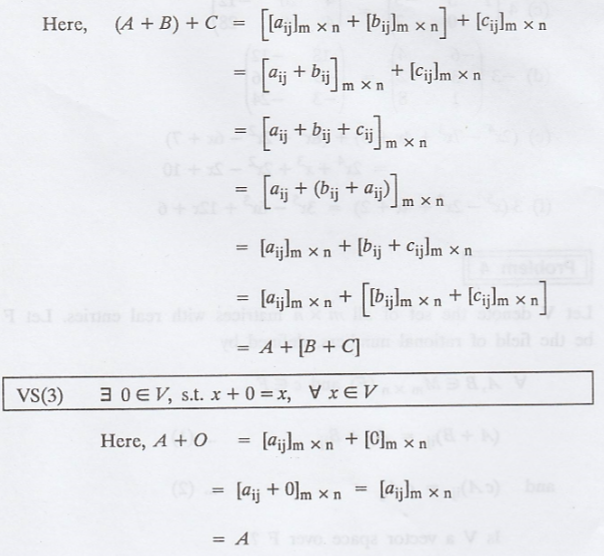
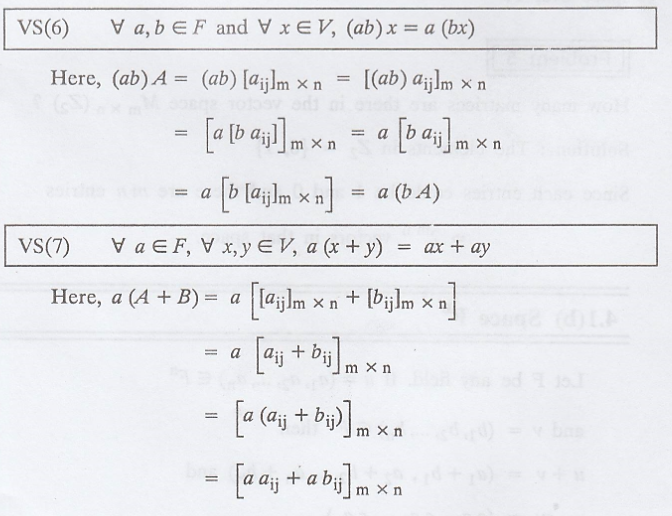
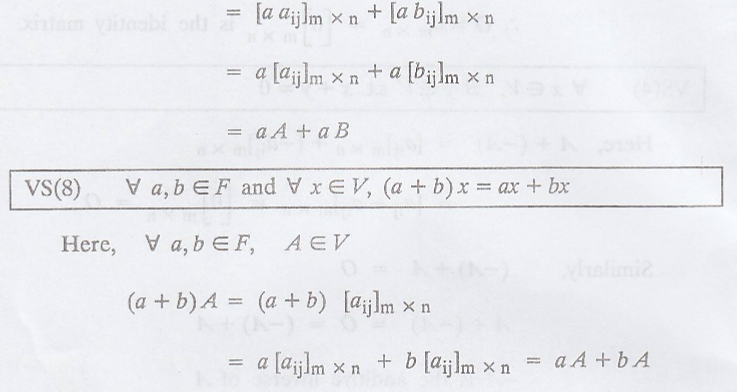
Hence, the proof.

i.e., The set of all m x n matrices with real entries is a vector space over F.

Problem 5

How many matrices are there in the vector space M_{m x n}(Z₂) ?

Solution:

The elements in Z₂{0, 1}

Since each ertries could be 1 and 0 and there are m n entries

→ 2^mn vectors in that space.

(b) Space Fⁿ

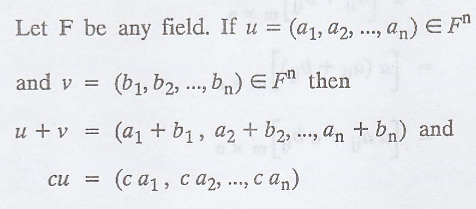
The zero vector in Fⁿ is the n-tuple of zeros 0 = (0, 0, ... 0) and the negative of a vector is defined by

Theorem :

In any vector space V, the following statements are true.

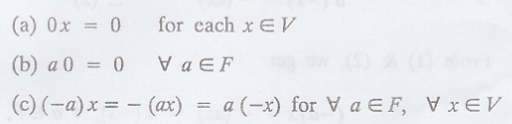
Proof :

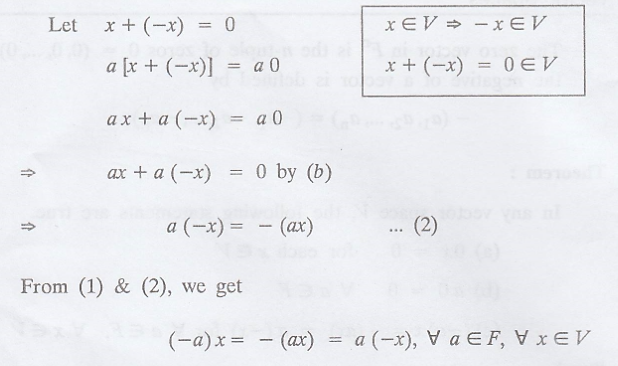
Corrollary 1.

Prove that in a vector space V, the additive identity is unique.

(or) Prove that in a vector space V, over a field F, the zero vector 0 of V is unique.

Proof :

Suppose 0 and 0' are two identity elements of V.

We have

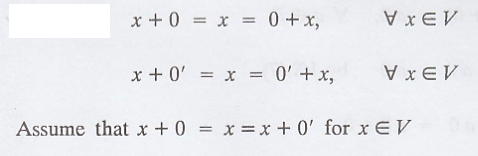
If 0' is an additive identity, then 0 + 0' = 0 ......(1)

If 0 is an additive identity, then 0 + 0' = 0 ......(2)

From (1) & (2), we get 0 = 0'

Hence, the identity element is unique.

Corrollary 2.

Prove that in a vector space V, the additive inverse is unique.

(or) Prove that in a vector space V over a field F the negative or the additive inverse -y in V of any vector y ε V is unique.

Proof :

Suppose y and y' are two additive inverse elements of V.

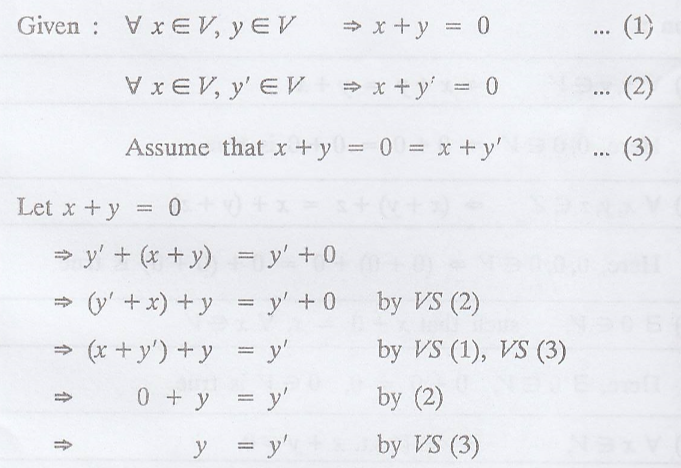
Note: The vector 0 in VS (3) is called the zero vector of V, and the vector y in VS (4) is called the additive inverse of x and is denoted by -x.

Problem 1.

In any vector space V, show that (a + b) (x + y) = ax + ay + bx + by for any x, y ε V and any a, b ε F

Solution :

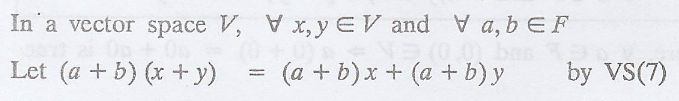
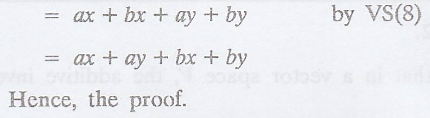
Problem 2.

Let V = {0} consist of a single vector 0 and define 0 + 0 = 0 and, a 0 = 0 for each scalar a in F. Prove that V is a vector space over F. (V is called the zero vector space)

Solution :

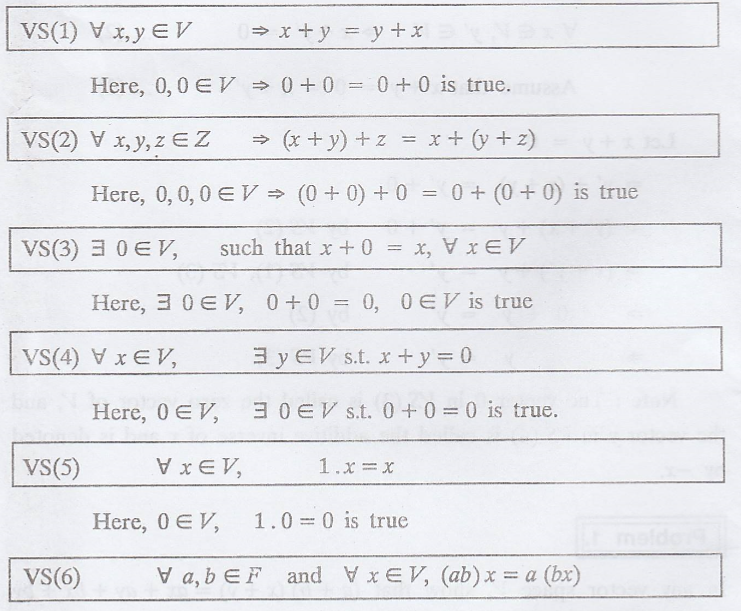
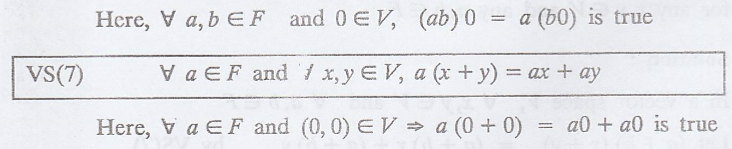
Problem 3.

Let V denote the set of ordered pairs of real numbers. If (a₁, a₂) and (b₁, b₂) are elements of V and c ε R, define

Is V a vector space over R with these operations? Justify your answer.

Solution :

No. If it is a vector space,

we have 0 (a₁, a₂) = (0, a₂) be the zero vector.

But a₂ is arbitrary.

This is a contradiction to the uniqueness of zero vector

Problem 4.

Let 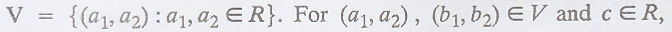 define

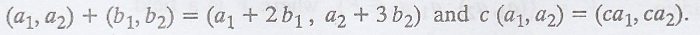
Is V a vector space over R with these operations? Justify your answer.

Solution :

Given:

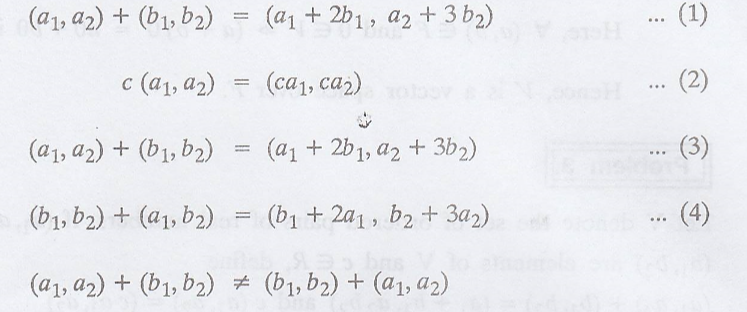
which is a contradiction to VS(1)

.'. V is not a vector space over R with these operations.

Problem 5.

Let 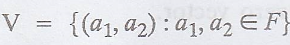, where F is a field. Define addition of elements of V co-ordinate wise, and for  define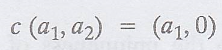 

Is V is a vector space over F with these operations? Justify your answer.

Solution :

Given:

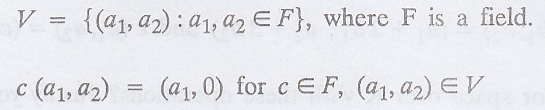
0 (a₁, a₂) = (a₁, 0) is the zero vector but which is a contradiction to VS(3) the zero vector to be unique.

.'. V is not a vector space over F with these operations.

Problem 6.

Let V be the set of all pairs (a, b) of real numbers.

Examine the following case V is a vector space over R or not.

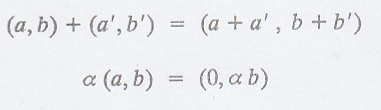
Solution:

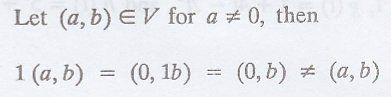
Thus VS(5) not satisfied.

Hence, V(R) is not a vector space.

Problem 7.

What is the zero vector in the vector space R⁴?

Solution :

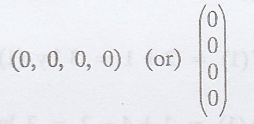
(c) Function space 

Example :

Let S be any non-empty set and F be any field.

Let  denote the set of all functions from S to F.

Two functions ƒ and g in 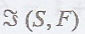 are called equal if ƒ (s) = g(s) for each s ε S.

The set  is a vector space with the operations of addition and scalar multiplication defined for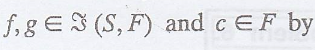 

Problem 1.

Solution :

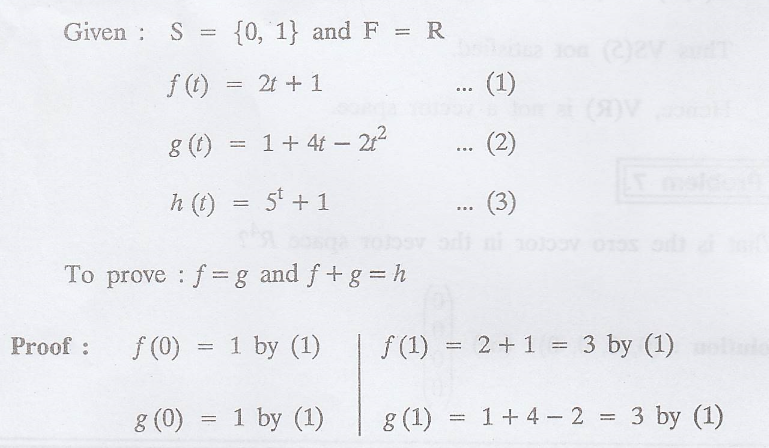
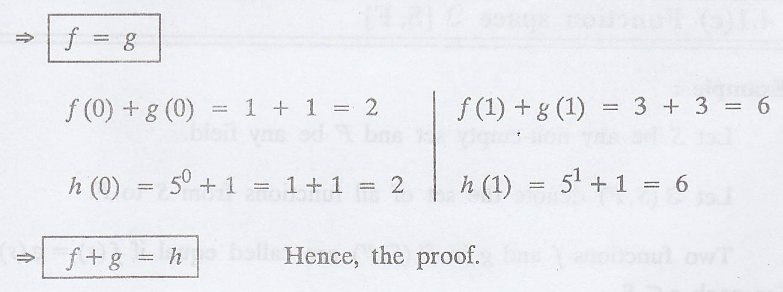
(d) Polynomial space P(F)

Example :

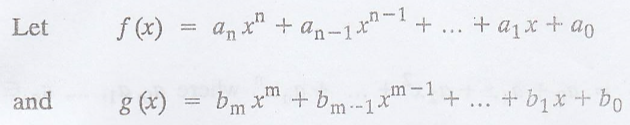
be polynomials with coefficients from a field F. Suppose that m ≤ n, and define 

Then g(x) can be written as

The set of all polynomials with coefficients from F is a vector space, which we denote by P (F).

Note :

1. If ƒ and g are polynomials of degree n, then f + g is not a polynomial of degree n.

2. If f is a polynomial of degree n and c is a non-zero scalar, then c f is a polynomial of degree n.

3. A non-zero scalar of F may be considered to be a polynomial in P(F) having degree zero.

Problem 1.

Prove that the set of all polynomials over a field F is a vector space V.

Solution :

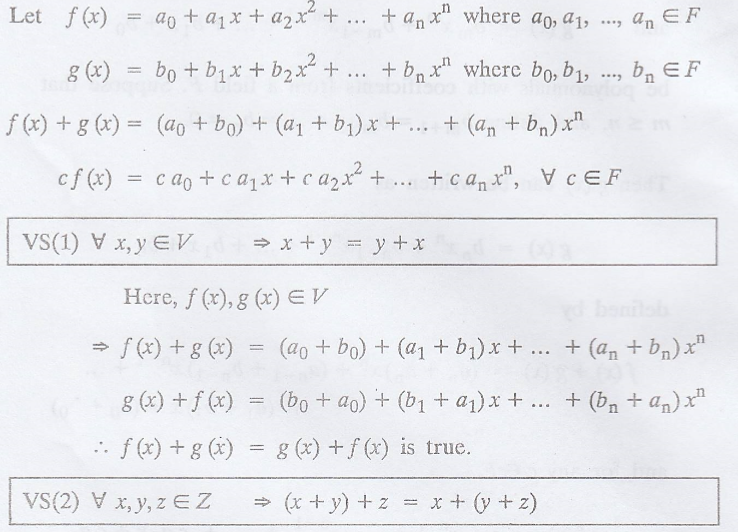
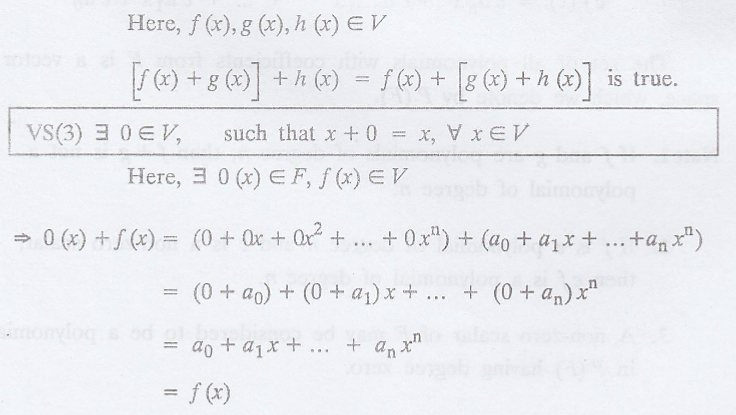
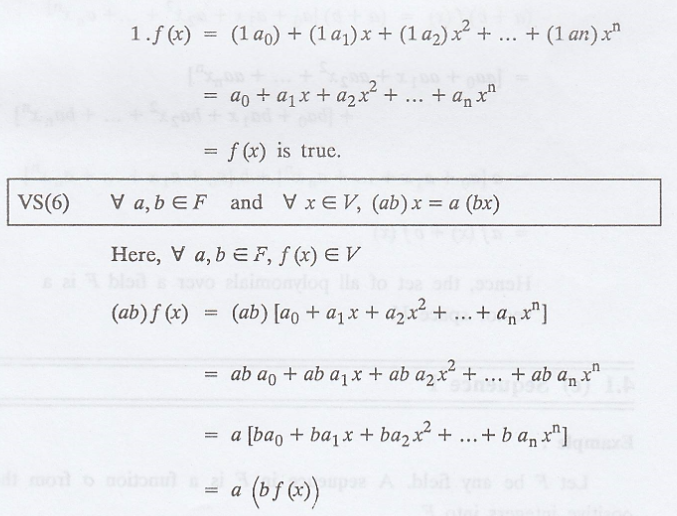
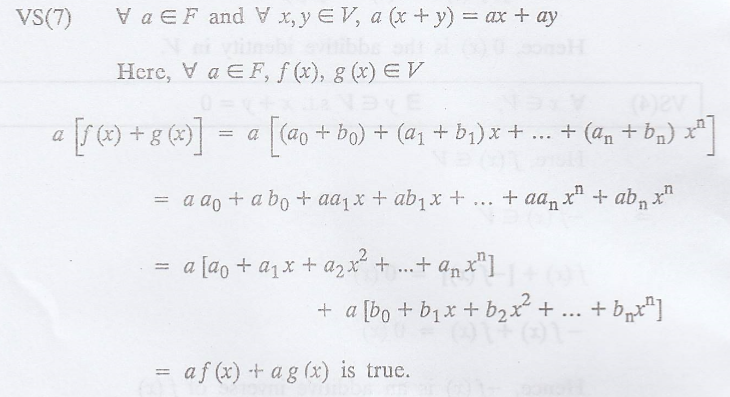
Hence, the set of all polynomials over a field F is a vector space V.

(e) Sequence F

Example :

Let F be any field. A sequence in F is a function o from the positive integers into F.

Let the sequence σ such that σ(n) = a_n, for n = 1, 2, ... is denoted {a_n}.

Let V consist of all sequences {a_n} in F that have only a finite number of non-zero terms a_n

With these operations V is a vector space.

Problem 1.

Let V be the set of sequences {a_n} of real numbers. For  and any real number t, define

Prove that, with these operations, V is a vector space over R.

Proof :

Given:

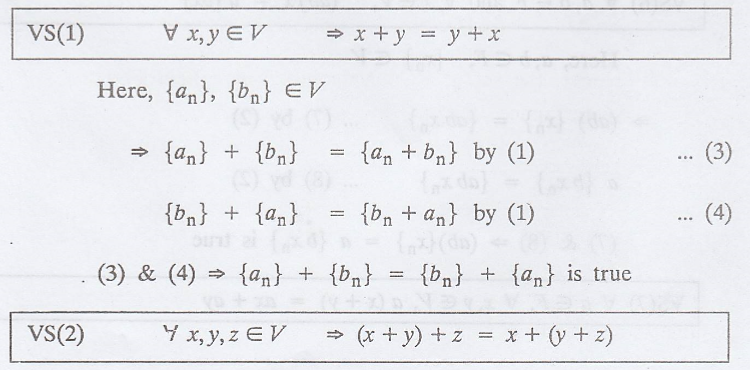
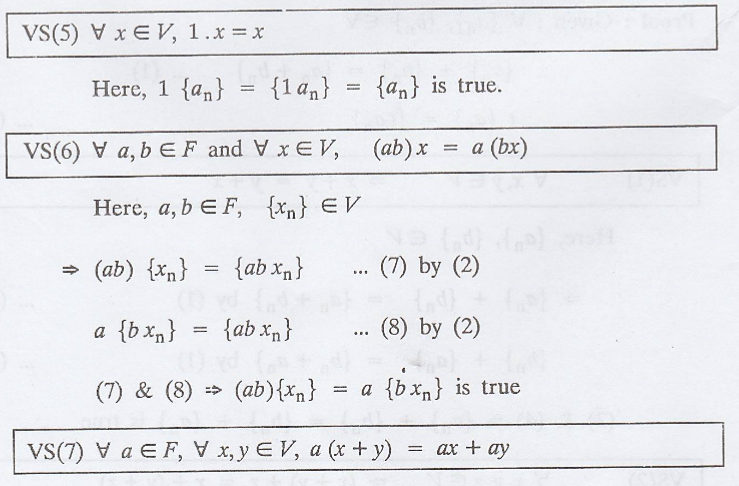
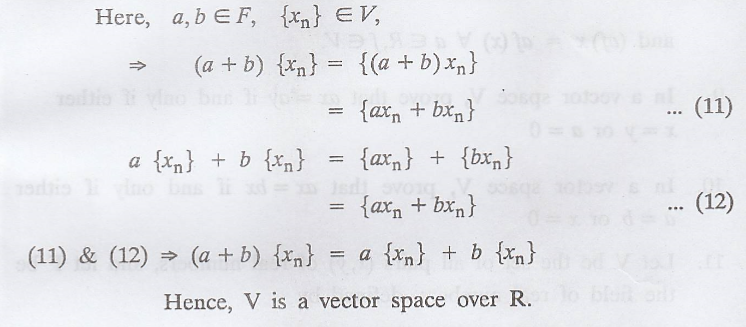
EXERCISE 4.1

1. Show that the space P of all polynomials is a vector space.

2. Verify in detail that R³ is a vector space.

3. Let V be the set of all real numbers, define u + v = 2u - v and cu = cu. Is V a vector space?

4. Let V be the set consisting of a single element 0. Let 0 + 0 = 0 and c 0 = 0. Show that V is a vector space.

5. If V is a vector space that has a non-zero vector, how many vectors are in V?

6. Describe all vector spaces having a finite number of vectors.

7. Show that the set M of n x n diagonal matrices over the field of reals is a vector space under the usual addition of matrices and the scalar multiplication of a matrix by a real number.

8. If V is the set of all real-valued continuous (differential or integrable) functions defined in some interval [0, 1]. Then show that V(R) is a vector space with addition and scalar multiplication defined as follows

9. In a vector space V, prove that ax = ay if and only if either x = y or a = 0

10. In a vector space V, prove that ax = bx if and only if either a = b or x = 0

11. Let V be the set of all pairs (x, y) of real numbers, and let F be the field of real numbers, defined by

Is V, with these operations, a vector space over the field of real numbers?

12. Let R be the field of real numbers and let P_n be the set of all polynomials (of degree atmost n) over the field R, prove that P_n is a vector space over the field R.

13. Prove that the set of all ordered n-tuples forms a vector space over a field F.

14. Prove that the set of all convergent sequences is a vector space over the field of real numbers