Ergodic Processes

ERGODIC PROCESSES

Ergodic processes are processes for which time and ensemble (statistical) averages are interchangeable. The concept of ergodicity deals with the equality of time and statistical averages.

Definition: Time Average :

If X (t) is a random process, then 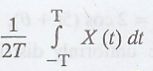 is called the time-average of X(t) over (-T, T) and is denoted by 

Note:

Definition: Ensemble Average:

The ensemble average of a random process {X(t)} is the expected value of the random variable X at time t.

i.e., Ensemble average = E[X(t)]

Definition: Ergodic process :

A random process X (t) is said to be ergodic, if its ensemble averages are equal to appropriate time averages.

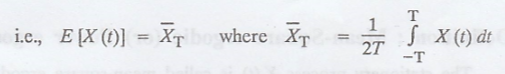
Note: In general, ensemble averages and time averages are not equal except for a special class of random processes called ergodic process.

Definition: Mean-Ergodic process:

A random process X(t) is said to be mean-ergodic, if

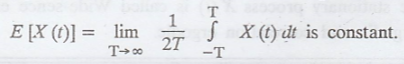
Note : To prove X (t) is mean-ergodic.

i.e., To prove E [X(t)] = 

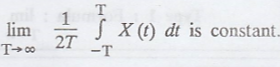
(or) To prove 

Definition: Correlation Ergodic process

The stationary process X (t) is correlation ergodic, if

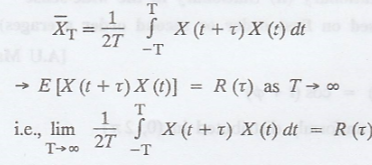
Definition: Distribution ergodic process

The stationary process X (t) is distribution ergodic, if

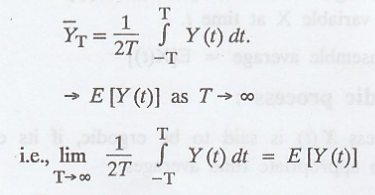
Definition: Mean-Square ergodic (or) Power ergodic.

The stationary process X (t) is called mean-square ergodic if

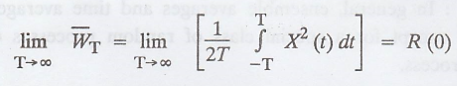
Definition: Wide-Sense ergodic (or) Weakly ergodic process

The stationary process X (t) is called Wide-sence ergodic if it is mean ergodic and correlation ergodic.

I. Example for Mean-Ergodic problem :

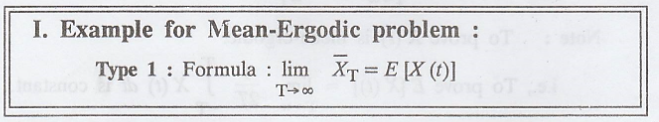
Example 1

Show that the random process X(t) = cos (t + φ), where φ is a random variable uniformly distributed in (0, 2л) is (i) First order stationary (ii) Stationary in the wide-sense (iii) Ergodic (based on first order or second order averages) [A.U May 2006]

Solution :

Given: X(t) = cos (t + φ)

where φ is uniformly distributed in (0, 2л)

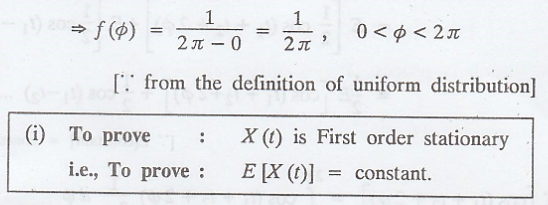
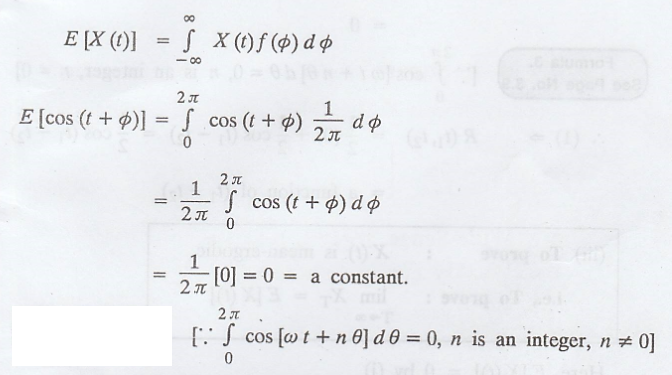
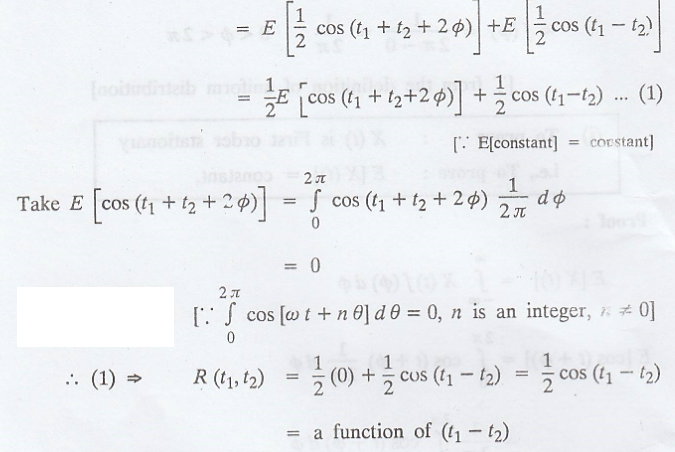
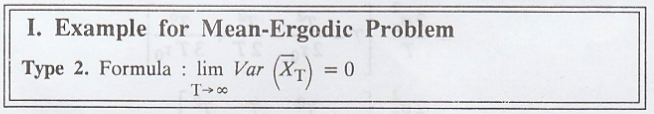
Example 2

If X(t) is a WSS process with mean µ and autocovariance function.

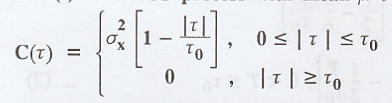
Find the variance of the time average of X(t) over (0, T). Also examine if the process X(t) is mean-ergodic.

Solution :

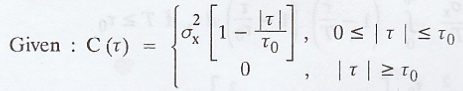
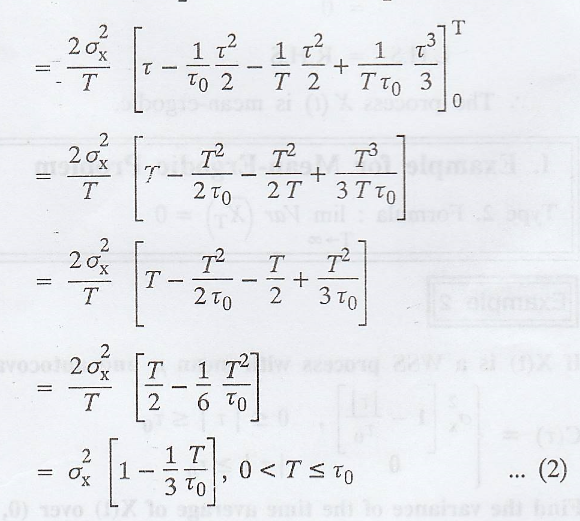
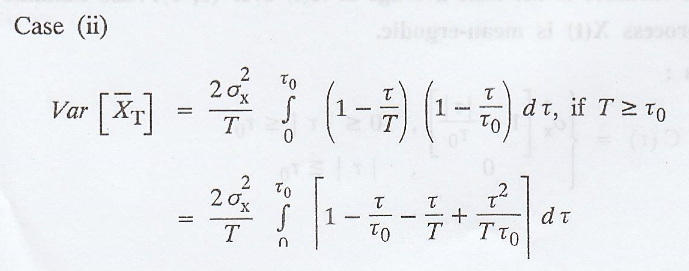
II. Example for not mean-ergodic

Example 3

If X(t) = A, where A is a random variable, prove that {X(t)} is not mean ergodic.

Solution:

Given: X (t) = A

Mean = E[X(t)] = E[A] = Ā .............(1)

We have to show that ensemble mean

≠ the mean in the time sense.

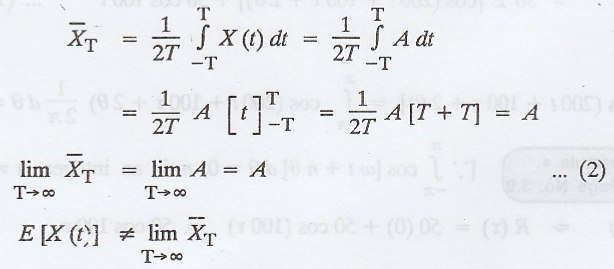
III. Example for Correlation-ergodic

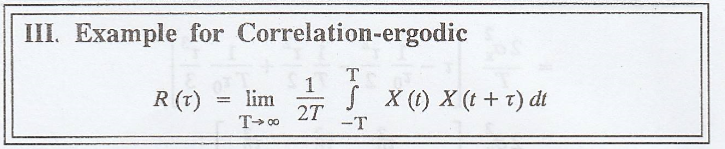
Example 4

Given that WSS random process X(t) = 10 cos (100 t + θ), where is θ uniformly distributed over (-л, л). Prove that the process X(t) is correlation-ergodic. [AU N/D 2003, N/D 2010, CBT N/D 2011]

Solution :

Given: X(t) = 10 cos (100 t + θ)

Given: X (t) is WSS process.

Take,

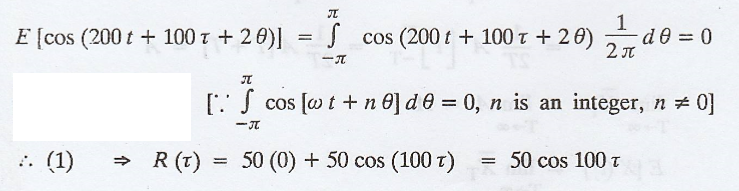
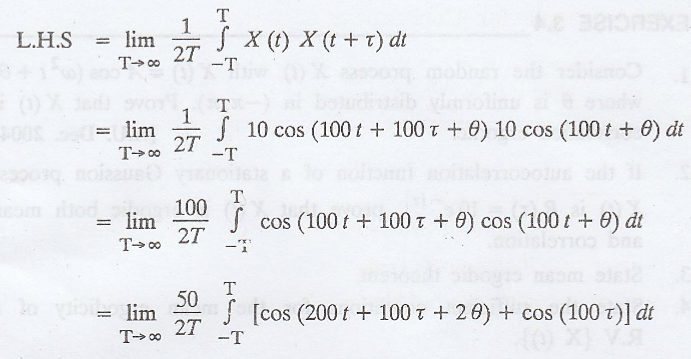
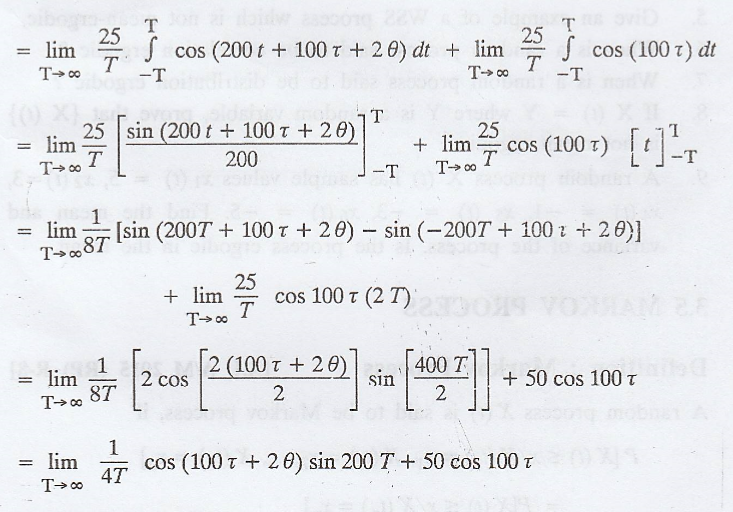
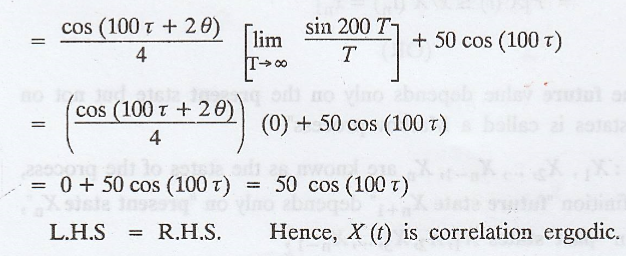
EXERCISE 3.4

1. Consider the random process X(t) with X(t) = A cos(ω²t + θ) where θ is uniformly distributed in (-л, л). Prove that X(t) is correlation ergodic. [A.U. Dec. 2004]

2. If the autocorrelation function of a stationary Gaussion process X(t) is R(t) = 10 e ^{- | τ |}, prove that X(t) is ergodic both mean and correlation.

3. State mean ergodic theorem.

4. State the sufficient conditions for the mean ergodicity of a R.V {X(t)}.

5. Give an example of a WSS process which is not mean-ergodic.

6. When is a random process said to be correlation ergodic ?

7. When is a random process said to be distribution ergodic ?

8. If X(t) = Y where Y is a random variable, prove that {X(t)} is not mean ergodic.

9. A random process X(t) has sample values x₁(t) = 5, x₂(t) = 3, x₄(t) = -1, x₅(t) = -3, x₆(t) = -5. Find the mean and variance of the process. Is the process ergodic in the mean.