Discrete Time Fourier Transform (DTFT)

DISCRETE TIME FOURIER TRANSFORM (DTFT)

The Fourier transform of discrete-time signal is called the discrete-time fourier transform (DTFT).

If x(n) is the given discrete time sequence, then X(ω) or X(e^jω) is the discrete- time Fourier transform of x(n).

The DTFT of x(n) is defined as:

The inverse DTFT of X(ω) is defined as:

We also refer to x(n) and X(ω) as a Fourier transform pair and this relation is expressed as.

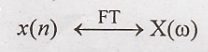
Existence of DTFT

The Fourier transform exists for a discrete-time sequence x(n) if and only if the sequence is absolutely summable, i.e. the sequence has to satisfy the condition.

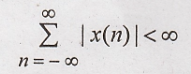
The DTFT doesnot exist for the sequences that are growing expononentially (ex. aⁿ . u(n), a >1) since they are not absolutely summable.

Relation Between Z - Transform and Fourier Transform

The z-transform of a discrete sequence x(n) is defined as:

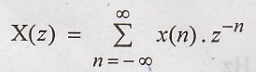
Where z - is a complex variable.

The Fourier transform of a discrete time sequence x(n) is defined as:

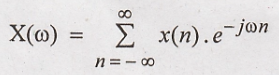
The X(z) can be viewed as a unique representation of the sequence x(n) in the complex z - plane.

The RHS is the Fourier transform of x(n). r^-n, i.e. the z-transform of x(n) is the Fourier transform of x(n).r^-n.

When r = 1

The RHS is the Fourier transform of x(n). So we can conclude that the Fourier transform of x(n) is same as the Z-transform of x(n) evaluated along the unit circle centered at the origin of the z-plane.

Properties of Discrete Time Fourier Transform

Linearity Property

The Linearity property of DTFT states that if

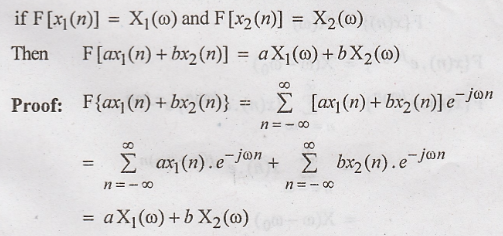
Periodicity Property

The periodicity property states that the DTFT X(ω) is periodic in ω with period 2π.

X(ω + 2nπ) = X(ω)

Time Shifting Property

The time shifting property of DTFT states that

If F[x(n)] = X(ω)

Then F[x(n-m)] = e ^{–j ω m} X(ω) where m is an integer.

Proof:

This result shows that the time shifting of a signal by m- units doesnot change its amplitude spectrum but the phase spectrum is changed by -ωm.

Frequency Shifting property

The Frequency shifting property of DTFT states that,

Proof :

This property is the dual of the time shifting property.

Time Reversal Property

The time reversal property of DTFT states that

That is folding in the time domain corresponds to the folding in the frequency domain.

Differentiation In Frequency Domain Property

The differentiation in the frequency domain property of DTFT states that,

Proof:

Differentiating both sides with respect to 'ω' we get

Time Convolution Property

The time convolution property of DTFT states that.

Proof:

Interchanging the order of summations we get

Put n - k = p in the second summation.

n = p + k

That is the convolution of the signals in the time domain is equal to multiplying their spectra in the frequency domain.

Frequency Convolution Property

The frequency convolution property of DTFT states that

Proof :

Interchanging the order of summation and integration we get.

This operation is known as periodic convolution because it is the convolution of two periodic function X₁(ω) and X₂(ω).

The Correlation Theorem

The correlation theorem of DTFT states that

The function is called the cross energy spectrum of the signals x₁(n) x₂(n).

The Modulation Theorem

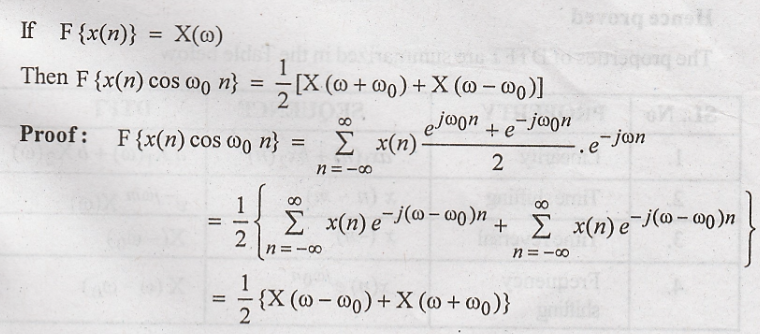
Parseval's Theorem

Interchanging the order of summation and integration we get

Hence proved

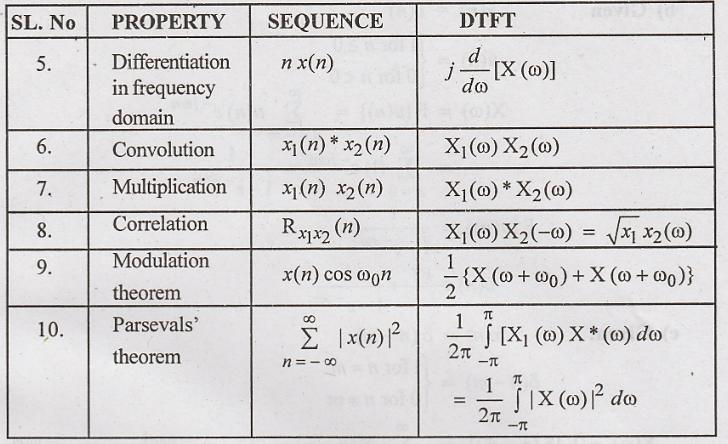
The properties of DTFT are summarized in the Table below

Example Problems Based on DTFT

Problem 1:

Find the DTFT of the following sequence:

(a) δ(n)

(b) u(n)

(c) δ(n-m)

(d) u(n-m)

(e) an u(n)

(f) -an u(-n-1)

(g) δ(n + 3) − δ(n − 3)

(h) u(n + 3) – u(n − 3)

Solution:

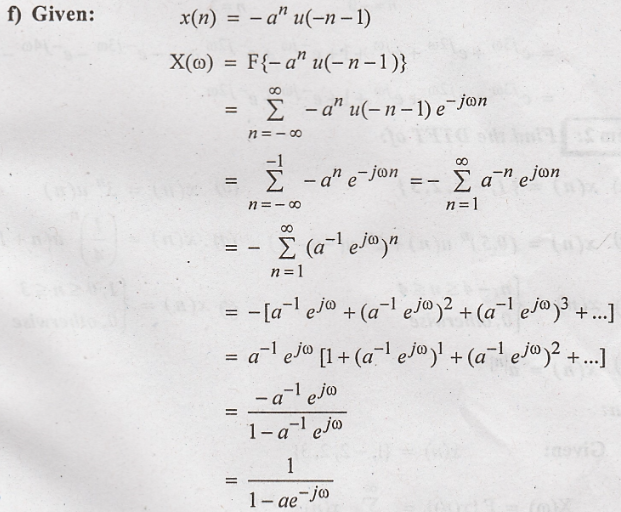
Problem 2:

Find the DTFT of:

Solution:

(b) Given x(n) = 3ⁿ u(n). The given sequence is not absolutely summable. Therefore, its DTFT does not exists.

(c) Given x(n) = (0.5)ⁿ u(n) + 2ⁿ u(−n−1)

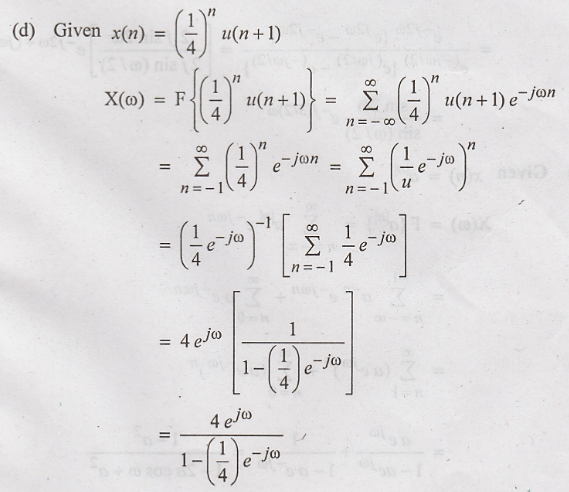
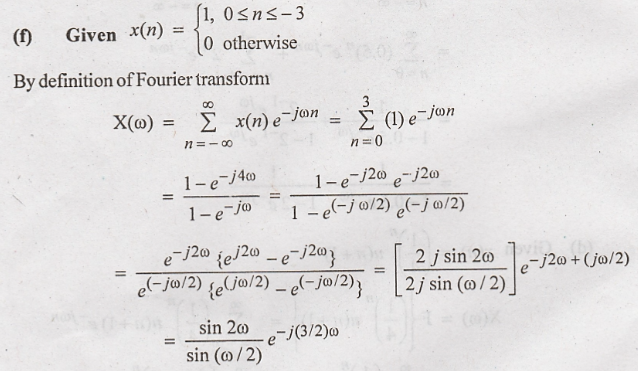
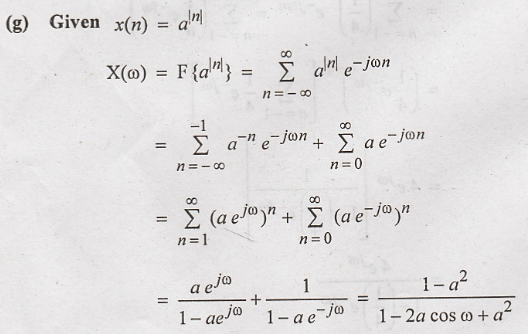
Problem 3:

Find the DTFT of the following sequences:

Solution:

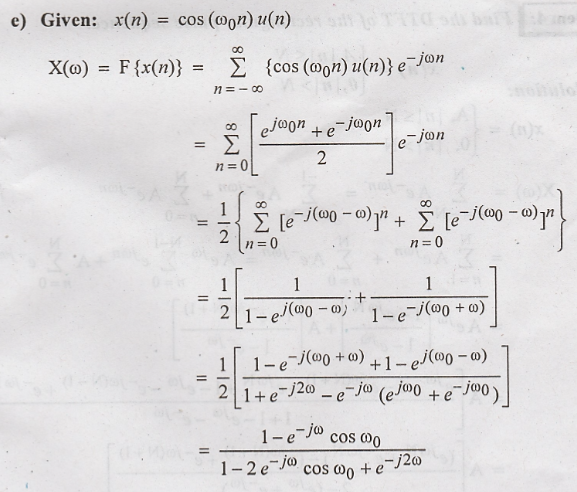
Problem 4:

Find the DTFT of the rectangular pulse sequence:

Solution: