Discrete Parameter Markov Process [Markov Chain]

Discrete Parameter Markov Process [Markov Chain]

- Chapman Kolmogorov equations - Limiting distributions

A discrete parameter Markov process is called a Markov Chain.

Note: Mathematically, we define the Markov Chain as follows

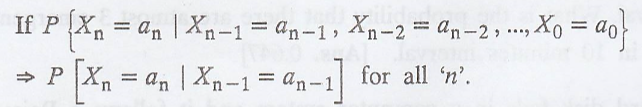
then the process X_n; n = 0, 1, 2, ... are called as Markov Chain. Here a₁, a₂, ..., a_n are called the states of the Markov chain.

Example :

The simple random walk moves, at each step, to a randomly chosen nearest neighbour.

Definition: One-step Transition Probability

The conditional probability P {X_n = a_j | X_n-1 = a_i} is called the one-step transition probability from state a_i to state a_j at the nth step (trial) and is denoted by P_ij (n-1, n).

Definition : Homogeneous Markov Chain

If P_ij (n-1, n) = P_ij (m-1, m), then the Markov Chain is called the homogeneous Markov Chain or the Chain is said to have stationary transition probabilities.

Note: The use of the word 'Stationary' does not imply a stationary random sequence.

Definition : Transition Probability Matrix (TPM)

When the Markov Chain is homogeneous, the one step transition probability is denoted by P_ij. The matrix P = {P_ij} is called (one-step) transition probability matrix (tpm).

Note: The tpm of a chain is a Stochastic matrix, since all P_ij ≥ 0 and the sum of all elements of any row of the transition matrix is equal to 1.

Definition: n-Step Transition Probability [A.U A/M 2019 R13 PQT]

The conditional probability that the process is state a_j at step n, given that it was in state a_i at step 0. (i.e.,) P{X_n = a_j / X_n = a_i} is called the n-step transition probability and denoted by 

Note :

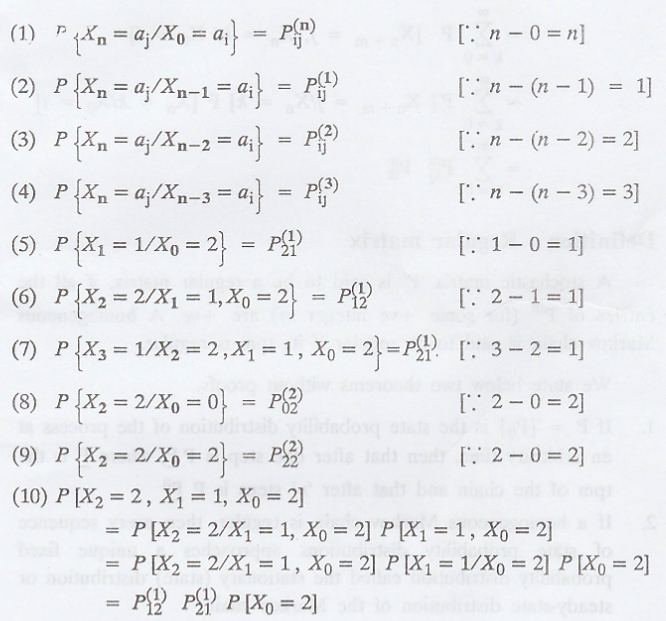
Definition: Chapman - Kolmogorov Theorem :

If 'P' is the tpm of a homogeneous Markov chain, then the n-step tpm p⁽ⁿ⁾ is equal to pⁿ.

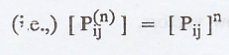
Derive the Chapman-Kolmogorov equations for discrete-time Markov chain.

[A.U. N/D 2007, A.U A/M 2015]

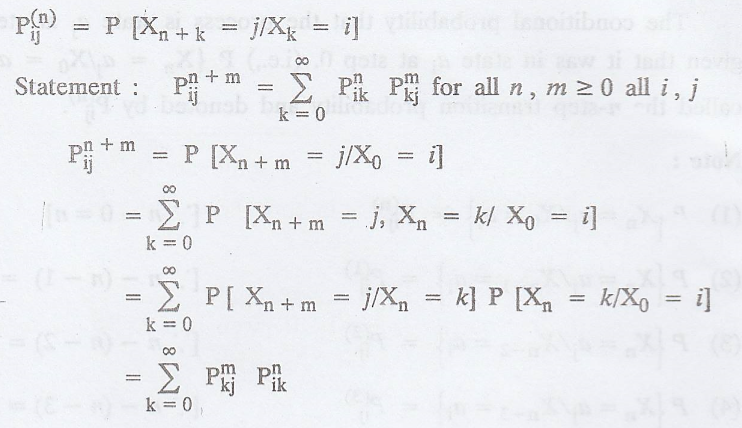
Definition: Regular matrix

A stochastic matrix 'P' is said to be a regular matrix, if all the entries of pm (for some +ve integer m) are +ve. A homogeneous Markov chain is said to be regular if its tpm is regular.

We state below two theorems without proofs.

1. If P = {Pij} is the state probability distribution of the process at an arbitrary time, then that after one step is P, where  is the tpm of the chain and that after 'n' steps is P

2. If a homogeneous Markov chain is regular, then every sequence of state probability distributions approaches a unique fixed probability distribution called the stationary (state) distribution or steady-state distribution of the Markov chain.

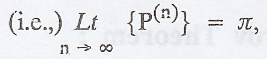 where the state probability distribution at step n,

3. Moreover, if 'P' is the tpm of the regular chain, then лP = π (π is a row vector). Using this property of л, it can be found out.

Hint :

Steady state (or) invariant (or) stationary (or) limiting-state (or) 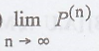 (or) long run (or) thousandth trial these are represents the same л

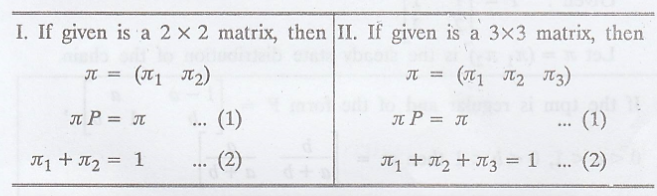
Note :-

(1) When all the entries of a tpm are positive,

i.e., if the tpm is regular and of the form

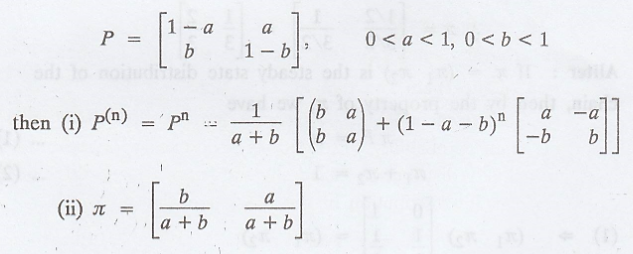
(2) If the tpm of a chain is a stochastic matrix, then the sum of all elements of any row is equal to 1.

Example 3.7.1

If the tpm of a Markov chain is 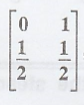 find the steady statedaistribution of the chain. [A.U N/D 2019 R17 PQT] [A.U A/M 2019 R17 PQT] 51832-gnitimil [AU CBT Dec. 2009, Trichy M/J 2011, Tvli M/J 2011] [A.U M/J 2013] [A.U A/M 2017 R-8] [A.U A/M 2018 R-13]

Solution:

Given: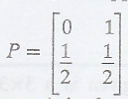 

Let л = (л1, л2) is the steady state distribution of the chain.

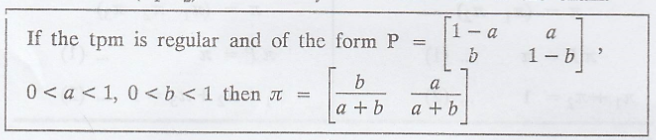
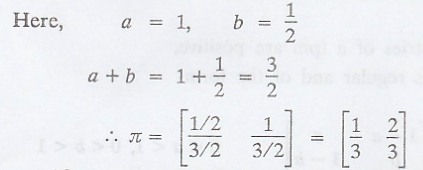
Aliter : If π = (π₁, π₂) is the steady state distribution of the chain, then by the property of л, we have

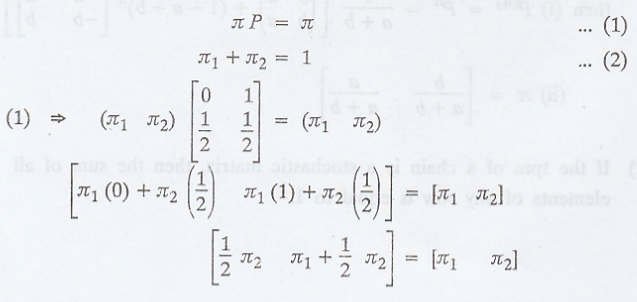
Example 3.7.2

The three-state Markov chain is given by the tpm 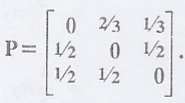 Find the steady-state distribution of the chain.

Solution:

If π = (π₁ π₂ π₃) is the steady-state distribution of the chain, then by the property of π, we have

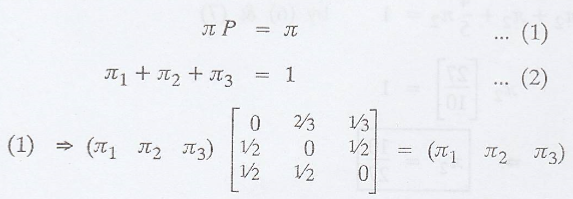
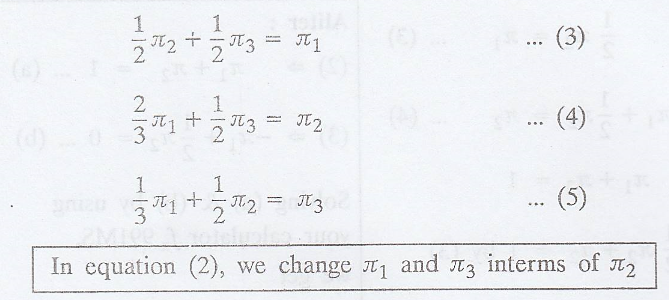
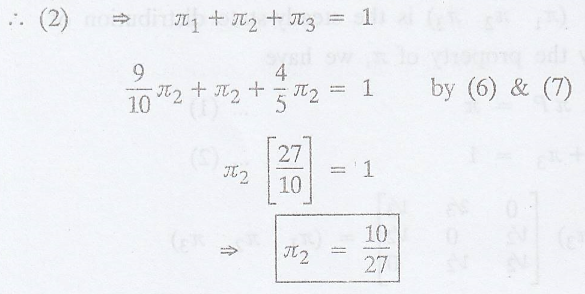
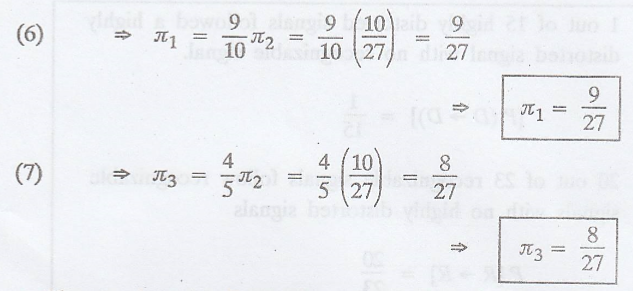
.'. The steady state distribution of the chain is

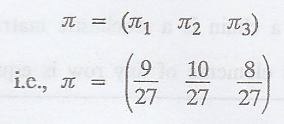
Example 3.7.3

An Engineer analyzing a series of digital signals generated by a testing system observes that only 1 out of 15 highly distorted signals followed a highly distorted signal with no recognizable signal, whereas 20 out of 23 recognizable signals follow recognizable signals with no highly distorted signals between. Given that only highly distorted signals are not recognizable. Find the fraction of signals that are highly distorted. [AU Dec. 2004, N/D 2007, M/J 2009, N/D 2010, N/D 2014] [A.U A/M 2015]

Solution :

Let π₁ -> the fraction of signals that are recognizable. [R]

π₂ -> the fraction of signals that are highly distorted. [D]

The tpm of the Markov chain is

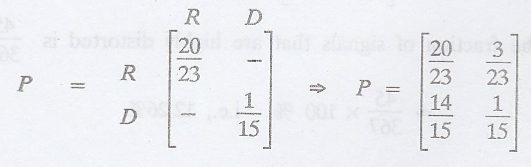
Example 3.7.4.

A student's study habits are as follows: If he studies one night, he is 70% sure not to study next night. On the otherhand, if he does not study one night, he is 60% sure not to study the next night as well. In the long run, how often does he study?

Solution :

Let π₁ -> he studies one night [S]

π₂ -> he does not study one night [N]

The tpm of the Markov Chain is

Let π = (π₁, π₂) is the steady state distribution of the chain.

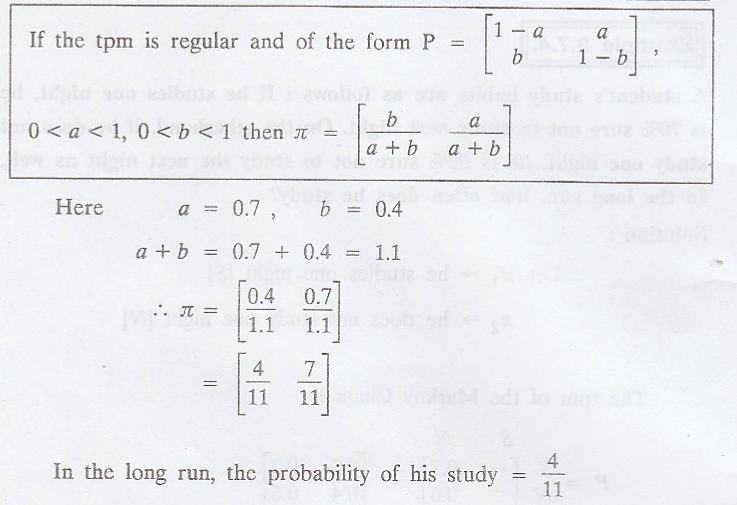
Example 3.7.5.

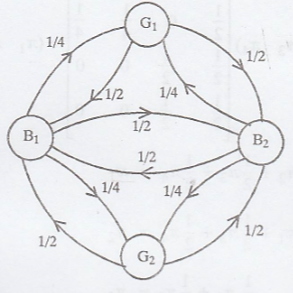
Two boys B₁, B₂ and two girls G₁, G₂ are throwing a ball from one to another. Each boy throws the ball to the other boy with probability 1/2 and to each girl with probability 1/4. On the other hand, each girl throws the ball to each boy with probability 1/2 and never to the other girl. In the long run, how often does each receive the ball? [A.U CBT N/D 2011] [A.U N/D 2013 R-08]

Solution :

Let π₁ -> boy (B₁)

π₂ -> boy (B₂)

π₃ -> girl (G₁)

π₄ -> girl (G₂)

The transition diagram is

.'. The tpm of the Markov Chain is

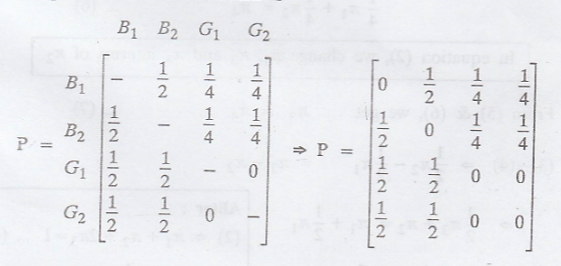
['.' If the tpm of a chain is a stochastic matrix, then the sum of all elements of any row is equal to 1]

If π = (π₁ π₂ π₃ π₄) is the steady state distribution of the chain, then by the property of л, we have

πP = 1 .............(1)

π₁ + π₂ + π₃ + π₄ = 1 .............(2)

.'. The steady state distribution of the chain is

π = (π₁ π₂ π₃ π₄)

i.e., π = (1/3 1/3 1/6 1/6)

Thus, in the long run, the probability that each boy receives the ball = 1/3, the probability that each girl receives the ball = 1/6

Example 3.7.6.

A salesman's territory consists of three cities A, B and C. He never sells in the same city on successive days. If he sells in A, then the next day he sells in city B. However, if he sells in either B or C, then the next day he is twice as likely to sell in city A as in the other city. In the long run, how often does he sell in each of the cities? [A.U M/J 2013] [A.U N/D 2013, M/J 2012] [A.U A/M 2017 R-8, N/D 2017 R-8]

Solution :

Let π₁ -> City A

π₂ -> City B

π₃ -> City C

.'. The tpm of the Markov chain is

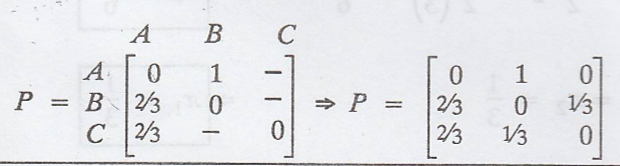
If π = (π₁ π₂ π₃) is the steady state distribution of the chain, then by the property of π, we have

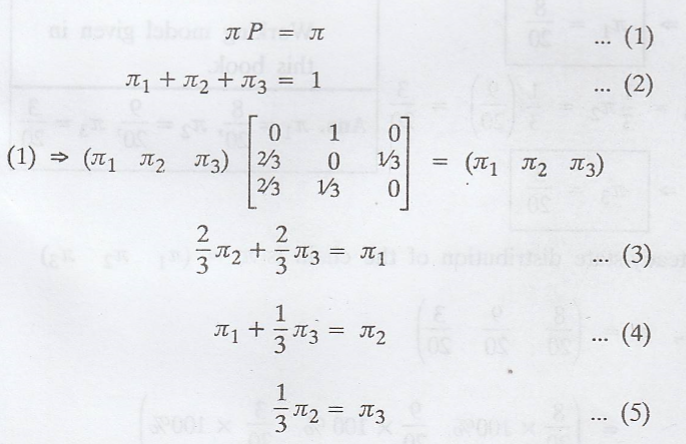
In equation (2), we change π₁ and π₃ interms of π₂

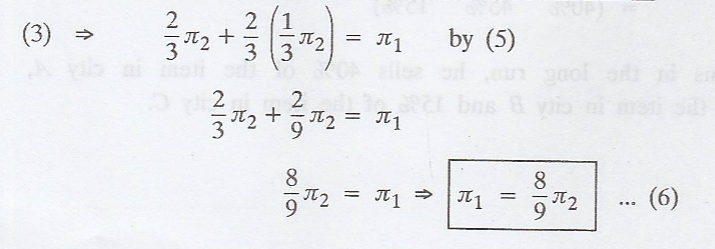
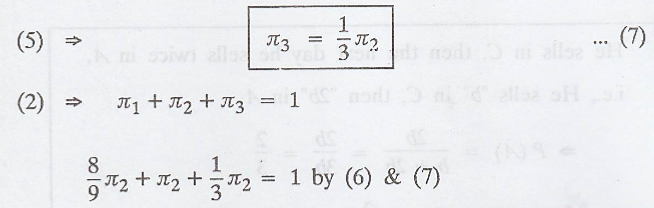
.'. The steady-state distribution of the chain is π= (π₁ π₂ π₃)

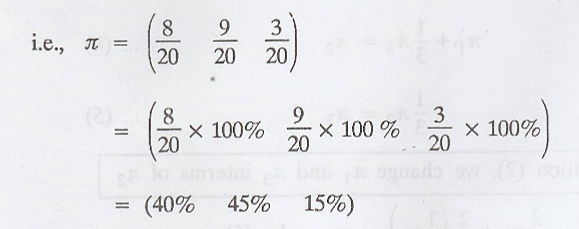
Thus in the long run, he sells 40% of the item in city A, 45% of the item in city B and 15% of the item in city C.

Example 3.7.7.

A housewife buys 3 kinds of cereals A, B and C. She never buys the same cereal in successive weeks. If she buys cereal A, the next week she buys cereal B. However if she buys B or C, the next week she is 3 times as likely to buy A as the other cereal. In the long run how often she buys each of the 3 cereals? [CBT A/M 2011, Trichy M/J 2011] [AU Tvli. M/J 2010]

Solution:

Given: Let π₁ → Cereal А; π₂ → Cereal В; π₃ → Cereal C

.'. The tpm of the Markov chain is

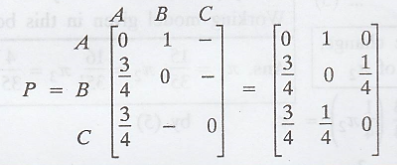
If π = (π₁ π₂ π₃) is the steady-state distribution of the chain, then by the property of π, we have

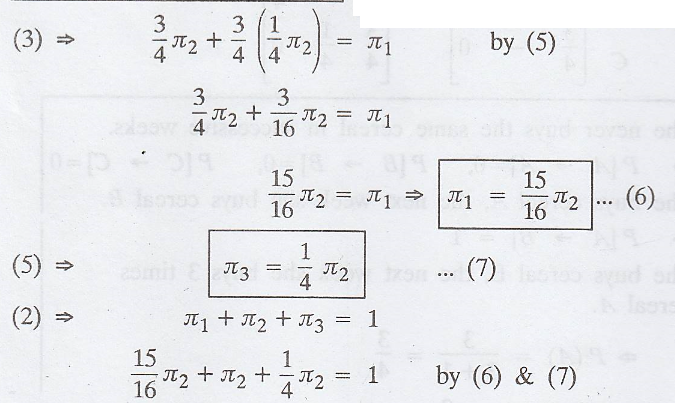
Example 3.7.8.

A man is at an integral part on the X-axis between the origin and the point 3. He takes a unit step to the right with probability or 1/3 to the left with probability 2/3, unless he is at the origin, where he of takes a step to the right to reach the point 1 or is at the point 3, where he takes a step to the left to reach the point 2. What is the probability that he is at the point 1 in the long run?

Solution:

The transition diagram is

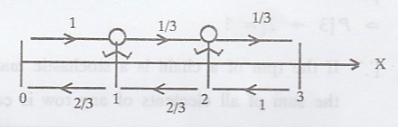
Given:

Let π₁ → Integral part 0, π₂ → Integral part 1,

π₃ → Integral part 2, π₄ → Integral part 3

.'. The tpm of the Markov chain

If π = (π₁ π₂ π₃ π₄) is the steady-state distribution of the chain, then by the property of π, we have

πP = π .............(1)

π₁ + π₂ + π₃ + π₄ = 1 .............(2)

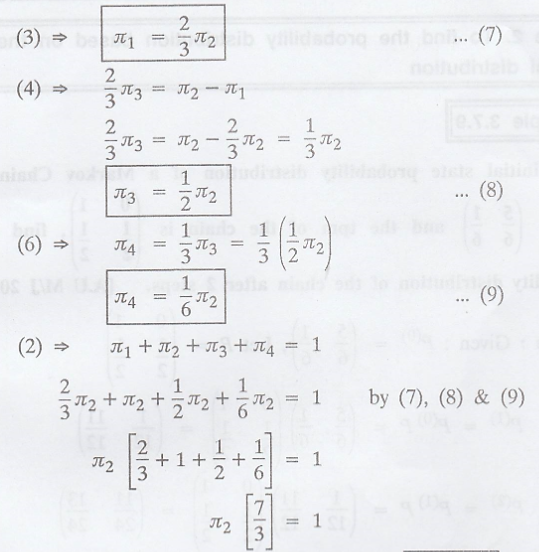
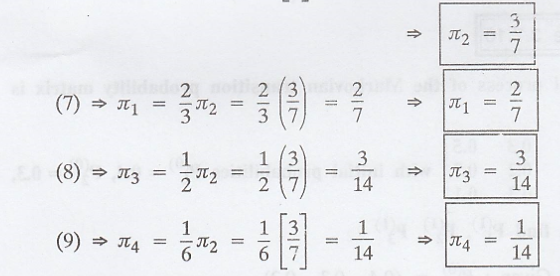
The steady-state distribution of the chain is

π = (π₁ π₂ π₃ π₄)

i.e., π = (2/7 3/7 3/14 1/14)

.'. The probability that he is at 1 after a long run = 3/7