Signals and Systems: Unit III: Linear Time Invariant Continuous Time Systems,,
Convolution
Concept of convolution, Properties of Convolution
Discuss about the topic of Convolution, Properties of convolution and problems about Convolution
3.5
CONVOLUTION
Concept of convolution
Convolution is a
mathematical operation which is used to express the input- output relationship
of an LTI system. It is a most important operation in LTI continuous -time
system. It relates input and impulse response of the system to output.
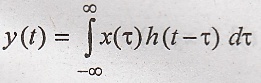
This is called
convolution integral, or simply convolution. The convolution of two signals
x(t) and h(t) can be represented as:
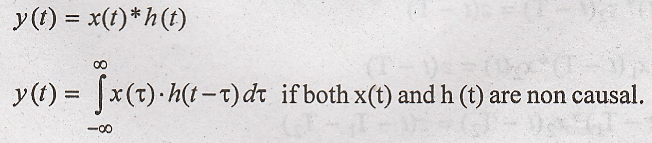
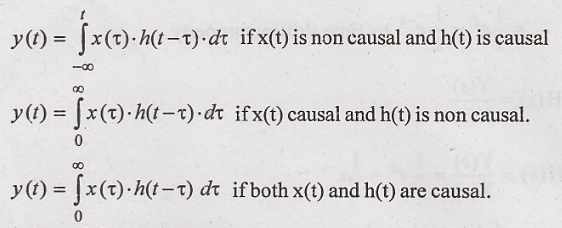
Properties of Convolution
Let us consider two
signals x1(t) and x2(t). The convolution of two signals x1(t)
and x2(t) is given by
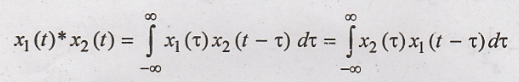
The properties of
convolution are as follows:
Commutative Property:
The commutative
property of convolution states that x1(t) * x2(t) = x2(t)
* x1(t).
Distributive Property:
The Distributive
property of convolution states that
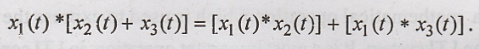
Associative Property:
The associative
property of convolution states that
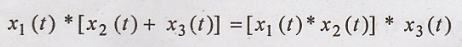
Shift Property:
The Shift property of
convolution states that if x1(t) * x2(t) = z(t)
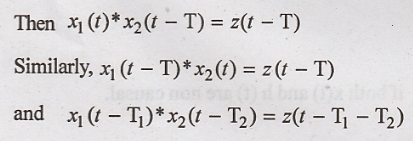
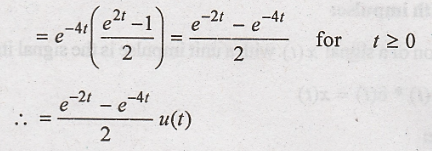
(ii) Given x1(t)
= t.u(t); x2(t) = t.u(t)
We know that 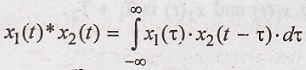
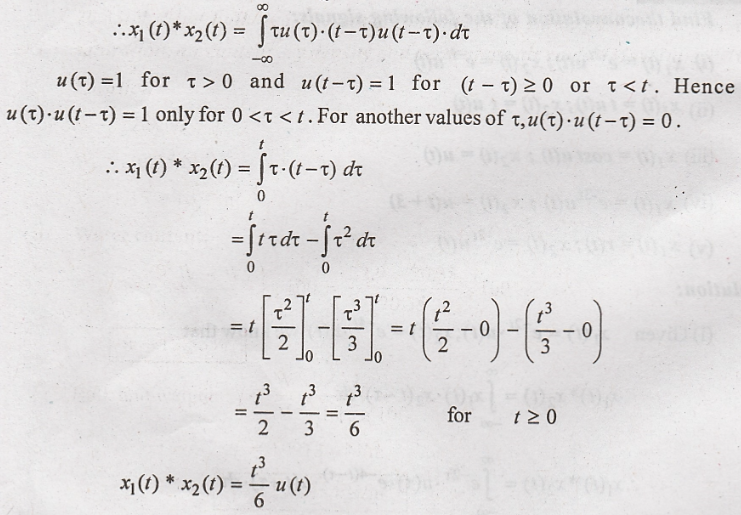
(iii) Given 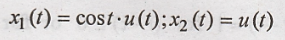
We know that
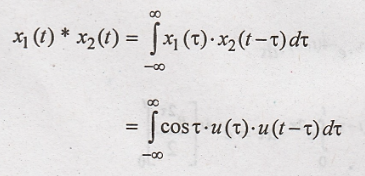
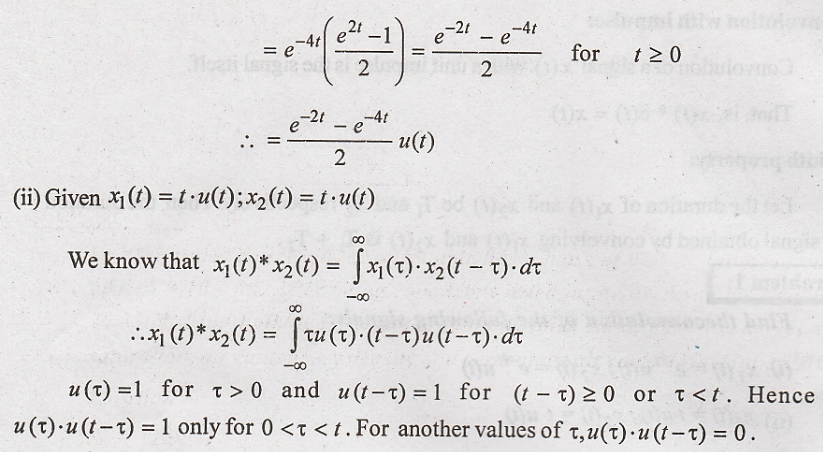

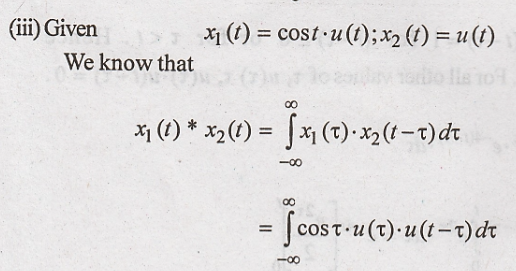
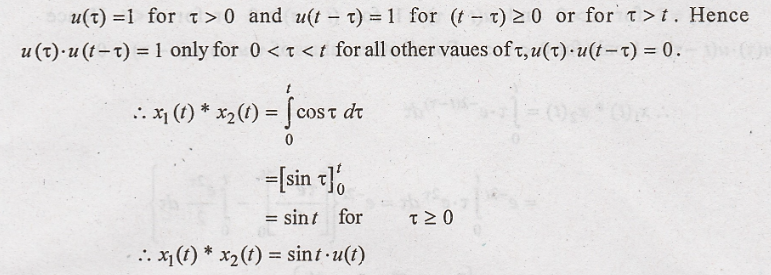
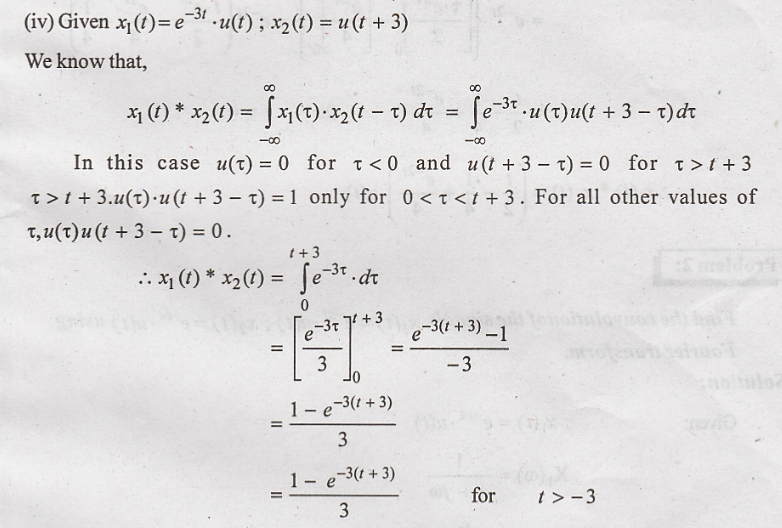
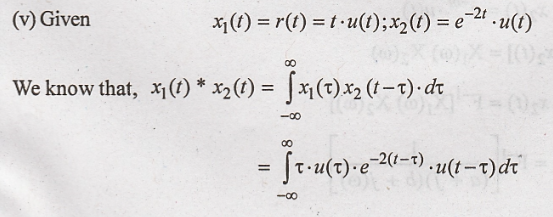
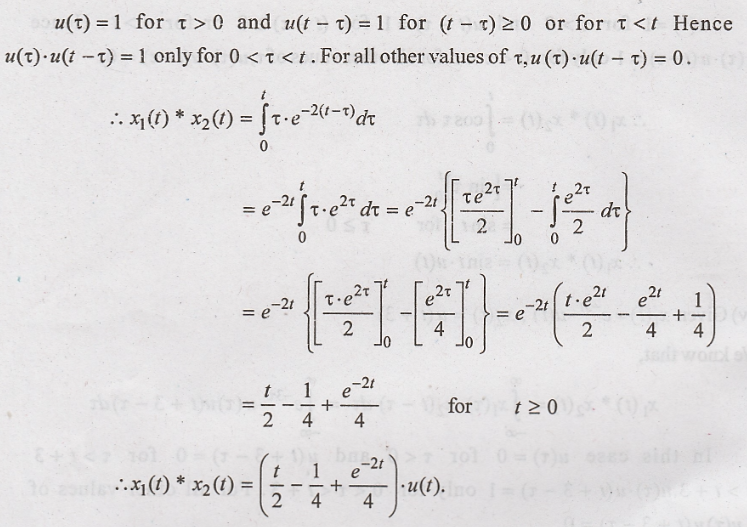
Problem 2:
Find the convolution of
the signals 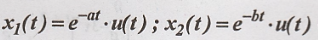 using Fourier transform.
using Fourier transform.
Solution:
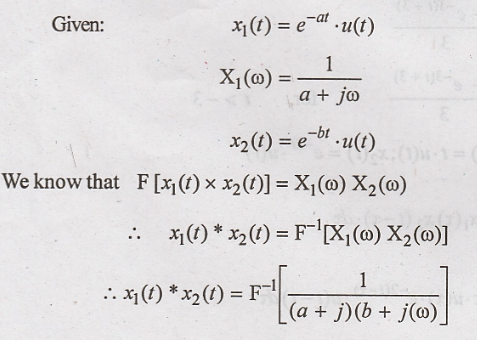
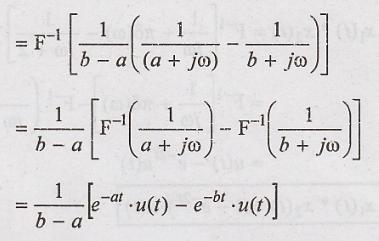
Problem 3:
Find the convolution of
the signals x1(t) = 2 e-2t u(t) and x2(t) = u(t) using
Fouier transform.
Solution:
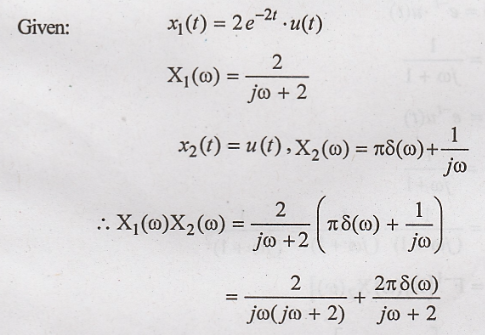
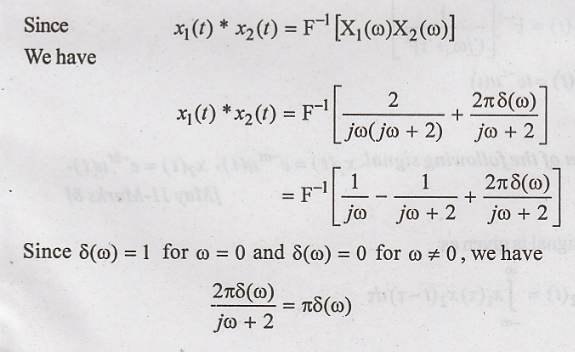
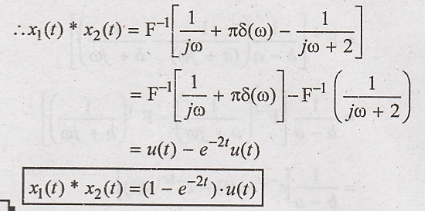
Problem 4:
Find the convolution of
signals using Fourier transform. x1(t) = et u(t) and x2(t)
= e-tu(t).
Solution:
Problem 5:
Find the convolution of
the following signal. 
Solution:
Convolution of two
signal is given as

Problem 6:
Evaluate continuous
time (CT) convolution integral given below. 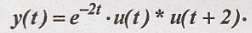 [Dec-05, May 10 -
Marks 8]
[Dec-05, May 10 -
Marks 8]
Solution:
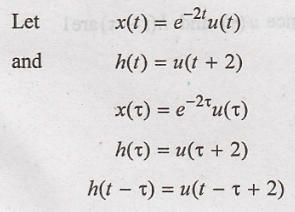
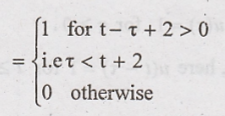
Depends upon the
overlap between x(τ) and h(t-τ) two cases are possible.
Case
I:
Figure 3.23 shows x(τ)
and h(t-τ) for different values of t. In this case there is no overlap between
x(τ) and h(t-τ). Hence products of x(τ) and h(t-τ) is zero. y(t) = 0, for t
< -2

Case
II:
Figure 3.24 shows that
there is overlap between x(τ) and h(t-τ) for t ≥ - 2. Hence convolution
becomes.
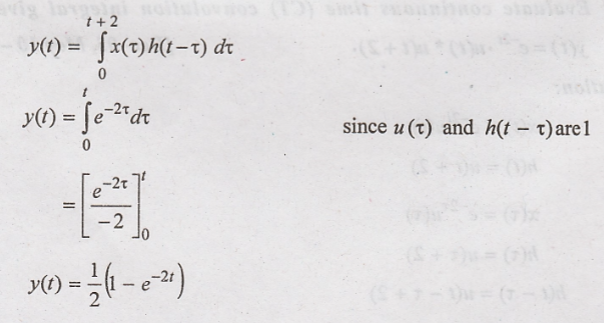
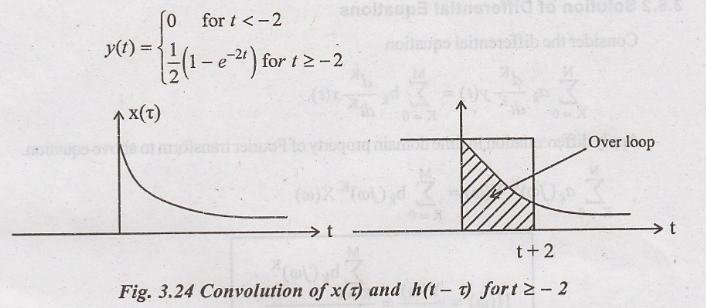
Signals and Systems: Unit III: Linear Time Invariant Continuous Time Systems,, : Tag: : Concept of convolution, Properties of Convolution - Convolution
Related Topics
Related Subjects
Signals and Systems
EC3354 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
