Random Process and Linear Algebra: Unit V: Linear Transformation and Inner Product Spaces,,
Cauchy-Schwarz inequality, Triangle inequality
Important theorems, definitions and problems
(d) Cauchy-Schwarz
inequality - Triangle inequality
Theorem :
Let V be an inner
product space over F. Then for all x, y Є V and c Є F, the following statements
are true.
(a) ||cx|| = |c|.||x||
(b) || x || = 0 if and
only if x = 0. In any case, ||x|| ≥ 0
(c) (Cauchy-Schwarz
Inequality) |(x,y)| = |x|| . || y ||
(d) (Triangle
Inequality) || x + y || ≤ ||x|| + || y ||
Proof: Let V be an
inner product space over F.
Let x,y Є V and c Є F


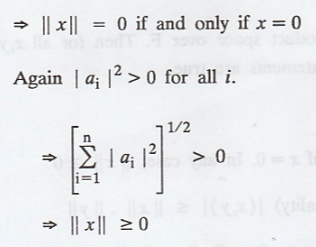
(c) If y = 0, then the
result is true.
So assume that y ≠ 0.
For any c Є F, we have
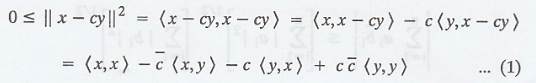
In particular,
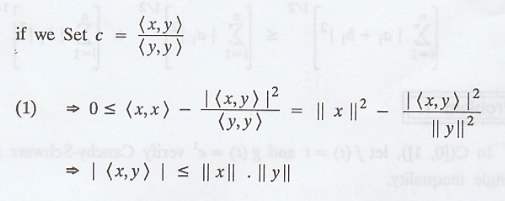
(d) We have,
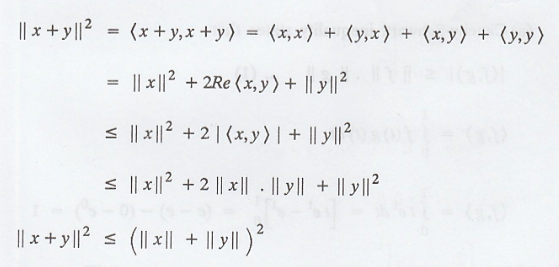
where Re<x, y>
denotes the real part of the complex number <x, y>.
=> ||x + y|| ≤ || x
|| + || y ||
Example :
For Fn, we
may apply Cauchy-Schwarz and triangle inequality to the standard inner product
to obtain the following well-known inequalities :
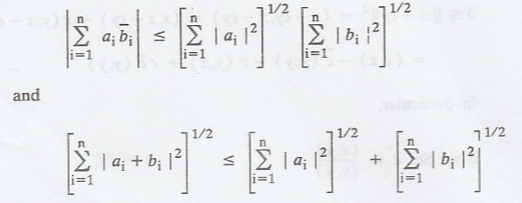
Problem 1.
In C([0, 1]), let f(t)
= t and g(t) = et verify Cauchy-Schwarz and triangle inequality.
Solution
:
(a) Cauchy-Schwarz
inequality states that
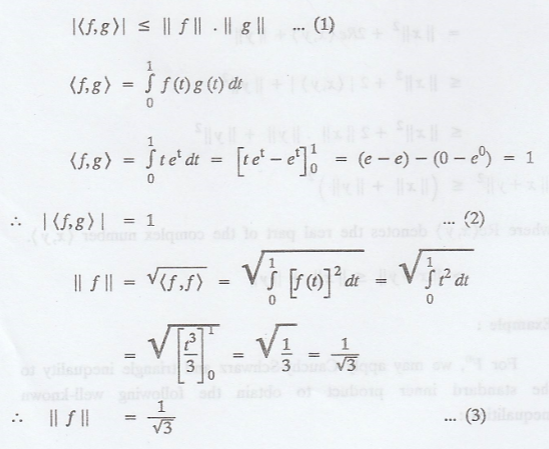
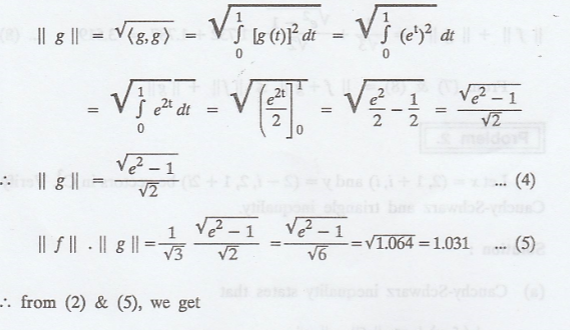
.'. from (2) & (5),
we get
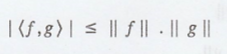
(b) Triangle inequality
states that
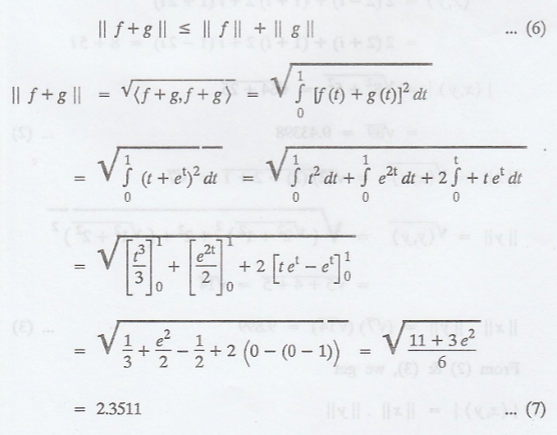
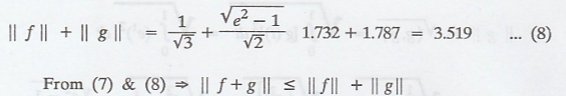
Problem 2.
Let x = (2,1 + i, i)
and y = (2-i, 2, 1+2i) be vectors in C3. Verify Cauchy-Schwarz and
triangle inequality.
Solution
:
(a) Cauchy-Schwarz
inequality states that
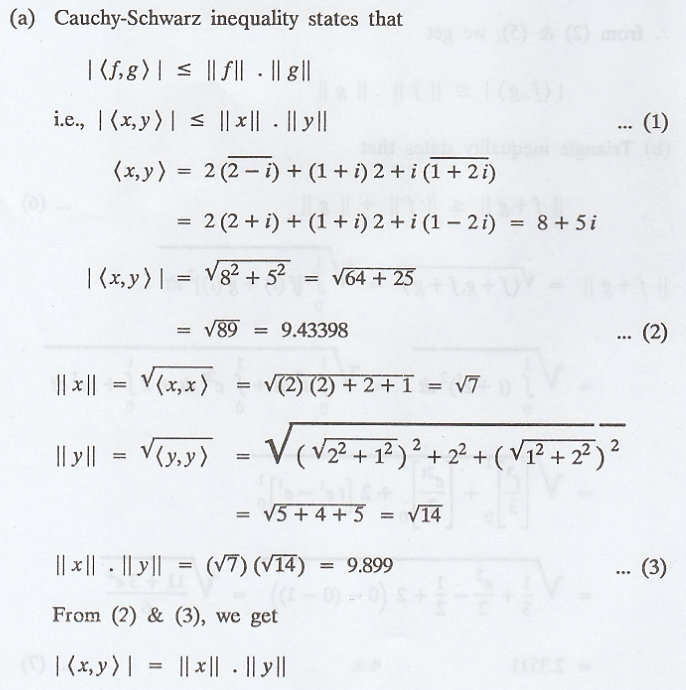
(b) Triangle inequality
states that
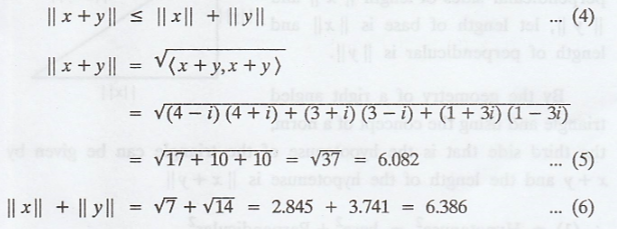
From (5), (6), we get
|| x + y || ≤ || x || +
|| y ||
Problem 3.
Let V be an inner
product space, and suppose that x and y are orthogonal vectors in V. Prove that
|| x + y ||2 = || x ||2 + || y ||2. Deduce the
Pythagorean theorem in R2.
Solution
:
x and y are orthogonal
=> <x,y> = 0
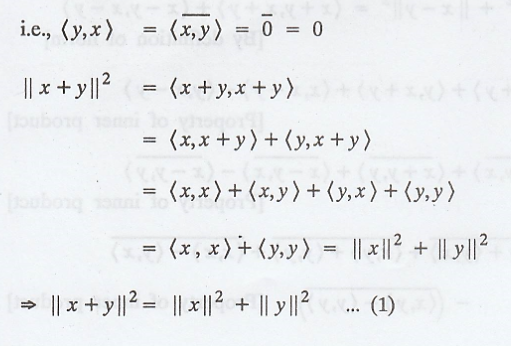
Let a right angled
triangle with perpendicular sides of length || x || and || y ||, let length of
base is ||x|| and length of perpendicular is || y ||.
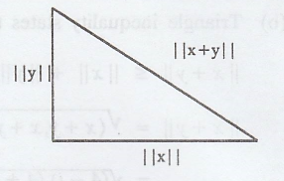
By the geometry of a
right angled triangle and using the concept of a norm, the third side that is
the hypotenuse of the triangle can be given by x + y and the length of the
hypotenuse is ||x + y||
.'. (1) ⇒ Hypotenuse2
= base2 + Perpendicular2
which is the
Pythagorean Theorem in R2
Problem 4.
Prove the parallelogram
law on an inner product space V, that is, show that
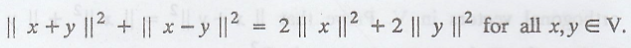
What does this equation
state about parallelograms in R2?
Solution
:
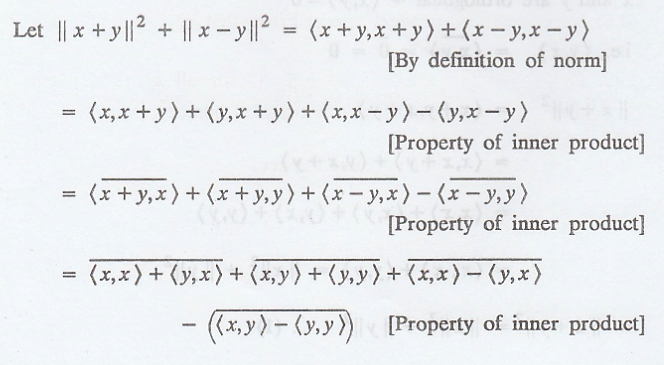
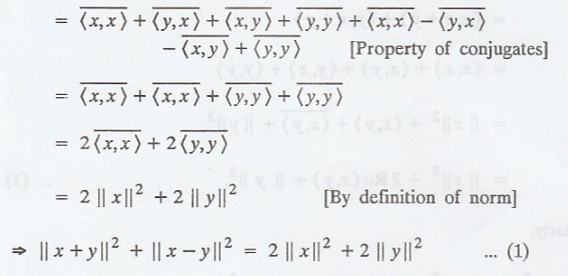
Consider a
parallelogram in R2 whose adjacent sides of length |x|| and ||y||,
then from the geometry of the parallelogram, ||x + y|| and ||x - y|| denotes
the length of two diagonals of the parallelogram.
Hence, the equation (1)
states that the sum of the area of the squares made on the diagonal of a
parallelogram is equal to twice of the sum of the area of the squares made on
the adjacent sides of the given parallelogram.
Problem 5.
Let V be an inner
product space. Prove that
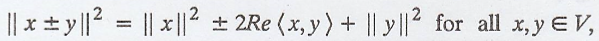 where
Re<x,y> denotes the real part of the complex number <x,y>
where
Re<x,y> denotes the real part of the complex number <x,y>
Solution:
Let V be an inner
product space.
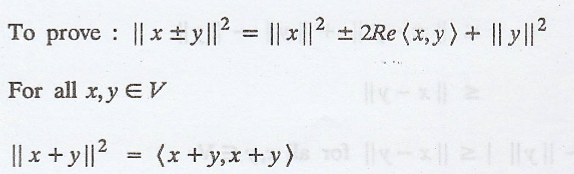
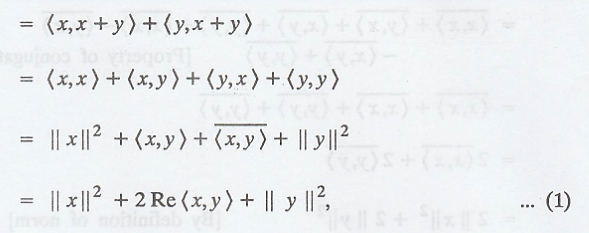
Similarly,
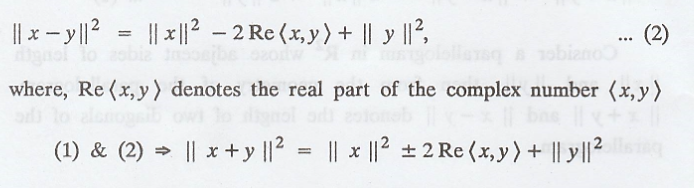
Problem 6.
Let V be an inner product space. Prove that
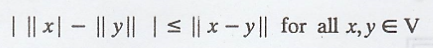
Solution
:
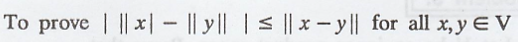
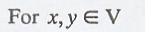
By using the traingle
inequality,
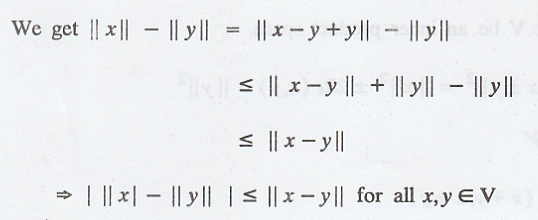
Problem 7.
Let V be an inner
product space over F. Prove the polar identities: For all x, y Є V.
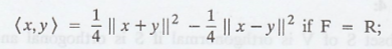
Solution
:
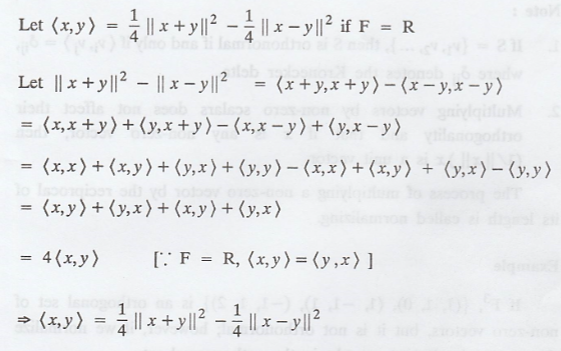
Random Process and Linear Algebra: Unit V: Linear Transformation and Inner Product Spaces,, : Tag: : - Cauchy-Schwarz inequality, Triangle inequality
Related Topics
Related Subjects
Random Process and Linear Algebra
MA3355 - M3 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
