Binomial distribution

BINOMIAL DISTRIBUTION

This distribution was discovered by James Bernoulli, though it was published in 1713, eight years after his death.

i. Bernoulli Trial

Each trial has two possible outcomes, generally called success and failure. Such a trial is known as Bernoulli trial.

The sample space for a Bernoulli trial is S = {s, f}

Example :

i. A toss of a single coin [head or tail]

ii. The throw of a die [even or odd number]

ii. Binomial experiment

An experiment consisting of a repeated number of Bernoulli trials is called Binomial experiment.

A binomial experiment must possess the following properties.

a. There must be a fixed number of trials.

b. All trials must have identical probabilities of success (p)

c. The trials must be independent of each other.

iii. Binomial distribution

Consider a set of 'n' independent Bernoullian trials (n being finite), in which the probability p of success in any trial is constant for each trial. Then q = 1 - p is the probability of failure in any trial.

A random variable X is said to follow binomial distribution if it assumes only non-negative values and its probability mass function is given by

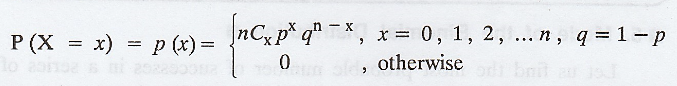
The two independent constants n and p in the distribution are known as the parameters of the distribution. 'n' is also, sometimes known as the degree of the binomial distribution.

iv. Binomial frequency distribution

Let us suppose that n trials constitute an experiment. Then if this experiment is repeated N times, the frequency function of the binomial distribution is given by, 

The expected frequencies of 0, 1, 2, ... n successes are given by the successive terms of N (q+p)ⁿ.

v. Mode of the Binomial Distribution

Let us find the most probable number of successes in a series of n independent trials with constant probability of success p i.e., we are interested in the number of successes which has the greatest probability. The probability of x successes is given by

Case 1 :

Suppose (n + 1)p is not an integer.

Let m be the integral part of (n + 1)p

But putting x = 1, 2, ... n we get

gnite P(0) < P(1) < P(2) ... < P(m) > P (m+1) > P(m+2) .... > P(n)

Therefore the greatest probability is obtained if the random variable takes the value m, the integral part of (n + 1) p

Case 2: Suppose (n + 1)p is an integer

Let (n + 1) p = m where m is an integer

Proceeding as in case 1 we get

P(0) < P(1) < ... < P(m-1) = P(m) > P (m + 1) > ... > P(m)

Therefore the greatest probability is obtained when X takes the value of m or (m-1). Hence in this case there are two modes for the binomial distribution.

vi. Additive properties of Binomial random variable

If X₁ and X₂ are two independent binomial random variables with parameters (p, n₁) and (p, n₂) then X₁ + X₂ is a binomial RV with parameters (p, n₁ + n₂).

vii. The moment generating function of a binomial distribution about the mean np

Differentiating w.r.to 't' and let t = 0, we get

Similarly, 

If X and Y are 2 independent R.Vs having the moment generating function.

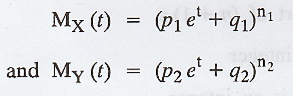
Then the moment generating function of X + Y is

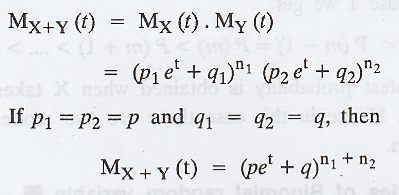
viii. The first four moments from the moment generating in M_x(pe^t+q)ⁿ

Proof :

.'. Mean = np

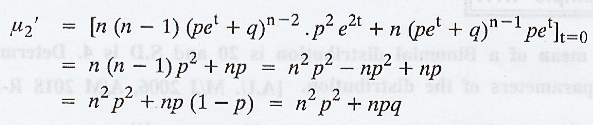
Note:

P [exactly 3] = P [equal to 3] = P[X = 3]

P [atmost 3] = P [not less than 3] = P [not more than 3] = P[X = 3]

P [atleast 3] = = P [not greater than 3] = P [not fewer than 3] = P[X = 3]

Example 1.7.1

The mean of a Binomial distribution is 20 and S.D is 4. Determine the parameters of the distribution. [A.U. M/J 2006, A/M 2018 R-13]

Solution : Given Mean = np = 20 .........(1)

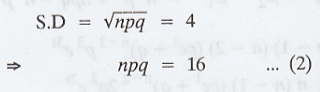
To find: n,p

The parameters of the binomial distribution are n,p

Here, n = 100, p = 1/5

Example 1.7.2

Comment on the following:

The mean of a binomial distribution is 3 and variance is 4.

Solution :

Mean = 3 and variance = 4

Which is impossible since q being a probability of an event, 0 < q < 1, But q > 1.

.'. The given data cannot determine a binomial distribution.

Example 1.7.3

In a binomial distribution consisting of 5 independent trials, probability of 1 and 2 successes are 0.4096 and 0.2048 respectively. Find the parameter P of the distribution.

Solution:

Given n = 5, P(1) = 0.4096, P(2) = 0.2048

P(x) = 

To find : p

Example 1.7.4

The mean and variance of a binomial variate are 8 and 6. Find P (X ≥ 2) [A.U_Tyli_A/M_2009]

Solution:

Given: Mean = np = 8 ............. (1)

Variance = npq = 6 ............. (2)

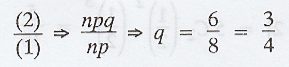
Example 1.7.5

Find the probability that in tossing a fair coin 5 times, there will appear (a) 3 heads (b) 3 tails and 2 heads (c) atleast 1 head and (d) not more than 1 tail.

Solution :

Given: p = 1/2, q = 1/2, n = 5

Let X denote number of heads

(a) P[3 heads] = P[X = 3]

(b) P [3 tails and 2 heads] = P[X = 2] 

(c) P [atleast 1 head] = P[X = 1] = 1 - P[X < 1] = 1 - P[X = 0]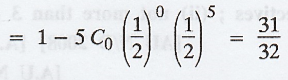 

(d) P [not more than 1 tail] = P[0 tail] + P [1 tail] = P[5 head] + P [4 head]

= P[X = 5] + P[X = 4]

Example 1.7.6

A pair of dice is thrown 4 times. If getting a doublet is considered a success, find the probability of 2 successes.

Solution :

In a throw of a pair of dice the doublets are (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) and (6, 6).

p = probability of getting a doublet = 6/36 = 1/6 and q = 1- p = 1 - 1/6 = 5/6

Probability of 2 successes = P(X = 2) 

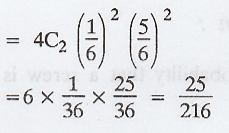
Example 1.7.7

A machine manufacturing screws is known to produce 5% defective. In a random sample of 15 screws, what is the probability that there are (i) exactly 3 defectives; (ii) not more than 3 defectives. [AU N/D 2008] [A.U CBT N/D 2011] [A.U N/D 2018 R-17 PS]

Solution:

p = probability that a screw is defective = 5/100

q = 1 - p = 1 - 5/100 = 95/100 and n = 15

Let X denote the number of defectives.

(i) P(exactly 3 defectives) = P (X = 3) 

(ii) P(not more than 3 defectives) = P(X = 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)

Example 1.7.8

If 10% of the screws produced by an automatic machine are defective, find the probability that of 20 screws selected at random, there are (i) exactly two defectives (ii) atmost three defectives (iii) atleast two defectives and (iv) between one and three defectives (inclusive) [AU Dec. 2007]

Solution :

p = Probability that a screw is defective = 10/100 = 0.1

Let X denote the number of defectives.

(i) P(exactly 2 defectives) = P(X = 2) =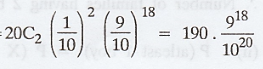 

(ii) P(atmost 3 defectives) = P(X ≤ 3) 

(iii) P (atleast 2 defectives) = P(X ≥ 2) 

(iv) Probability that the number of defectives is between one and three (inclusive)

= P (1 ≤ X ≤ 3) = P(X = 1) + P(X = 2) + P(X = 3) 

Example 1.7.9

Out of 800 families with 4 children each, how many families would be expected to have (i) 2 boys and 2 girl; (ii) atleast 1 boy; (iii) atmost 2 girls and (iv) children of both genders. Assume equal probabilities for boys and girls. [A.U M/J 2009] [A.U A/M 2019 (R17) RP]

Solution:

Considering each child is a trial, n = 4.

Assuming that birth of a boy is a success, p = 1/2 and q = 1/2

Let 'X' denote the number of successes (boys).

(i) P (2 boys and 2 girls) = P (X = 2) = 

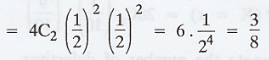
.'. Number of families having 2 boys and 2 girls = 800 × 3/8 = 300

(ii) P (atleast 1 boy) = P(X ≥ 1) = 1 - P(X < 1) = 1 - P(X = 0) 

.'. Number of families having atleast 1 boy = 800 X 15/16 = 750

(iii) P(atmost 2 girls) = P[atleast 2 boys]

= P[X ≥ 2] = 1 - P [X < 2]

= 1 - [P (X = 0) + P (X = 1)]

c

.'. Number of families having atmost 2 girls = 800 X 11/16 = 550

(iv) P(children of both genders) = 1 - P(children of the same gender)

= 1- [P(all are boys) + P(all are girls)]

= 1- [P (X = 4) + P(X = 0)]]

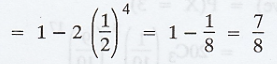
.'. The number of families having children of both gender = 800 X 7/8 = 700

Example 1.7.10

In a large consignment of electric bulb 10% are defective. A random sample of 20 is taken for inspection. Find the probability that (i) All are good bulbs (ii) Atmost there are 3 defective bulbs (iii) Exactly there are 3 defective bulbs. [A.U CBT M/J 2010] [A.U A/M 2013]

Solution:

p -> Probability that an electric bulb is defective = 1/10

q = 1 - p = 1 - 1/10 = 9/10 and n = 20

Let X denote the number of defectives.

(i) P(All are good) = P(none of them are defective) = P(X = 0)

(ii) P(Atmost three are defective) = P(X ≤ 3)

= P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)

(iii) P(Exactly 3 are defective) = P(X = 3) 

Example 1.7.11

Suppose that P (X = 0) = 1 - P(X = 1). If E(X) = 3 Var (X), find P (X = 0).

Solution :

Given P[X = 0] = 1- P[X = 1]

Given: E[X]= 3 Var[X]

Example 1.7.12

If X is a binomial random variable with expected value 6 and variance 2.4, find P (X = 5).

Solution:

We know that, E [X] = np

Var [X] = npq

Given: np = 6 ............(1)

npq = 2.4 ............(2)

Example 1.7.13

The probability of a bomb hitting a target is 1/5. Two bombs are enough to destroy a bridge. If six bombs are aimed at the bridge, find the probability that the bridge is destroyed? [AU, Dec, '98] [A.U M/J 2014]

Solution:

Let 'p' denoted the probability of a bomb hitting the target.

Given: p = 1/5; q = 1 - p = 1 - 1/5 = 4/5 and n = 6

Let X denotes the number of bombs to destroy a bridge.

the R.V X follows a binomial distribution with parameters

n = 6 & p = 1/5 and is denoted by X ~ B (n, p)

i.e., X ~ B (6, 1/5)

To find : P(X = 2)

The probability distribution is given by,

Example 1.7.14

If X follows B (3, 1/3) and Y follows B (5, 1/3) find P(X + Y = 1). [AU Dec. 2005]

Solution :

Example 1.7.15

If the m.g.f of a random variable X is of the form , what is the m.g.f of 3X + 2. Evaluate E [X].

Solution :

We know that, 

Given 

Example 1.7.16

During war, one ship out of nine was sunk on an average in making a certain voyage. What was the probability that exactly 3 out of a convoy of 6 ships would arrive safely.

Solution:

Probability (ship sinks) = p = 1/9

P(3 out of 6 ships arrive safely)

Example 1.7.17

6 dice are thrown 729 times. How many times do you expect atleast three dice to show 5 or 6 ? [A.U. N/D 2003, M/J 2004] [A.U N/D 2013] [A.U A/M 2018 R-08]

Solution :

The probability of getting 5 or 6 when a die is thrown = 2/6 = 1/3

The probability of getting atleast 3 dice to show 5 or 6 is,

= P(X ≥ 3) = P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6)

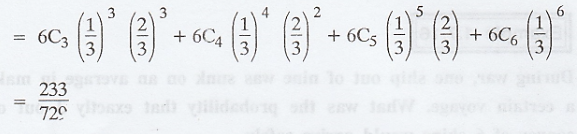
In 729 times, when 6 dice are thrown,

729 X 233/729 = 233 times

.'. In 233 times atleast 3 dice to show 5 or 6.

Example 1.7.18

The probability of a man hitting a target is 1/4. (i) If he fires 7 times, what is the probability of his hitting the target atleast twice? (ii) How many times must he fire so that the probability of hitting the target atleast once is greater than 2/3? [A.U M/J 2012, A.U A/M 2017 R13]

Solution:

Probability of hitting the target p = 1/4

q = 1 - p = 3/4

Let X denote the number of times of hitting the target. Here n = 7

By Binomial distribution, 

(i) P[hitting the target atleast twice]

= P[X ≥ 2] = 1 - P[X < 2] = 1 - [P (0) + P(1)]

(ii) P[hitting the target atleast once] = P[X ≥ 1] = 1- P[X < 1]

Example 1.7.19

A coin having probability p of coming up heads is successively flipped until the r1h head appears. Argue that X, the number of flips required will be n, n ≥ r with probability.

[A.U A/M 2010]

Solution:

A coin having probability P of coming up heads is successively flipped until rth head appears. Argue that X, the number of flips required will be n, n ≥ r with probability

This is negative Binomial distribution.

To prove the statement we first discuss Binomial distribution.

Suppose that n independent trial, each of which result in a success with probability 1-p, are to be performed.

If X represents the number of successes that occur in the n trials, then X is said to be a Binomial random variable with (n, p) is given by

In order for X, the first n - 1 flips must have r - 1 heads, and then the n^th flip must land heads.

By independent the desired probability is thus

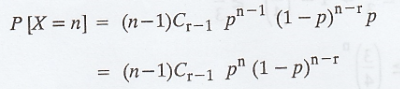
EXERCISE 1.7

1. If the chance that any one of the 10 telephone lines is busy at any instant is 0.2, what is the chance that 5 of the lines are busy? What is the probability that all the lines are busy? 

2. If 20% of the bolts produced by a machine are defective, determine the probability that out of 4 bolts chosen at random. (a) 1 (b) 0, (c) Atmost 2 bolts, will be defective. [Ans. (a) 0.4096 ; (b) 0.4096 ; (c) 0.9728]

3. If the probability that a man aged 60 will live to be 70 is 0.65, what is the probability that out of 10 men, now 60, atleast 7 will live to be 70 ? [Ans. 0.509]

4. If on the average rain falls on 10 days in every 30 days, obtain the probability that (i) rain will fall on atleast 3 days of a given week (ii) first three days of a given week will be fine and the remaining 4 days wet. [Ans. (i) 0.4294; (ii) 0.0037]

5. Fit a binomial distribution for the following data:

 [Ans. (0.432 +0.568)⁵]

6. If the probability of hitting a target is 10% and 10 shots are fired independently, what is the probability that the target will be hit atleast once? [Ans. 65 nearly]

7. Assume that half of the population is vegetarian so that the chance of an individual being a vegetarian is 1/2. Assuming that 100 investigators take samples of 10 individual each to see whether they are vegetarian, how many investigators would you expect to report that three people or less were vegetarians ? [Ans. 17]

8. In a certain town, 20% samples of the population is literate and assume that 200 investigators take samples of ten individuals to see whether they are literate. How many investigators would you expect to report that 3 people or less are literates in the samples? [Ans. 176]

9. Five fair coins are flipped. If the outcomes are assumed independent, find the probability mass function of the number of heads obtained.

10. It is known that screws produced by a certain company will be defective with probability 0.01 independently of each other. The company sells the screws in packages of 10 and offers a money-back guarantee that atmost 1 of the 10 screws is defective. What proportion of packages sold must the company replace? [Ans. 0.005]

11. Suppose that the random variable X is equal to the number of hits obtained by a certain baseball player in his next 3 bats. If P(X = 1) = 0.3, P(X = 2) = 0.2, and P(X = 0) = 3 P(X = 3).Find E (X). [Ans. 1.075]