Random Process and Linear Algebra: Unit V: Linear Transformation and Inner Product Spaces,,
Basis, N(T), R(T), Span dimension theorem
Explain about Basis, N(T), R(T), Span dimension theorem of Linear transform
(b) Basis, N(T), R(T), Span dimension theorem
Definition :
Let V and W be vector spaces, and let T: V → W be
linear. We define the null space (or kernel) N(T) of T to be the set of all
vectors x in V such that T(x) = 0; that is, N(T) = {x Є V: T(x) = 0}.
We define the range (or image) R(T) of T to be the
subset of W consisting of all images (under T) of vectors in V; that is, R(T) =
{T(x) : x ЄV}.
Example 1.
Let V and W be vector spaces, and let I : V → V and
T0: V → W be the identity and zero transformations, respectively.
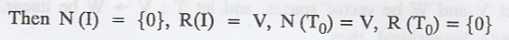
THEOREM 1.
Let V and W be vector spaces and T : V → W be
linear. Then N(T) and R(T) are subspaces of V and W, respectively.
Proof :
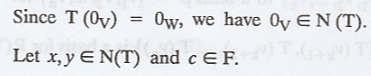

Definition :
Let V and W be vector spaces, and let T: V → W be
linear. If N(T) and R(T) are finite-dimensional, then we define the nullity of
T, denoted nullity (T), and the rank of T, denoted rank (T), to be the
dimensions of N(T) and R(T), respectively.
THEOREM 2
(Dimension Theorem) [Rank nullity theorem] :
Let V and W be vector spaces, and let T : V → W be
linear. If V is finite-dimensional, then
nullity (T) + rank (T) = dim (V)
Proof :
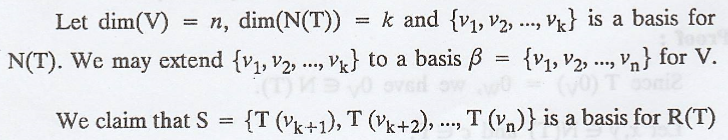
First we prove that S generates R(T). The fact that
T(vi) = 0 for 1 ≤ i ≤ k, we have
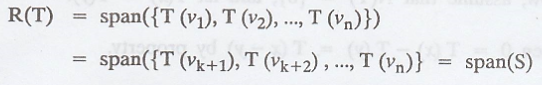
Now, we show that S is linearly independent.

Using the fact that T is linear, we have
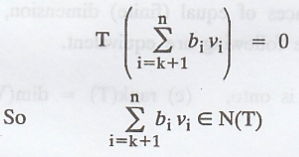
Hence, there exist c1, c2,
..., ck Є F such that

Since, β is a basis for V, we have bi = 0
for all i.
Hence, S is linearly independent.
Note: This argument also show that 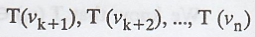 are
distinct; therefore rank(T) = n - k
are
distinct; therefore rank(T) = n - k
THEOREM 3.
Let V and W be vector spaces, and let T: V → W be
linear. Then T is one-to-one if and only if N(T) = {0}
Proof:
Let T is one-to-one and x Є N(T).
Then T(x) = 0 = T(0). Since T is one-to-one, we have
x = 0.
Hence, N(T) = {0}.
Now, assume that N(T) = {0}, and let T(x) = T(y).
Then 0 = T(x) - T(y) = T(x - y) by property.
Therefore, x - y Є N(T) = {0}. So x - y = 0, or x =
y.
This means that T is one-to-one.
THEOREM 4.
Let V and W be vector spaces of equal (finite)
dimension, and let T : V → W be linear. Then the following are equivalent.
(a) T is one-to-one, (b) T is onto, (c) rank(T) =
dim(V)
THEOREM 5.
Let V and W be vector spaces, and let T : V → W be
linear.
If β = {v1, v2, ..., vn}
is a basis for V, then

Proof :
We know that T(vi) Є R(T) for each i.
Since R(T) is a subspace, R(T) contains span 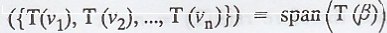
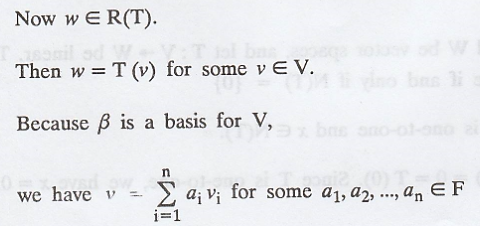
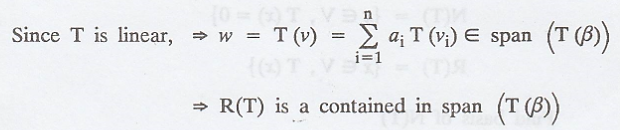
Example

Thus we have found a basis for R(T), and so dim
(R(T)) = 2
(b)(i) Basis for N(T) and compute N(T)
Problem 1.
 Find the bases for N(T) and compute
the nullity of T.
Find the bases for N(T) and compute
the nullity of T.
Solution :
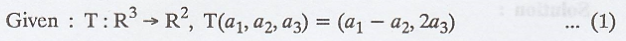
To find : N(T) and R(T)
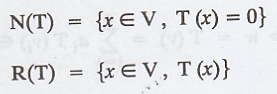
Find basis of N(T)
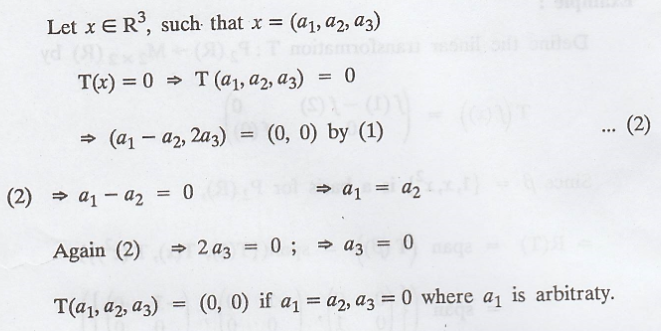
So, any element in the null space will be of the
form (a1, a2, 0)
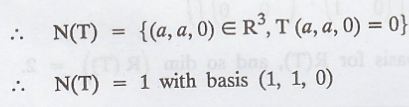
Problem 2.
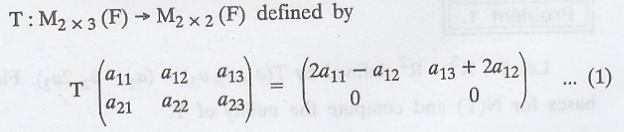
Find the basis for N(T) and compute N(T)
Solution :

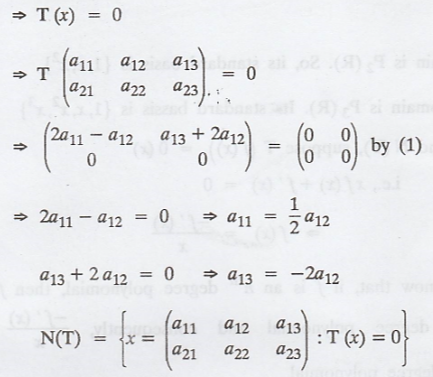
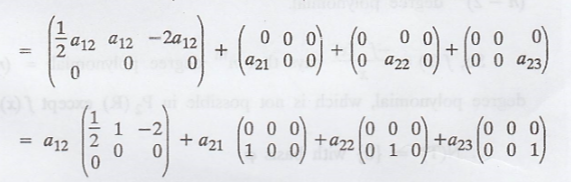
.'. N(T) is shaped by four matrices
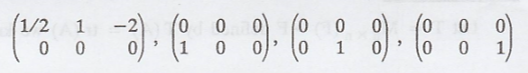
The number of basis elements of N(T) is 4.
.'. N(T) = 4
Problem 3.
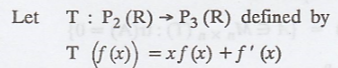
Find the basis for N(T) and compute N(T).
Solution :
Domain is P2(R). So, its standard basis
is {1, x, x2}
Co-domain is P3(R). Its standard bassis
is {1, x, x2, x3}
To find N(T), suppose T(f(x)) = 0(x)

We know that, if f is an nth degree
polynomial, then f ' is an (n-1)th degree polynomial and
consequently, -f '(x) / x is an (n-2)th degree polynomial.
Problem 4.

Find the basis for N(T) and compute N(T)
Solution :
To find the null space of T :
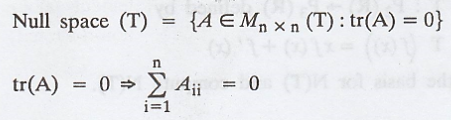
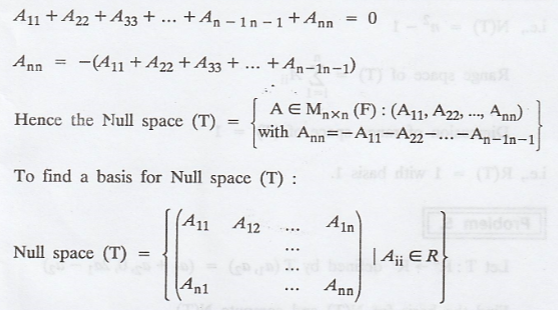
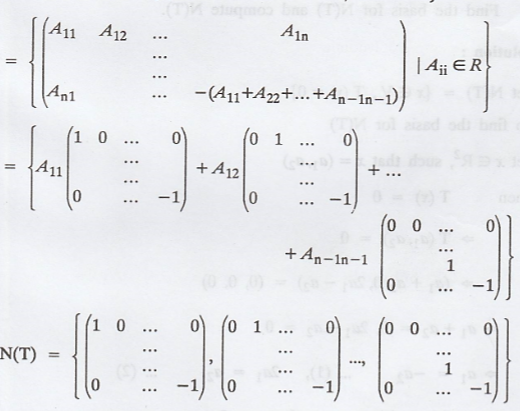
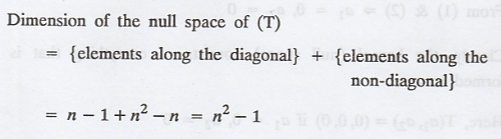
i.e., N(T) = n2 - 1
Range space of (T) = 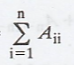
Dimension of range space of (T) = 1
i.e., R(T) = 1 with basis 1.
Problem 5.
Let T: R2 → R3 defined by T (a1,
a2) = (a1 + a2, 0, 2a1-a2)
Find the basis for N(T) and compute N(T).
Solution :
Let N(T) = {x Є V, T(x) = 0}
To find the basis for N(T)
Let x Є R2, such that x = (a1,
a2)
Then
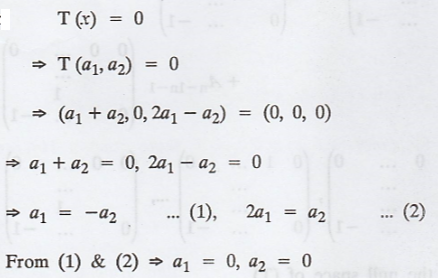
Clearly, the kernel (null space) consists of
everything that is transformed to zero.
Here, T(a1, a2) = (0, 0, 0) if
a1 = 0, a2 = 0
So, any element in the null space will be of the
form (0, 0)
In general,
N(T) = {(0, 0) Є R2: T(0, 0) = 0}
Then, the null space of T is zero dimensional.
Therefore, N(T) = 0 with basis φ
(b)(ii) Basis for R(T) and R(T)
Problem 6.
Let T: R3 → R2 defined by
T (a1, a2, a3) = (a1
- a2, 2a3)
Find the basis for R(T) and compute R(T)
Solution :
Given: T: R3 → R2
T (a1, a2, a3) = (a1-a2,
2a3)
To find a basis of range space R(T):
Clearly, for every (a, b, c) Є R3 of T,
there exists a T(a, b, c) in R2, such that,
T(a, b, c) = (a - b, 2c)
That is, any vector in R2 can be written
using the transformed elements in R3.
Suppose, (x, y) Є R2, then write (x, y) =
(a - b, 2c), where a, b and c are any real numbers.
Clearly, a - b = x have infinitely many solutions,
and assume (1/2)y = c
So,
T (a, b, c) = (a - b, 2c) = (x, y)
Then, R(T) is all of R2 or R(T) = R2
Since, {(1, 0), (0, 1)} is a standard basis for R2,
so, it is also a standard basis for R(T).
Hence, the one basis of R(T) is {(1, 0), (0, 1)} and
the rank of T is R(T) = 2
Problem 7.
Let T: R2 → R3 defined by T(a1,
a2)
= (a1 + a2, 0, 2a1
- a2)
Find the basis for R(T) and compute R(T)
Solution :
Given T: R2 → R3
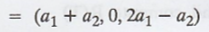
To find a basis of range space R(T):
In general, if T from V to W is a linear
transformation, and β = {v1, v2, ... vn} is a
basis for V, then
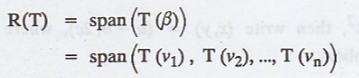
Here, β = {(1, 0), (0, 1)} is a standard basis for R3,
so,
R(T) = span (T(β))
= span (T(1, 0), T (0, 1))
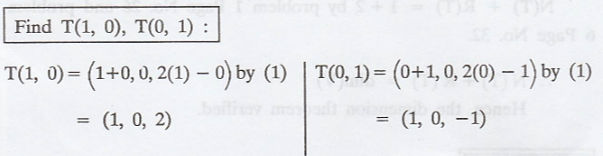
Then,

Also, clearly (1, 0, 2) and (1, 0, -1) are linearly
independent.
So, ((1, 0, 2), (1, 0, -1)} is a basis for R(T) and
the rank of T is R(T) = 2
(b) (iii) Verify the dimension theorem
Problem 8.
Verify the dimension theorem for T: R3 →
R2 defined by
T(a1, a2, a3) = (a1
- a2, 2a3)
Solution :
The dimension theorem is
If V is finite dimensional, then N(T) + R(T) =
dim(V) ... (1)
Here, R3, R2 are two vector
spaces and T : R3 → R2 is linear.
dimension of R3 is 3 dim(V) = 3
N(T) + R(T) = 1 + 2 by problem 1 Page No. 26 and
problem 6 Page No. 32.
.'. N(T) + R (T) = dim(V)
Hence, the dimension theorem verified.
Problem 9.
Verify the dimension theorem for

Solution :
The dimension theorem is
If V is finite dimensional, then N (T) + R (T) =
dim(V) ......(1)
Here, R2, R3 are two vector
spaces and T : R2 → R3 is linear
dimension of R2 is 2 => dim(V) = 2
N(T) + R(T) = 0 + 2 by problem 5 page no.31 and
problem 7 page no. 33.
.'. N(T) + R(T) = dim(V)
Hence, the dimension theorem verified.
Problem 10.
Verify the dimension theorem for

Solution :
The dimension theorem is
If V is finite dimensional, then N (T) + R (T) =
dim(V) ... (1)
Here, M2 x 3(F) and M2 x 2(F)
are two vector spaces and

N(T) + R(T) = 4 + 2 by problem 2 and problem 3
.'. N(T) + R(T) = dim(V)
Hence, the dimension theorem verified.
Problem 11
Verify the dimension theorem for
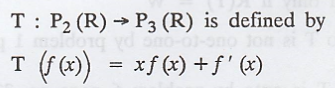
Solution :
The dimension theorem is
If V is finite dimensional, then N(T) + R(T) =
dim(V) ...... (1)
Here, P2(R), P3(R) are two
vector spaces and animals
T : P2(R) → P3(R) is linear.
dim [P2(R)] = 3
N(T) + R(T) = 0 + 3 = 3 by problem 3 & Problem 9
.'. N(T) + R(T) = dim(V)
Hence, the dimension theorem verified.
(b) (iv) Determine T is one-to-one or onto V
Problem 12
Determine T is one-to-one or onto for T : R3
→ R2 defined by
T(a1, a2, a3) = (a1
- a2, 2a3)
Solution :
To determine whether the given transformation is
one-to-one or onto.
In general, if T : V → W a linear transformation,
and N(T), and R(T) are null space and range of T, then
1. T is one-to-one if and only if N(T) = 0
2. T is onto if and only if R(T) = W
Here, N(T) = 1, so T is not one-to-one by problem 1
And R(T) = 2, so T is onto by problem 6
Therefore, the given transformation is onto, but not
one-to-one
Problem 13.
Determine T is one-to-one or onto for T: R2
→ R3 defined by
T(a1, a2) = (a1 + a2,
0, 2a1-a2)
Solution :
To determine whether the given transformation is
one-to-one or onto.
In general, if T : V → W a linear transformation,
and N(T), and R(T) are null space and range of T, then,
1. T is one-to-one if and only if N(T) = 0
2. T is onto if and only if R(T) = W
Here, N(T) = 0, so T is not one-to-one by problem 5
page no.31
Clearly, T is not onto, because, T will never map
all of R3.
For example T will never map (1, 1, 1).
Also,
rank (T) ≠ dim (R3)
2 ≠ 3
Therefore, the given transformation T is one-to-one,
but not onto
Problem 14.
Determine T is one-to-one or onto
T: M2 x 3(F) → M2 x 2(F)
defined by

Solution :
We know that, a linear mapping T : V → W is
one-to-one if and only if N(T) = {0}
Since N(T) ≠ {0}, therefore T is not one-to-one.
Since, rank(T) = 2 and dim (M2 x 3(F)) =
4, that is
rank(T) ≠ dim (M2
× 3(V)}
therefore T is not onto by problem 2 & 8.
Hence, T is neither one-to-one nor onto.
Problem 15.
Determine T is one-to-one or onto T: P2(R)
→ P3(R) defined by
T(f(x)) = x f(x) + f'(x)
Solution :
We know that the dimension of domain P2(R)
< dimension of the co-domain P3(R)
From this, the linear transformation T is not onto.
Theorem :
Let V and W be vector spaces, and let T : V → W be
linear. Then T is one-to-one if and only if N(T) = {0}
Here, we have N(T) = {0}
So, the above theorem confirms that T(f(x)) = x f(x)
+ ƒ'(x) is a one-to-one function.
Problem 16.
Give an example of a linear transformation T: R2
→ R2 such that N(T) = R(T)
Solution :
Consider the linear transformation T : R2
→ R2
Construct an example, such that N(T) = R(T)
Take T(x, y) = (y, 0)
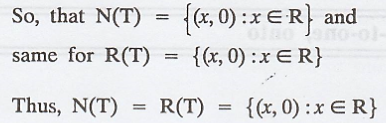
Problem 17.
Give an example of distinct linear transformations T
and U such that N(T) = N(U) and R(T) = R(U)
Solution :
Let the linear transformations; T and U
Let T : R → R, defined by T(x) = 2x
And also U : R → R is defined by U(x) = x
The nullity of T is the set of all vectors x in R.
Such that T(x) = 0
Similarly, for the transformation U.
So, that N(T) = {0} and N(U) = {0}
⇒
N(T) = N(U) = {0}
The range of T or U is a subset of co-domain
consisting of all images
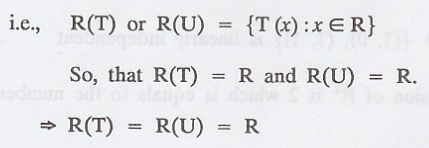
Random Process and Linear Algebra: Unit V: Linear Transformation and Inner Product Spaces,, : Tag: : - Basis, N(T), R(T), Span dimension theorem
Related Topics
Related Subjects
Random Process and Linear Algebra
MA3355 - M3 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
