Bases and Dimension

BASES AND DIMENSION

Definition :

A basis β for a vector space V is a linearly independent subset of V that generates V.

If β is a basis for V, we also say that the vectors of β form a basis for V.

(or)

A set S = {u₁, u₂, ..., u_n} of vectors is a basis of V if it has the following two properties.

(1) S is linearly independent.

(2) L(S) = V, i.e., every element of V is a linear combination of finite elements of S.

Example 1.

Recalling that span(Ø) = {0} and Ø is linearly independent, we see that Ø is a basis for the zero vector space.

Example 2.

Example 3.

Example 4.

In P_n(F) the set {1, x, x²,..., xⁿ) is a basis. We call this basis is the standard basis for P_n (F).

Example 5.

In P(F) the set {1, x, x²,...} is a basis.

THEOREM 1.

Let V be a vector space and β = {u₁, u₂, ..., u_n} be a subset of V. Then β is a basis for V if and only if each v ε V can be uniquely expressed as a linear combination of vectors of β, that is, can be expressed in the form.

for unique scalars a₁, a₂, ..., a_n

Proof :

Let β be a basis for V.

If v ε V, then v ε span(β) because span(β) = V.

Thus v is a linear combination of the vectors of β.

Suppose that

are two such representions of v.

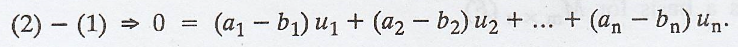
Since β is linearly independent, it follows that

Hence a₁ = b₁, a₂ = b₂, = ... = a_n = b_n, and so v is uniquely expressible as a linear combination of the vectors of β.

Converse part:

Suppose every vector, v ε V can be written as a linear combination of vectors of β = {u₁, u₂, ..., u_n} in a unique way.

To prove that β = {u₁, u₂, ..., u_n} is the basis of V.

Since every vector v ε V can be written as a linear combination of β, confirm that β spans V.

Now, prove that β is linearly independent.

Suppose, 

Since 0 vector is always linearly dependent and cannot span any vector, say that β is the non-zero set of vectors.

Since β is a subset of V, say that any vector in β also can be written as a linear combination of vectors of β.

=> Some vector u_i can be written as a linear combination of its preceeding vectors.

i.e., u_k, u_k+1, ..., u_n are dependent and so, they can be written as linear combinations of the preceeding vectors.

Neglecting these vectors from β, we are left with {u₁, u₂, ..., u_n}, such that these vectors span V.

If these vectors are linearly independent, then they form the basis to V.

Otherwise, some vector ui is a linear combination of its preceeding vectors.

So, omitting that vector, only the subset is left {u₁, u₂, ..., u_i-1, u_j+1,..., u_k), such that these vectors span V and are linearly independent.

Thus, this set forms a basis to V.

Hence, the theorem.

THEOREM 2.

If a vector space V is generated by a finite set S, then some subset of S is a basis for V. Hence V has a finite basis.

Proof :

If S = Ø or S = {0}, then V = {0} and is a subset of S that is a basis for V.

Otherwise S contains a non-zero vector u1.

{u₁} is a linearly independent set. Continue, if possible, choosing u₂, ..., u_k in S such that {u₁, u₂, ..., u_k} is linearly independent.

Since S is a finite set, we must eventually reach a stage at which β = {u₁, u₂, ..., u_k} is a linearly independent subset of S, but adjoining to β any vector in S not in β produces a linearly dependent set.

We claim that β is a basis for V. Because β is linearly independent by construction, it suffices to prove that β spans V.

To show that S  span (β).

THEOREM 3. Replacement theorem

Let V be a vector space that is generated by a set G containing exactly n vectors, and let L be a linearly independent subset of V containing exactly m vectors. Then m ≤ n and there exists a subset H of G containing exactly n - m vectors such that L U H generates V.

Proof :

The proof is by mathematical induction on m.

For m = 0, we get L = Ø and H = G

For m ≥ 0, assume that the theorem is true.

To prove the theorem is true for m + 1 also.

Note n - m > 0, lest v_m+1 be a linear combination of v₁, v₂, ..., v_m, which contradicts the assumption that L is linearly independent.

Hence n > m; that is n ≥ m + 1.

Moreover, some b_i, say b₁, is non-zero, for otherwise we obtain the same contradiction.

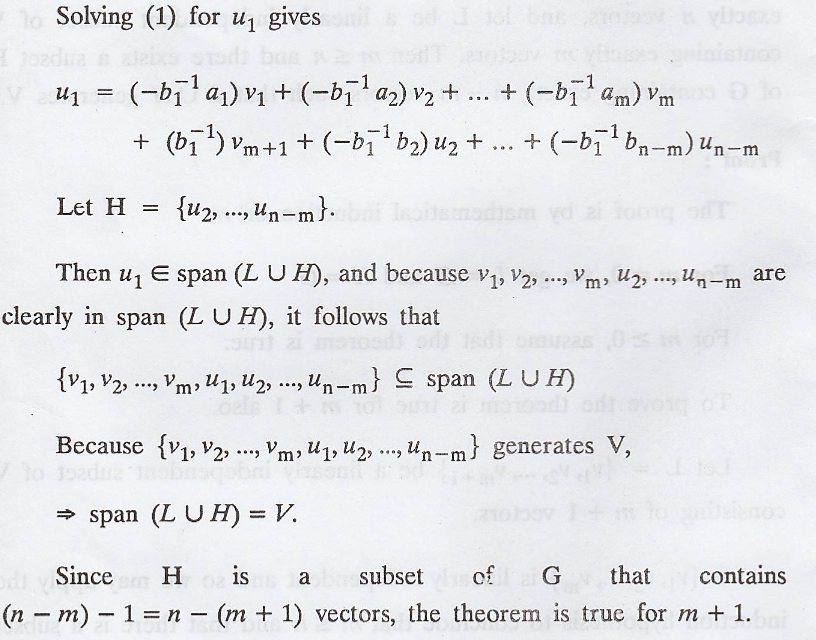
This completes the induction.

Hence, proved.

THEOREM 4.

Let V be a vector space having a finite basis. Then every basis for V contains the same number of vectors.

Proof :

Suppose that β is a finite basis for V that contains exactly n vectors, and let γ be any other basis for V.

If γ contains more than n vectors, then we can select a subset S of γ containing exactly n + 1 vectors.

Since S is linearly independent and β generates V, the replacement theorem implies that n + 1 ≤ n, a contradiction.

Therefore γ is finite, and the number m of vectors in y satisfies

Reversing the role of β and γ, we obtain n ≤ m.

Hence, m = n.

Definition :

A vector space is called finite-dimensional if it has a basis consisting of a finite number of vectors. The unique number of vectors in each basis for V is called the dimension of V and is denoted by dim(V). A vector space that is not finite-dimensional is called infinite-dimensional.

Example 1.

The vector space {0} has dimension zero.

Example 2.

The vector space Fⁿ has dimension n.

Example 3.

The vector space M_{m x n}(F) has dimension m n.

Example 4.

The vector space P_n(F) has dimension n + 1

Example 5.

Over the field of complex numbers, the vector space of complex numbers has dimension 1. (A basis is {1}).

Example 6.

Over the field of real numbers, the vector space of complex numbers has dimension 2. (A basis is {1, i}).

THEOREM 5.

Let V be a vector space with dimension n.

(a) Any finite generating set for V contains atleast n vectors, and a generating set for V that contain exactly n vectors is a basis for V.

(b) Any linearly independent subset of V that contains exactly n vectors is a basis for V.

(c) Every linearly independent of V can be extended to a basis for V.

Proof :

Let β be a basis for V.

(a) Let G be a finite generating set for V.

→ Some subset H of G is a basis for V.

→ H contains exactly n vectors.

Since subset of G contains n vectors, G must contain atleast n vectors.

Moreover, if G contains exactly n vectors, then we must have H = G, so that G is a basis for V.

(b) Let L be a linearly independent subset of V containing exactly n vectors.

By the replacement theorem that there is a subset H of β containing n - n = 0 vectors such that L U H generates V.

Thus H = Ø, and L generates V.

Since L is also linearly independent, L is a basis for V.

(c) If L is a linearly independent subset of V containing m vectors, then the replacement theorem asserts that there is a subset H of β containing exactly n - m vectors such that L U H generates V. Now L U H contains at most n vectors; therefore (a) implies that L U H contains exactly n vectors and that L U H is a basis for V.

THEOREM 6.

Let W be a subspace of a finite-dimensional vector space V. Then W is finite-dimensional and dim(W) ≤ dim(V). Moreover, if dim(W) = dim(V), then V = W.

Proof :

Let dim(V) = n.

If W = {0}, then W is finite-dimensional and dim(W) = 0 ≤ n.

Otherwise, W contains a non-zero vector x₁; so {x₁} is a linearly independent set.

Continue choosing vectors, x₁, x₂,...,x_k in W such that {x₁, x₂, ..., x_k} is linearly independent.

Since no linearly independent subset of V can contain more than n vectors, this process must stop at a stage where k ≤ n and {x₁, x₂,..., x_k} is linearly independent but adjoining any other vector from W produces a linearly dependent set.

.'. {x₁, x₂,...,x_k} generates W, and hence it is a basis for W. Therefore dim(W) = k ≤ n.

If dim(W) = n, then a basis for W is a linearly independent subset of V containing n vectors. But the replacement theorem implies that this basis for W is also a basis for V; so W = V.

Example 1.

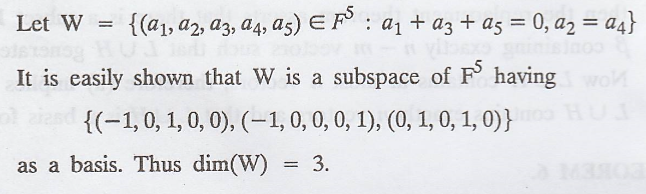
Example 2.

The set of diagonal n x n matrices is a subspace W of M_{n x n}(F). A basis for W is

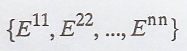
where E_ij is the matrix in which the only non-zero entry is a one in the i^th row and j^th column. Thus dim(W) = n.

Example 3.

The set of symmetric n x n matrices is a subspace W of M_{n x n}(F). A basis for W is

where A^ij is the n x n matrix having 1 in the i^th row and j^th column, 1 in the j^th row and i^th column, and 0 elsewhere. It follows that

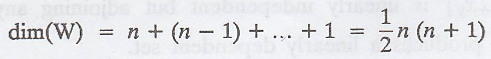
THEOREM 7.

If W is a subspace of a finite-dimensional vector space V, then any basis for W can be extended to a basis for V.

Proof :

Let S be a basis for W. Because, S is a linearly independent subset of V. The replacement theorem guarantees that S can be extended to a basis for V.

Example 1.

The set of all polynomials of the form

(a) Vector space

Problem 1.

Give three different bases for F² and for M_{2 x 2}(F)

Solution :

We know that F² is of dimension 2.

So, any set of two linearly independent vectors form a basis of F².

(i) The standard basis is {(1, 0), (0, 1)}

(ii) Let S = {(1, 1), (2, 1)}

To prove that S is a basis to F²

Let a (1, 1) + b (2, 1) = (0, 0)

a + 2b = 0 ........(1)

a + b = 0 ........ (2)

Solving (1) & (2) we get a = 0, b = 0

.'. S is linearly independent

⇒ S is a basis to F²

(iii) Let S = {(2, 0), (0, 2)}

We can easily verify, S is basis to F²

M_{2 x 2} is a vector space of dimension 4.

So, we consider a subset of M_{2 x 2} with dimension 4 and show that the set is linearly independent and claim that the set forms a basis to M_{2 x 2}

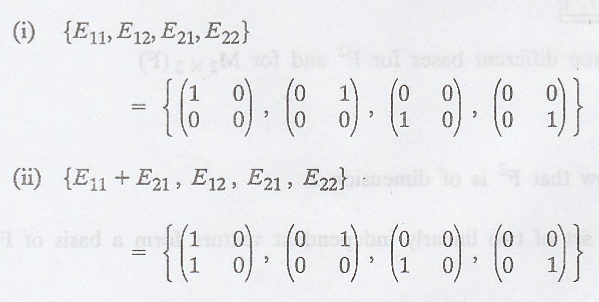
Problem 2

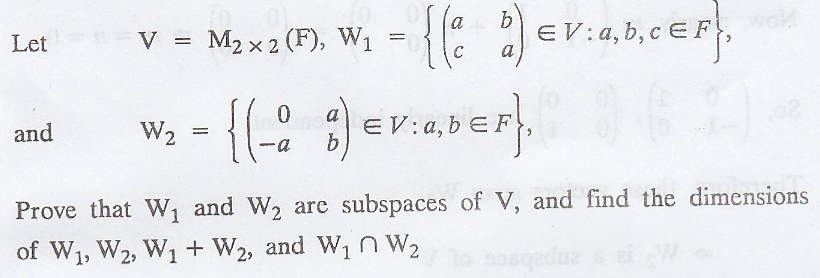
Solution :

(b) To prove W₂ is a subspace of V also find the dim(W₂)

Therefore, these vectors span W₂

⇒ W₂ is a subspace of V

Therefore, dim W₂ = 2

(c) To find the dim(W₁+W₂) and dim(W₁ ∩ W₂)

Collecting all the bases vectors of W₁ and W₂.

Therefore, the dim(W₁ ∩ W₂)

So, by the theorem

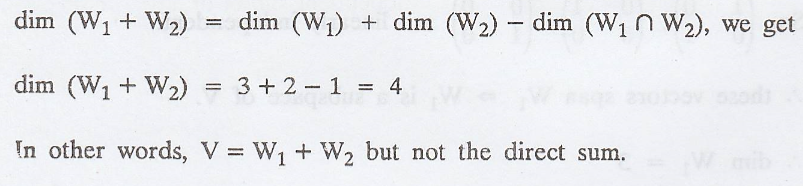
(b) Problems on Vector space kⁿ, Pⁿ(t), Bases.

Problem 1.

Determine which of the following sets are bases for R³

{(1, 0, -1), (2, 5, 1), (0, -4, 3)}

Solution :

{(1, 0, -1), (2, 5, 1), (0, -4, 3)}

It is to determine that the set is bases for R³

i.e., To find that is linearly independent or linearly dependent.

Suppose that a₁, a₂, a₃ are scalars such that

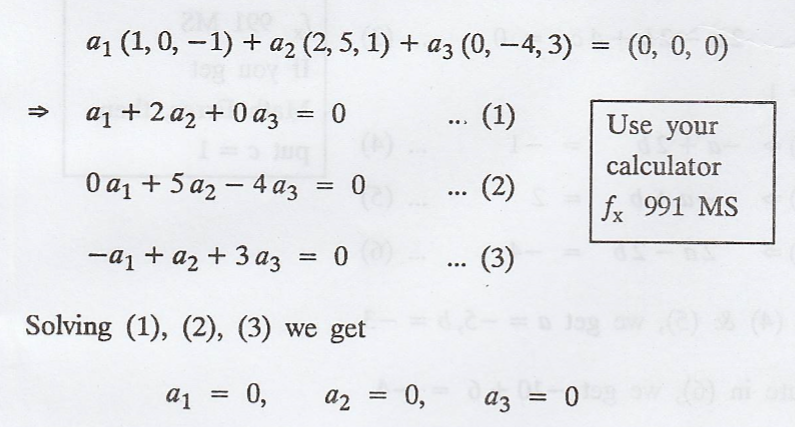
=> The set is linearly independent.

And by the theorem "Any linearly independent subset of V that contains exactly n vectors is a basis for V."

Hence, given set is basis for R³.

Problem 2.

Determine which of the following set are bases for P₂(R)

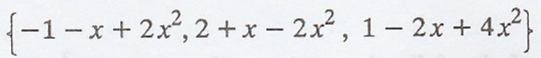
Solution :

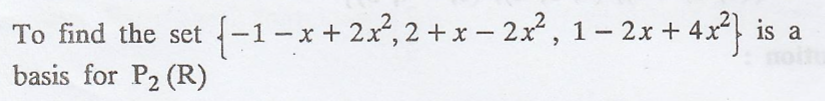
First find the set is linearly independent or not.

It is clear that c is arbitrary. So the given set is linearly dependent.

Then

The matrix of the above system of equations is as follows:

Problem 3.

Do the polynomials x³ - 2x + 1, 4x² - x + 3, and 3x - 2 generate P₃(R)? Justify your answer.

Solution :

Given: x³ - 2x + 1, 4x² - x + 3, 3x - 2

Here, P₃(R) consist of all polynomials having degree less than or equal to 3.

Clearly, the given three polynomials are belongs to P₃(R)

In general, the vector space P_n(R) has a dimension n + 1.

So, the vector space P₃(R) has diameter 3 + 1 = 4

i.e., the unique number of vectors in each basis of P₃(R) is 4.

So, the given three polynomials cannot span entire space.

Therefore, the given polynomials cannot generate P₃(R).

Problem 4.

Is {(1, 4, -6), (1, 5, 8), (2, 1, 1), (0, 1, 0)} a linearly independent subset of R³? Justify your answer.

Solution :

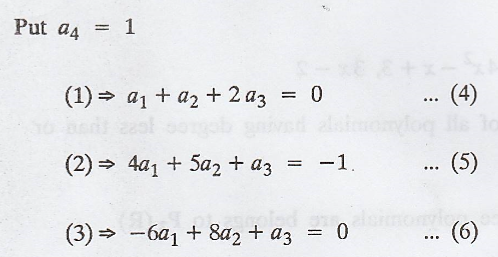
Solve by using your calculator f_x991MS we get

It is clear that a₄ is arbitrary.

Hence, the given set of vectors are linearly dependent.

Problem 5.

Let W denote the subspace of R⁵ consisting of all the vectors having co-ordinates that sum to zero.

The vectors

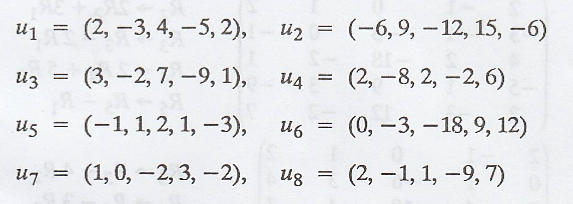
generate W. Find a subset of the set {u₁, u₂, ..., u₃} that is a basis for W.

Solution :

Let us consider

In matrix notation, we get

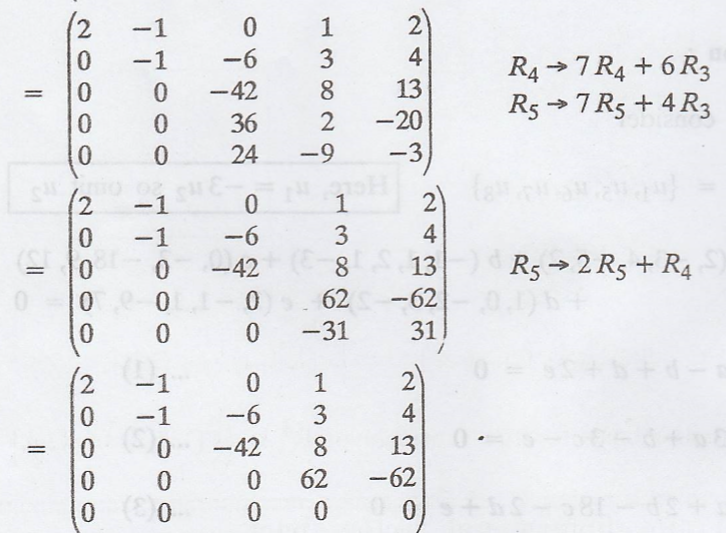
The row with all entries 0 can be omitted.

Problem 6.

The set of solutions to the system of linear equations

is a subspace of R³. Find a basis for this subspace.

Solution:

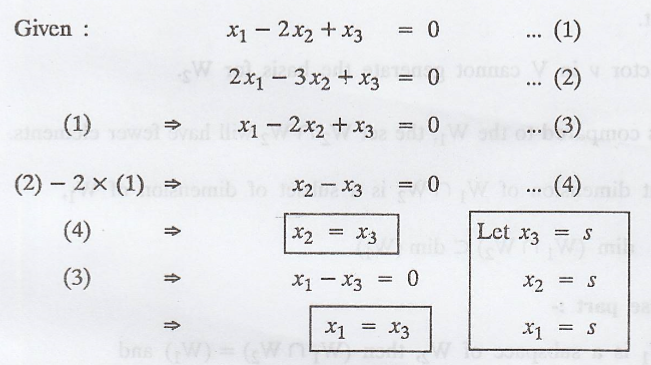
(c) Finite dimensional vector space

Problem 1.

Let W₁ and W₂ be subspaces of a finite-dimensional vector space V. Determine necessary and sufficient conditions on W₁ and W₂ so that dim (W₁ ∩ W₂) = dim (W₁).

Solution :

Let W₁ and W₂ be the two subspaces and let W₁ C W₂

Let α and β as the basis for W₁ and W₂ respectively and they are finite.

Let us prove this by the method of contradiction.

Suppose W₁ is not a subspace of W₂, then there will be no common element.

The vector v in V cannot generate the basis for W₂.

Now as compared to the W₁, the set W₂ ∩ W₂ will have fewer elements.

So, that dimension of W₁ ∩ W₂ is a subset of dimension of W₁,

that is dim (W₁ ∩ W₂) C dim (W₁)

Converse part :-

Let W₁ is a subspace of W₂, then (W₁ ∩ W₂) = (W₁) and W₂ is a subspace of W₁, then (W₁ ∩ W₂) = (W₂)

So, that W₁ ∩ W₂ contains same vectors as that of W₁.

Hence, the statement can be written as

dim (W₁ ∩ W₂) = dim (W₁)

i.e., both subspaces have same dimension.

Problem 2.

Let W₁ and W₂ be the subspaces of P(F). Determine the dimensions of the subspaces W₁ ∩ P_n(F) and W₂ ∩ P_n(F)

Solution :

Proof: Let the subspaces of vector space V: W₁, W₂ and polynomial P_n(F).

W₁ is a subspace of all polynomials f(x) in P_n(F), represents as

Similarly, W₂ is a subspace of all polynomials g(x) in P_n(F), represents as

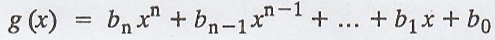
If n is odd, then

and if n is even, then

(d) Sum and direct sum of subspaces

Problem 1.

Let W₁ and W₂ be subspaces of a vector space V having dimensions m and n, respectively, where m ≥ n.

(a) Prove that dim (W₁ ∩ W₂) ≤ n

(b) Prove that dim (W₁+ W₂) ≤ m + n

Solution :

Let W₁ and W₂ are two subspaces of finite dimensional vector space V.

dim (W₁) = m and dim (W₂) = n

(a) 

Take dimension on both sides

dim (W₁ ∩ W₂) ≤ dim (W₂)

dim (W₁ ∩ W₂) ≤ n

Hence, dim (W₁ ∩ W₂) ≤ n.

(b) Let the expression for dim (W₁ + W₂)

Problem 2.

(a) Find an example of subspaces W₁ and W₂ of R³ with dimensions m and n, where m > n > 0, such that dim (W₁ ∩ W₂) = n.

(b) Find an example of subspaces W₁ and W₂ or R³ with dimensions m and n, where m > n > 0, such that dim (W₁ + W₂) = m + n.

(c) Find an example of subspaces W₁ and W₂ of R³ with dimensions m and n, where m ≥ n, such that both dim (W₁ ∩ W₂) < n and dim (W₁ + W₂) < m + n.

Solution:

 

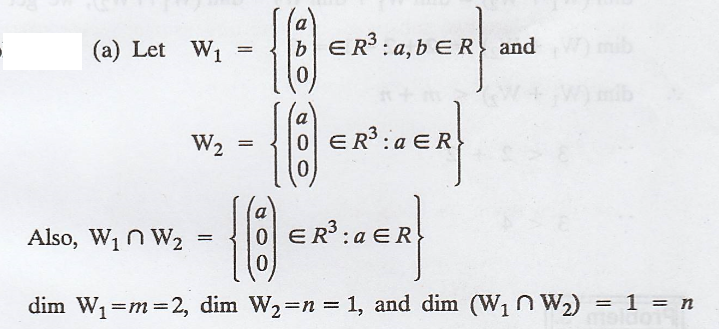
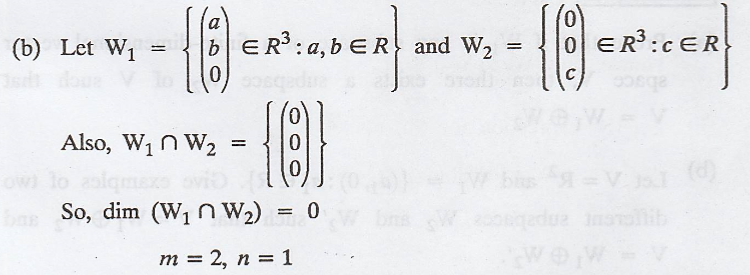
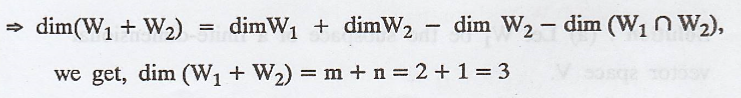
Using these observations in

Problem 3.

(a) Prove that if W₁ is any subspace of a finite-dimensional vector space V, then there exists a subspace W₂ of V such that

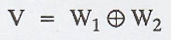
Solution:

(a) Let W₁ be the subspace of a finite-dimensional vector space V.

That is to prove that there exists a subspace W₂ of V such that 

Let α be the basis of V and β be the basis of W₁.

The basis β can be extended to β' by using the Replacement Theorem.

Hence, there exists a subspace W₂ of V such that 

(b) 

That is to give examples of two different subspaces W₂ and W₂' such that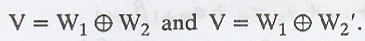 

If the vector space V = R², then obviously, the different subspaces of V are W₂ and W₂'.

Problem 4.

Let W be a subspace of a finite-dimensional vector space V, and consider the basis {u₁, u₂, ..., u_k} for W. Let {u₁, u₂, ..., u_k, u_k+1, ..., u_n} be an extension of this basis to a basis for V.

(a) Prove that 

(b) Derive a formula relating dim(V), dim(W), and dim(V/W).

Solution:

Let S = {α₁, α₂, ..., α_m} be a basis of W.

As S is linearly independent, then S can be extended to form basis of V.

Let the set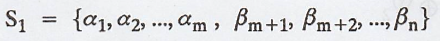 

Then, dim(V) = m + n

By the definition of Quotient space.

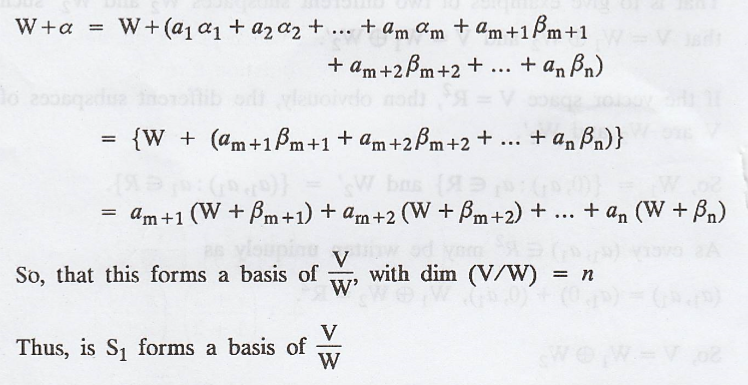
(b) Let the subspace W of V, with dimension of W is m and dimension of V is m + n.

The relation can be formulated as follows.

(e) Lagrange interpolation formula

Problem 1.

In each part, use the Lagrange interpolation formula to construct the polynomial of smallest degree whose graph contains the following points.

(a) (-2, -6), (-1, 5), (1, 3)

(b) (-4, 24), (1, 9), (3, 3)

Solution :

To find the polynomial of smallest degree which passes through a given set of points we may use Lagrange's interpolation formula which states.

EXERCISE 4.5

1. Determine which of the following sets are bases for R³

(a) {(2, -4, 1), (0, 3, -1), (6, 0, -1)}

(b) {(1, 2, -1), (1, 0, 2), (2, 1, 1)}

(c) {(-1, 3, 1), (2, -4, -3), (-3, 8, 2)}

(d) {(1, 0, -1), (1, 2, 1), (0, -3, 2)}

(e) {(1, 2, 1), (2, 9, 0), (3, 3, 4)}

2. Show that the set S = {(1, 2), (3, 4)} forms a basis for R²

3. Determine which of the following sets are bases for P₂(R)

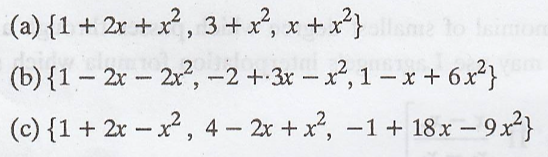
4. Show that the vectors (1, 1, 2), (1, 2, 5), (5, 3, 4) do not form a basis of R³

5. In each part, use the Lagrange interpolation formula to construct the polynomial of smallest degree whose graph contains the following points

(a) (-2, 3), (-1, -6), (1, 0), (3, −2)

(b) (-3, -30), (-2, 7), (0, 15), (1, 10)

6. Prove that any basis {e_i} of V is a linearly independent set.

7. If a vector space V has a basis of n elements then any set of n + 1 vectors is linearly dependent.

8. Let V be a finite dimensional vector space. Then prove that any two bases of V have the same number of elements.