Axioms of Probability

AXIOMS OF PROBABILITY

The probability of an event has been defined, we can collect the assumptions that we have made concerning probabilities into a set of axioms that the probabilities in any random experiment must satisfy.

The axioms do not determine probabilities; the probabilities are assigned based on our knowledge of the system under study. However, the axioms enable us to easily calculate the probabilities of some events from knowledge of the probabilities of other events.

Axioms of probability

Probability is a number that is assigned to each number of a collection of events from a random experiment that satisfies the following properties If S is the sample space and E is any event in a random experiment,

Axiom 1 : 0 = P (E) = 1

Axiom 2 : P (S) = 1

Axiom 3 : For any sequence of mutually exclusive events E₁, E₂, ... (i.e., events for which E_i E_j = φ when i ≠ j),

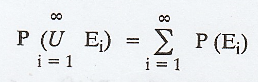
We refer to P (E) as the probability of the event E

Note 1: Axiom 1 states that the probability that the outcome of the experiment is an outcome in E is some number between 0 and 1.

Note 2: Axiom 2 states that, with probability 1, the outcome will be a point in the sample space S.

Note 3: Axiom 3 states that for any sequence of mutually exclusive events the probability of atleast one of these events occurring is just the sum of their respective probabilities.

Theorem 1:

The probability of an impossible event is zero (or) The null event has probability 0 (i.e.,) p (φ) = 0

Proof :

If we consider a sequence of events E₁, E₂, ... where E₁ = S, E_i = φ for i > 1, then the events are mutually exclusive and as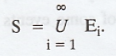 

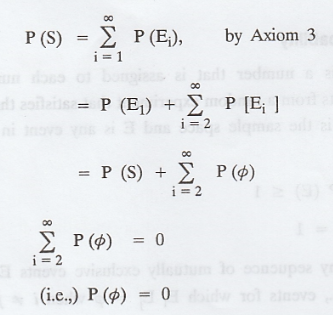
Theorem 2:

If A^C is the complementary event of A, P(A^C) = 1 - P (A) ≤ 1. Proof A and A^C are mutually exclusive events, such that

Theorem 3:

If B C A, P (B) ≤ P (A)

Proof :

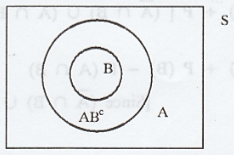
B and A B^C are mutually exclusive events such that

Theorem 4 : Addition law of probability

If A and B are any two events, and are not disjoint, then

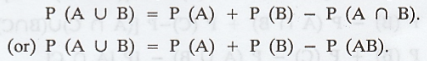
Proof:

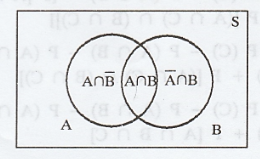
From the venn diagram, we get the events A and Ā ∩ B are disjoint.

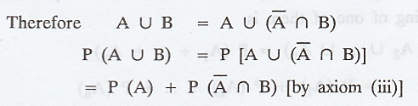
adding and subtracting P(A ∩ B) we get

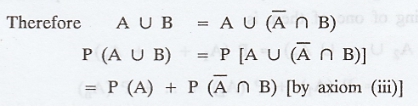
Theorem 5

If A, B and C are any three events then

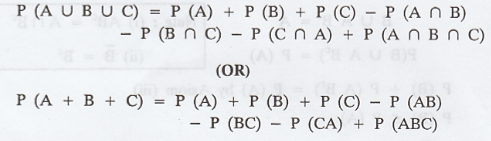
Proof : Using the above result we have

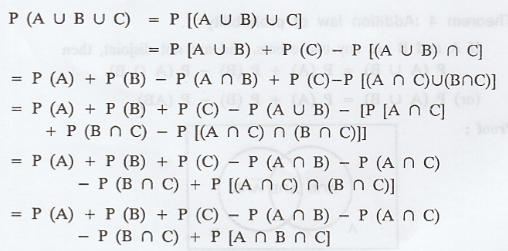
Theorem 6

If A₁, A₂, … A_n are n mutually exclusive events then the probability of the happening of one of them is

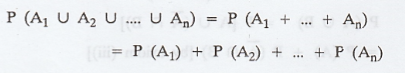
Proof: Let N be the total number of mutually exclusive exhaustive and equally likely cases of which m₁ are favourable to A₁, m₂ are favourable to A₂ and so on.

Probability of occurrence of A₁ = P(A₁) = m₁/N

Probability of occurrence of A₂ = P(A₂) = m₂/N

... ... ... ... ... ... ... ... ... ... ... ...

... ... ... ... ... ... ... ... ... ... ... ...

Probability of occurrence of A_n = P(A_n) = m_n/N

The events being mutually exclusive and equally likely, the number of cases favourable to the event A₁ or A₂ or ... or A_n is m₁ + m₂ + ... + m_n.

.'. The probability of occurrence of one of the events A₁, A₂, ... A_n is

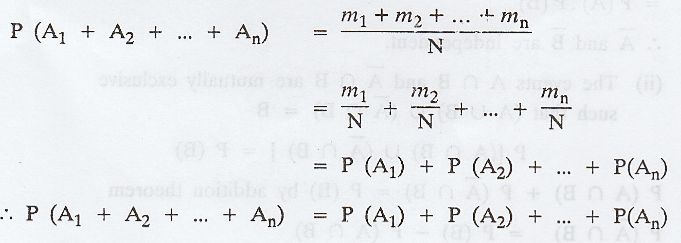
Note: Multiplication theorem :

If two events A and B are independent and can happen simultaneously, the probability of their joint occurrence

P (A ∩ B) = P(A). P(B)

The theorem can be extended to three or more events.

Theorem 7

If the events A and B are independent then

Proof: (i) We know that

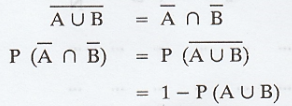
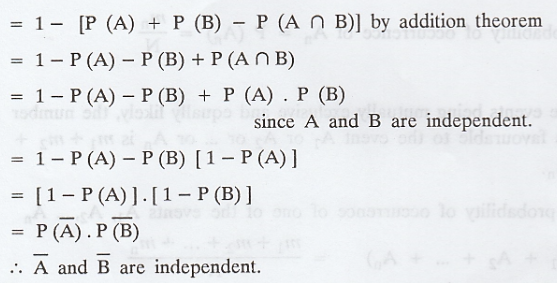
(ii) The events A ∩ B and Ā ∩ B are mutually exclusive such that (A U B) U (Ā ∩ B) = B